2.5.2“边角边”(SAS)-试卷
文档属性
| 名称 | 2.5.2“边角边”(SAS)-试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 1011.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-12 00:00:00 | ||
图片预览


文档简介
2.5.2“边角边”(SAS)
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题8分)
1.如图,????=????,????//????,判定△??????≌△??????的依据是( )
A.SSS B.SAS C.ASA D.HL
/// /
第1题图 第2题图 第3题图 第4题图
2.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D .SSS
3.下列两个三角形的对应元素中,不能判断两个三角形全等的是( )
A、SSA B、AAS C、 SAS D、ASA
4.如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
A.AD=BC B.BD=AC C.∠D=∠C D.OA=AB
5.如图:如果OA=OD,用“SAS”说明△AOB ≌△DOC,还需( )
A.AB=DC B.∠A=∠D C.OB=OC D.∠A=∠E
二.填空题(共4小题,每题5分)
6.如图,根据SAS,如果AB=AC,只要满足____ ,即可判定ΔABD ≌ΔACE。
/ / / /
第6题图 第7题图 第8题图 第9题图
7.把两根钢条A′B、AB′的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳),如图,若得AB=6厘米,则槽宽为_________厘米.
8.如图,已知/,/,要使/≌/,若以“SAS”为依据,补充的条件是_____________
9.如图,已知BD=CD,∠1=∠2;则△ABD≌△ACD,理由是:
___________(已知)
___________(已知)
___________(公共边)
则△ABD≌△ACD(SAS)
三.解答题(共3小题,第10题10分,第11、12题各15分)
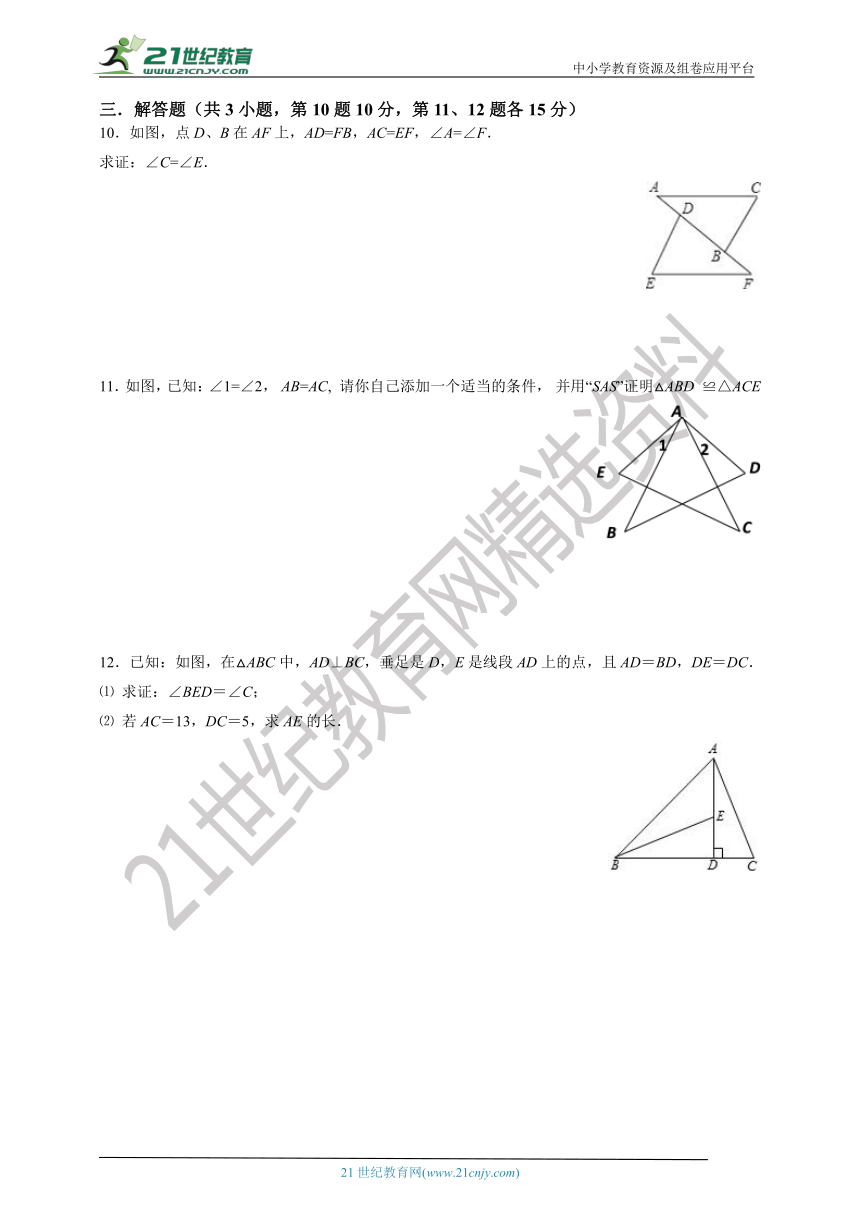
10.如图,点D、B在AF上,AD=FB,AC=EF,∠A=∠F.
求证:∠C=∠E.
/
11.如图,已知:∠1=∠2, AB=AC, 请你自己添加一个适当的条件, 并用“SAS”证明△ABD ≌△ACE
/
12.已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
/
试题解析
/
2.A.
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
3.A
【解析】若有两边一角对应相等时,角必须是两边的夹角.故选A.
4.B
【解析】还需要加上条件BD=AC,
∵在△ABD和△BAC中
,
∴△ACB≌△BDA(SAS),
故选B.
5.C
【解析】根据三角形全等的条件“SAS”,可由对顶角相等,OA=OD可知添加的条件为“OB=OC”.
故选:C.
6.AE=AD
【解析】根据SAS,两边及两边的夹角相等,两三角形全等;
已知AB=AC,∠A为公共角,则另一边为AD=AE。 AB=AC,∠A为两三角形公共角,又AD=AE, ∴△ABD≌△ACE(SAS). 故填AD=AE。
7.6
【解析】如图,连接AB,A′B′,
/
∵在△ABO和△A′B′O中,
,
∴△A′OB′≌△BOA,
∴A′B′=AB=6.
故答案为:6.
8.AC=AE
【解析】由∠BAE=∠DAC,可得∠BAC=∠DAE,添加条件AC=AE,又因为AB=AD,即可利用SAS证明△ABC≌△ADE.
9. BD=CD ∠1=∠2 AD=AD
【解析】在△ABD与△ACD中,
∵BD=CD(已知),
∠1=∠2(已知),
且AD=AD(公关边),
∴△ABD≌△ACD(SAS).
10.见解析.
【解析】由AD=FB易得AB=FD,结合AC=EF,∠A=∠F即可证得△ABC≌△FDE,从而可得∠C=∠E.
解:∵AD=FB,
∴AD+DB=FB+DB,即AB=FD,
又∵AC=EF,∠A=∠F,
∴△ABC≌△FDE,
∴C=∠E.
11.添加条件:AD=AE ,证明见解析
【解析】根据已知一角一边,以及“SAS”可知添加的条件,然后证明即可.
解:∵∠1=∠2
∴∠BAC+∠1=∠CAB+∠2
即∠EAC=∠DAB
在△ABD 和△ACE中:AD=AE,
∠EAC=∠DAB, AB=AC
∴△ABD ≌△ACE (SAS)
12.7
【解析】(1)可以通过证明△ADC≌△BDE可得∠BED=∠C;(2)先根据勾股定理求出AD,由上一问△ADC≌△BDE可得ED=EC,AD=BD,即可求出AE.
解:(1)∵ AD⊥BC, ∴ ∠BDE=∠ADC=90°,
∵在△ADC和△BDE中,
,
∴△ADC≌△BDE,
∴ ∠BED=∠C.
(2)∵ ∠ADC=90°,AC=13,DC=5, ∴AD=12
∵ △BDE≌△ADC, DE=DC=5
∴ AE=AD-DE=12-5=7.
/
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题8分)
1.如图,????=????,????//????,判定△??????≌△??????的依据是( )
A.SSS B.SAS C.ASA D.HL
/// /
第1题图 第2题图 第3题图 第4题图
2.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS B.ASA C.AAS D .SSS
3.下列两个三角形的对应元素中,不能判断两个三角形全等的是( )
A、SSA B、AAS C、 SAS D、ASA
4.如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
A.AD=BC B.BD=AC C.∠D=∠C D.OA=AB
5.如图:如果OA=OD,用“SAS”说明△AOB ≌△DOC,还需( )
A.AB=DC B.∠A=∠D C.OB=OC D.∠A=∠E
二.填空题(共4小题,每题5分)
6.如图,根据SAS,如果AB=AC,只要满足____ ,即可判定ΔABD ≌ΔACE。
/ / / /
第6题图 第7题图 第8题图 第9题图
7.把两根钢条A′B、AB′的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳),如图,若得AB=6厘米,则槽宽为_________厘米.
8.如图,已知/,/,要使/≌/,若以“SAS”为依据,补充的条件是_____________
9.如图,已知BD=CD,∠1=∠2;则△ABD≌△ACD,理由是:
___________(已知)
___________(已知)
___________(公共边)
则△ABD≌△ACD(SAS)
三.解答题(共3小题,第10题10分,第11、12题各15分)
10.如图,点D、B在AF上,AD=FB,AC=EF,∠A=∠F.
求证:∠C=∠E.
/
11.如图,已知:∠1=∠2, AB=AC, 请你自己添加一个适当的条件, 并用“SAS”证明△ABD ≌△ACE
/
12.已知:如图,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.
⑴ 求证:∠BED=∠C;
⑵ 若AC=13,DC=5,求AE的长.
/
试题解析
/
2.A.
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
3.A
【解析】若有两边一角对应相等时,角必须是两边的夹角.故选A.
4.B
【解析】还需要加上条件BD=AC,
∵在△ABD和△BAC中
,
∴△ACB≌△BDA(SAS),
故选B.
5.C
【解析】根据三角形全等的条件“SAS”,可由对顶角相等,OA=OD可知添加的条件为“OB=OC”.
故选:C.
6.AE=AD
【解析】根据SAS,两边及两边的夹角相等,两三角形全等;
已知AB=AC,∠A为公共角,则另一边为AD=AE。 AB=AC,∠A为两三角形公共角,又AD=AE, ∴△ABD≌△ACE(SAS). 故填AD=AE。
7.6
【解析】如图,连接AB,A′B′,
/
∵在△ABO和△A′B′O中,
,
∴△A′OB′≌△BOA,
∴A′B′=AB=6.
故答案为:6.
8.AC=AE
【解析】由∠BAE=∠DAC,可得∠BAC=∠DAE,添加条件AC=AE,又因为AB=AD,即可利用SAS证明△ABC≌△ADE.
9. BD=CD ∠1=∠2 AD=AD
【解析】在△ABD与△ACD中,
∵BD=CD(已知),
∠1=∠2(已知),
且AD=AD(公关边),
∴△ABD≌△ACD(SAS).
10.见解析.
【解析】由AD=FB易得AB=FD,结合AC=EF,∠A=∠F即可证得△ABC≌△FDE,从而可得∠C=∠E.
解:∵AD=FB,
∴AD+DB=FB+DB,即AB=FD,
又∵AC=EF,∠A=∠F,
∴△ABC≌△FDE,
∴C=∠E.
11.添加条件:AD=AE ,证明见解析
【解析】根据已知一角一边,以及“SAS”可知添加的条件,然后证明即可.
解:∵∠1=∠2
∴∠BAC+∠1=∠CAB+∠2
即∠EAC=∠DAB
在△ABD 和△ACE中:AD=AE,
∠EAC=∠DAB, AB=AC
∴△ABD ≌△ACE (SAS)
12.7
【解析】(1)可以通过证明△ADC≌△BDE可得∠BED=∠C;(2)先根据勾股定理求出AD,由上一问△ADC≌△BDE可得ED=EC,AD=BD,即可求出AE.
解:(1)∵ AD⊥BC, ∴ ∠BDE=∠ADC=90°,
∵在△ADC和△BDE中,
,
∴△ADC≌△BDE,
∴ ∠BED=∠C.
(2)∵ ∠ADC=90°,AC=13,DC=5, ∴AD=12
∵ △BDE≌△ADC, DE=DC=5
∴ AE=AD-DE=12-5=7.
/
同课章节目录
