组合图形的面积课件 (共35张PPT)
文档属性
| 名称 | 组合图形的面积课件 (共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 850.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-11 21:18:00 | ||
图片预览






文档简介
课件35张PPT。第 4 课时 组合图形的面积6 多边形的面积RJ 五年级上册 (1)认识组合图形
(2)组合图形面积的计算课后作业探索新知课堂总结当堂检测游戏导入猜一猜,里面都有哪些平面图形?长方形面积=长×宽S=ab正方形面积
=边长×边长S=a2平行四边形的面积
=底×高
S=ah三角形的面积
=底×高÷2
S=ah ÷2梯形的面积
=(上底+下底) × 高÷2
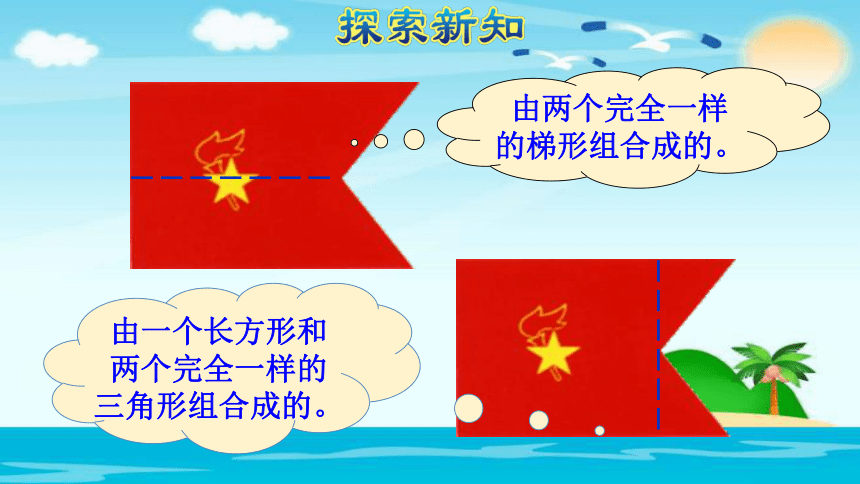
S=(a+b) ×h ÷2认识组合图形你能在我们的周围找一找组合图形吗?什么是组合图形?由几个简单的图形组合而成的图形叫组合图形。 这些组合图形是由哪些简单图形组成的?与同桌互相说一说。由两个完全一样的梯形组合成的。由一个长方形和两个完全一样的三角形组合成的。一个长方形去掉一个三角形而得到的图形。分割法添补法归纳总结:组合图形是由几个简单的图形组合而成的。用“分割法”和“添补法”可以把组合图形转化成几个简单的图形。组合图形面积的计算 右图表示的是一间房子侧面墙的形状。它的面积是多少平方米? 自学提示:
1.你能用自己喜欢的方法求出它的面积吗?
2.可以在图上画出你的思路,然后再求出面积,看谁的方法最多;
3.如果有困难可以两个人一起研究;方法一:三角形+正方形三角形面积=5×2÷2=5(m2)
正方形面积=5×5 = 25(cm2)
房子侧面面积=25+5 =30(cm2)方法二:两个梯形梯形面积=(5+2+5)×(5÷2)÷2
=12×2.5÷2
=30÷2
=15(m2)
房子侧面面积=15×2=30(cm2)方法三:拼成一个长方形长方形面积=(5+2+5)×(5÷2)
=12×2.5
=30(m2)
房子侧面面积=长方形面积方法四:从长方形中挖走两个小三角形长方形面积=(5+2)×5
=7×5
=35(m2)
两个三角形面积=5×2÷2=5(m2)
房子侧面面积=35-5=30(cm2)方法一方法二方法三方法四对比归纳: 1.以上四种方法,有什么相同点?
2.你更喜欢哪一种方法?为什么?
3.你能结合此题说一说,在求组合图形面积时应怎么做?归纳总结:求组合图形面积的方法:
观察、分析组合图形可分割或添补哪些学过的基本图形,再找出计算基本图形面积需要的条件,然后利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。4.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米? (选题源于教材P101第4题) (70+40)×30÷2-30×15
=110×30÷2-450
=3300÷2-450
=1650-450
=1200(m2)
答:草地的面积是1200平方米。5.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?(选题源于教材P101练习二十二第5题)(2+10)×12÷2-3×4÷2-(4+6)×4÷2=46(cm2)
答:它的面积是46cm2。1.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。2.用分割法计算下面图形的面积。(单位:厘米)
(2)
4×1.5÷2+4×2÷2=7(平方厘米)(10+16)×12÷2=156(平方厘米)10×16÷2=80(平方厘米)156+80=236(平方厘米)(3)
(4)
(25-10)×(10+10)÷2+10×10=250(平方厘米)20×10=200(平方厘米)20×8=160(平方厘米) 200+160=360(平方厘米)3.用添补法计算组合图形的面积。(单位:厘米)15×8-3×2=114(平方厘米)(10+10+5)×10÷2-6×8÷2=101(平方厘米)(3)
(4)
13×20-12×5÷2=230(平方厘米)(10+20)×22÷2-8×6÷2=306(平方厘米)4.求下面各图中阴影部分的面积。(单位:厘米) (2)
8×6÷2+6×6
÷2=42(平方厘米)8×8+12×12=208(平方厘米)(8+12)×12÷2=120(平方厘米)(12-8)×12÷2=24(平方厘米)8×8÷2=32(平方厘米)208-32-120-24=32(平方厘米)5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)方法一:3×4+(4+10)×(8-3)÷2=12+35=47(平方厘米)方法二:8×4+(8-3)×(10-4)÷2=32+15=47(平方厘米)5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)方法三:8×10-(8+3)×(10-4)÷2=80-33=47(平方厘米)方法四:(8+3)×4÷2+(8-3)×10÷2=22+25=47(平方厘米)求组合图形面积的基本步骤和方法:观察、分析组合图形可分割或添补成哪些已学过的基本图形。
找出计算基本图形面积需要的条件。
利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。课件PPT谢谢请领导老师批评指正
=边长×边长S=a2平行四边形的面积
=底×高
S=ah三角形的面积
=底×高÷2
S=ah ÷2梯形的面积
=(上底+下底) × 高÷2
S=(a+b) ×h ÷2认识组合图形你能在我们的周围找一找组合图形吗?什么是组合图形?由几个简单的图形组合而成的图形叫组合图形。 这些组合图形是由哪些简单图形组成的?与同桌互相说一说。由两个完全一样的梯形组合成的。由一个长方形和两个完全一样的三角形组合成的。一个长方形去掉一个三角形而得到的图形。分割法添补法归纳总结:组合图形是由几个简单的图形组合而成的。用“分割法”和“添补法”可以把组合图形转化成几个简单的图形。组合图形面积的计算 右图表示的是一间房子侧面墙的形状。它的面积是多少平方米? 自学提示:
1.你能用自己喜欢的方法求出它的面积吗?
2.可以在图上画出你的思路,然后再求出面积,看谁的方法最多;
3.如果有困难可以两个人一起研究;方法一:三角形+正方形三角形面积=5×2÷2=5(m2)
正方形面积=5×5 = 25(cm2)
房子侧面面积=25+5 =30(cm2)方法二:两个梯形梯形面积=(5+2+5)×(5÷2)÷2
=12×2.5÷2
=30÷2
=15(m2)
房子侧面面积=15×2=30(cm2)方法三:拼成一个长方形长方形面积=(5+2+5)×(5÷2)
=12×2.5
=30(m2)
房子侧面面积=长方形面积方法四:从长方形中挖走两个小三角形长方形面积=(5+2)×5
=7×5
=35(m2)
两个三角形面积=5×2÷2=5(m2)
房子侧面面积=35-5=30(cm2)方法一方法二方法三方法四对比归纳: 1.以上四种方法,有什么相同点?
2.你更喜欢哪一种方法?为什么?
3.你能结合此题说一说,在求组合图形面积时应怎么做?归纳总结:求组合图形面积的方法:
观察、分析组合图形可分割或添补哪些学过的基本图形,再找出计算基本图形面积需要的条件,然后利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。4.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米? (选题源于教材P101第4题) (70+40)×30÷2-30×15
=110×30÷2-450
=3300÷2-450
=1650-450
=1200(m2)
答:草地的面积是1200平方米。5.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?(选题源于教材P101练习二十二第5题)(2+10)×12÷2-3×4÷2-(4+6)×4÷2=46(cm2)
答:它的面积是46cm2。1.下面组合图形可以分成哪些已学过的图形?请你在图中画一画。2.用分割法计算下面图形的面积。(单位:厘米)
(2)
4×1.5÷2+4×2÷2=7(平方厘米)(10+16)×12÷2=156(平方厘米)10×16÷2=80(平方厘米)156+80=236(平方厘米)(3)
(4)
(25-10)×(10+10)÷2+10×10=250(平方厘米)20×10=200(平方厘米)20×8=160(平方厘米) 200+160=360(平方厘米)3.用添补法计算组合图形的面积。(单位:厘米)15×8-3×2=114(平方厘米)(10+10+5)×10÷2-6×8÷2=101(平方厘米)(3)
(4)
13×20-12×5÷2=230(平方厘米)(10+20)×22÷2-8×6÷2=306(平方厘米)4.求下面各图中阴影部分的面积。(单位:厘米) (2)
8×6÷2+6×6
÷2=42(平方厘米)8×8+12×12=208(平方厘米)(8+12)×12÷2=120(平方厘米)(12-8)×12÷2=24(平方厘米)8×8÷2=32(平方厘米)208-32-120-24=32(平方厘米)5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)方法一:3×4+(4+10)×(8-3)÷2=12+35=47(平方厘米)方法二:8×4+(8-3)×(10-4)÷2=32+15=47(平方厘米)5.用不同的方法计算下图的面积。(单位:厘米)(用四种方法)方法三:8×10-(8+3)×(10-4)÷2=80-33=47(平方厘米)方法四:(8+3)×4÷2+(8-3)×10÷2=22+25=47(平方厘米)求组合图形面积的基本步骤和方法:观察、分析组合图形可分割或添补成哪些已学过的基本图形。
找出计算基本图形面积需要的条件。
利用合理的方法,先计算出基本图形的面积,再利用基本图形的面积和或差计算出组合图形的面积。课件PPT谢谢请领导老师批评指正
