2.5直线和圆的位置关系同步测试卷(附答案)
文档属性
| 名称 | 2.5直线和圆的位置关系同步测试卷(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-12 11:28:12 | ||
图片预览



文档简介
九年级数学2.5《直线和圆的位置关系》同步测试
一、选择题:
1、在中,,,周长为12,那么的内切圆半径为( )
A. 3 B. 2. C. 2 D. 1
2、(2018?泰安)如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
3、下列命题是真命题的是( )
A.垂直于圆的半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.直线上一点到圆心的距离等于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
4、 直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A. r<6 B. r=6 C. r>6 D. r≥6
5、(2018?上海)如图,已知∠POQ=30°,点A、B在射线OQ上(点A在点O、B之间),半径长为2的⊙A与直线OP相切,半径长为3的⊙B与⊙A相交,那么OB的取值范围是( )
A.5<OB<9 B.4<OB<9 C.3<OB<7 D.2<OB<7
6、已知圆的半径为6.5cm,圆心到直线的距离为4.5cm,那么这条直线和这个圆的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
7、如图,AB、AC切⊙O于B、C,AO交⊙O于D,过D作⊙O切线分别交AB、AC于E、F,若,,则△AEF的周长是( )
A. 10 B. 12 C. 14 D. 16
8、 如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 无法确定
9、如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据,这扇圆弧形门所在的圆与水平地面是相切的,m,m,且,与水平地面都是垂直的.根据以上数据,请你帮小红计算这扇圆弧形门的最高点离地面的距离是( )
A. 2 m B. 2.5 m C. 2.4 m D. 2.1 m
10、(2018?湘西州)已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
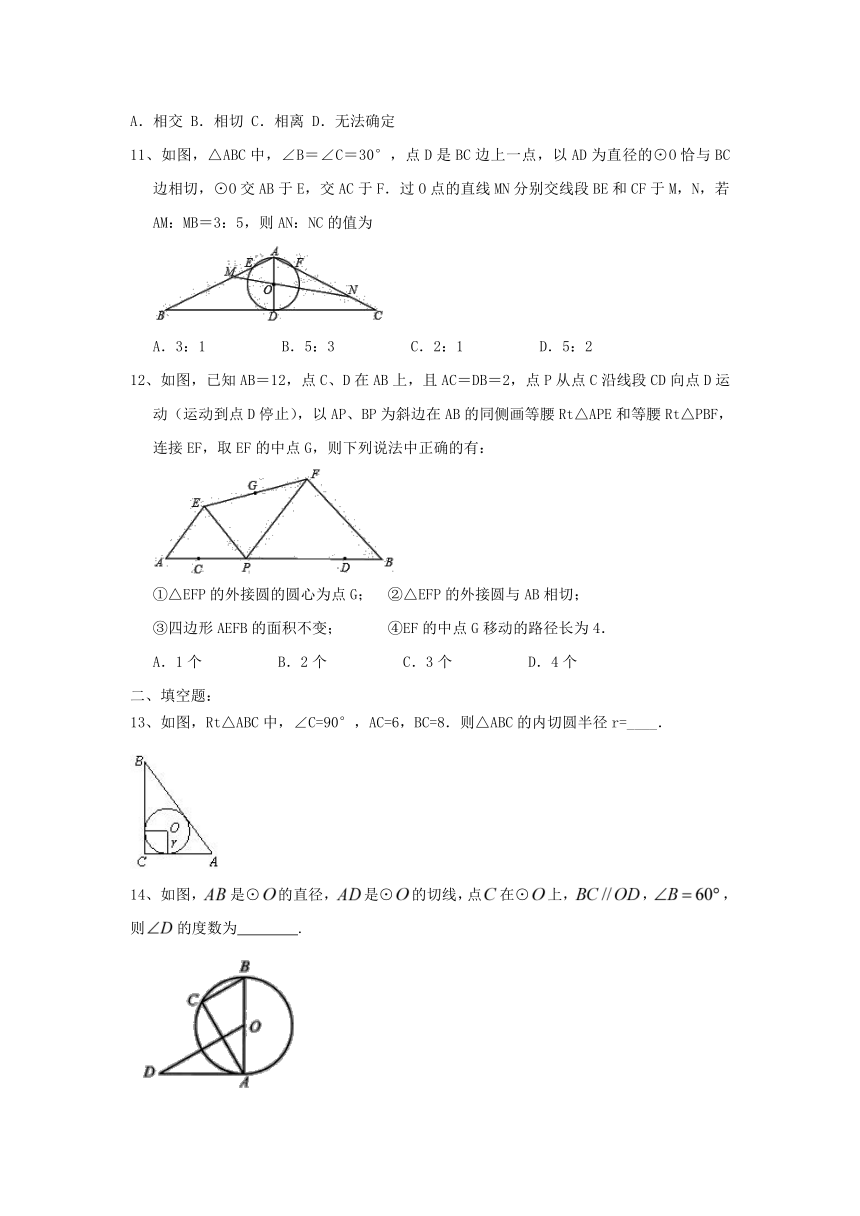
11、如图,△ABC中,∠B=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AM:MB=3:5,则AN:NC的值为
A.3:1 B.5:3 C.2:1 D.5:2
12、如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有:
①△EFP的外接圆的圆心为点G; ②△EFP的外接圆与AB相切;
③四边形AEFB的面积不变; ④EF的中点G移动的路径长为4.
A.1个 B.2个 C.3个 D.4个
二、填空题:
13、如图,Rt△ABC中,∠C=90°,AC=6,BC=8.则△ABC的内切圆半径r=____.
14、如图,是⊙的直径,是⊙的切线,点在⊙上,,,则的度数为 .
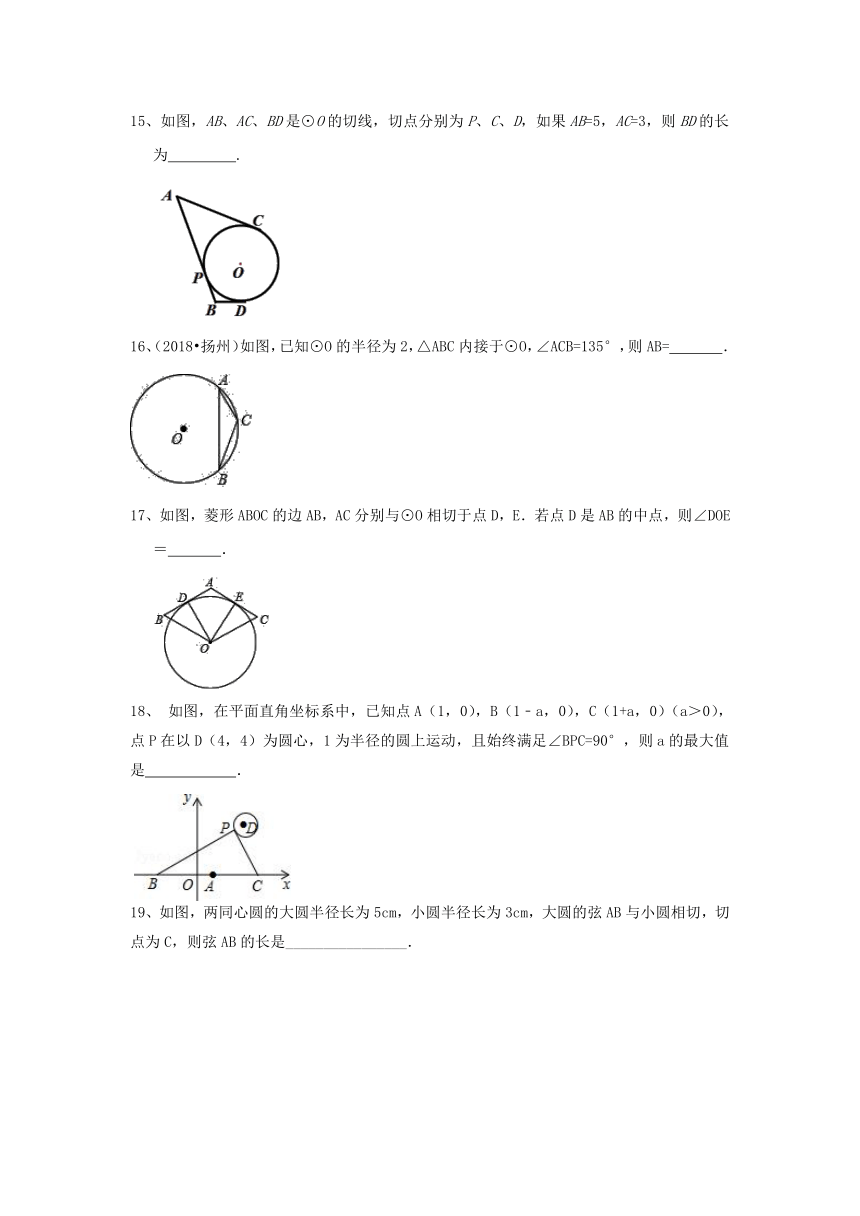
15、如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D,如果AB=5,AC=3,则BD的长为 .
16、(2018?扬州)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB= .
17、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= .
18、 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
19、如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是________________.
20、如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD?BC=9,则直径AB的长为 .
21、(2018?内江)已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4+10b,则△ABC的外接圆半径= .
22、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是____
三、解答题:
23、如图,是⊙的直径,为⊙上一点,过上一点作⊙的切线,且于点.
(1)若,求的度数;
(2)若⊙的半径为2 ,,求的长.
24、如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,E为BC的中点,连接DE.
(1)求证:DE为⊙O的切线;
(2)如果⊙O的半径为3,ED=4,延长EO交⊙O于F,连接DF,与OA交于点G,求OG的长.
25、(2018?温州)如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在BD上.
(1)求证:AE=AB.
(2)若∠CAB=90°,cos∠ADB=,BE=2,求BC的长.
26、射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,cm,cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切,请写出可取的所有值_________
27、(2018?泰州)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
答案:
一、选择题:
1、D
2、C
3、D
4、C
5、A
6、C
7、D
8、A
9、B
10、B
11、A
12、B
二、填空题:
13、2
14、30°
15、2
16、2
17、60°
18、6
19、8cm
20、6
21、25/8
22、8<AB≤10
三、解答题:
23、(1) 的度数为65°;
(2) =2.
24、OG=15/11
25、(1)由折叠的性质可知,△ADE≌△ADC,
∴∠AED=∠ACD,AE=AC,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB;
(2)如图,过A作AH⊥BE于点H,
∵AB=AE,BE=2,
∴BH=EH=1,
∵∠ABE=∠AEB=∠ADB,cos∠ADB=,
∴cos∠ABE=cos∠ADB=,
∴=.
∴AC=AB=3,
∵∠BAC=90°,AC=AB,
∴BC=3.
26、∵是等边三角形,
∴,,
∵,.
∴N为BC中点,
∴,,
分为三种情况:①如图1,
当⊙P切AB于M′时,连接PM′,
则,,
∵,
∴,,
∴,
即;
②如图2,
当⊙P于AC切于A点时,连接PA,
则,,,
∴,
∴,
即,
当⊙P于AC切于C点时,连接P′C,
则,,,
∴,
∴,
即当时,⊙P和AC边相切;
③如图3,
当⊙P切BC于N′时,连接PN′
则,,
∵,
∴,,
∴,
即;
故答案为:或或.
27、(1)DE与⊙O相切,
理由:连接DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)∵∠ABC的平分线交⊙O于点D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3,
∴BD==6,
∵sin∠DBF==,
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°===,
∴DO=2,
则FO=,
故图中阴影部分的面积为:﹣××3=2π﹣.
C
O
F
A
E
D
B
一、选择题:
1、在中,,,周长为12,那么的内切圆半径为( )
A. 3 B. 2. C. 2 D. 1
2、(2018?泰安)如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
3、下列命题是真命题的是( )
A.垂直于圆的半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.直线上一点到圆心的距离等于圆的半径的直线是圆的切线
D.到圆心的距离等于圆的半径的直线是圆的切线
4、 直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A. r<6 B. r=6 C. r>6 D. r≥6
5、(2018?上海)如图,已知∠POQ=30°,点A、B在射线OQ上(点A在点O、B之间),半径长为2的⊙A与直线OP相切,半径长为3的⊙B与⊙A相交,那么OB的取值范围是( )
A.5<OB<9 B.4<OB<9 C.3<OB<7 D.2<OB<7
6、已知圆的半径为6.5cm,圆心到直线的距离为4.5cm,那么这条直线和这个圆的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
7、如图,AB、AC切⊙O于B、C,AO交⊙O于D,过D作⊙O切线分别交AB、AC于E、F,若,,则△AEF的周长是( )
A. 10 B. 12 C. 14 D. 16
8、 如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 无法确定
9、如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,她了解到这扇门的相关数据,这扇圆弧形门所在的圆与水平地面是相切的,m,m,且,与水平地面都是垂直的.根据以上数据,请你帮小红计算这扇圆弧形门的最高点离地面的距离是( )
A. 2 m B. 2.5 m C. 2.4 m D. 2.1 m
10、(2018?湘西州)已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
11、如图,△ABC中,∠B=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AM:MB=3:5,则AN:NC的值为
A.3:1 B.5:3 C.2:1 D.5:2
12、如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,则下列说法中正确的有:
①△EFP的外接圆的圆心为点G; ②△EFP的外接圆与AB相切;
③四边形AEFB的面积不变; ④EF的中点G移动的路径长为4.
A.1个 B.2个 C.3个 D.4个
二、填空题:
13、如图,Rt△ABC中,∠C=90°,AC=6,BC=8.则△ABC的内切圆半径r=____.
14、如图,是⊙的直径,是⊙的切线,点在⊙上,,,则的度数为 .
15、如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D,如果AB=5,AC=3,则BD的长为 .
16、(2018?扬州)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB= .
17、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= .
18、 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
19、如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是________________.
20、如图,AB是⊙O的直径,AM和BN是它的两条切线,DC切⊙O于E,交AM于D,交BN于C.若AD?BC=9,则直径AB的长为 .
21、(2018?内江)已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4+10b,则△ABC的外接圆半径= .
22、如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是____
三、解答题:
23、如图,是⊙的直径,为⊙上一点,过上一点作⊙的切线,且于点.
(1)若,求的度数;
(2)若⊙的半径为2 ,,求的长.
24、如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,E为BC的中点,连接DE.
(1)求证:DE为⊙O的切线;
(2)如果⊙O的半径为3,ED=4,延长EO交⊙O于F,连接DF,与OA交于点G,求OG的长.
25、(2018?温州)如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在BD上.
(1)求证:AE=AB.
(2)若∠CAB=90°,cos∠ADB=,BE=2,求BC的长.
26、射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,cm,cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切,请写出可取的所有值_________
27、(2018?泰州)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
答案:
一、选择题:
1、D
2、C
3、D
4、C
5、A
6、C
7、D
8、A
9、B
10、B
11、A
12、B
二、填空题:
13、2
14、30°
15、2
16、2
17、60°
18、6
19、8cm
20、6
21、25/8
22、8<AB≤10
三、解答题:
23、(1) 的度数为65°;
(2) =2.
24、OG=15/11
25、(1)由折叠的性质可知,△ADE≌△ADC,
∴∠AED=∠ACD,AE=AC,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB;
(2)如图,过A作AH⊥BE于点H,
∵AB=AE,BE=2,
∴BH=EH=1,
∵∠ABE=∠AEB=∠ADB,cos∠ADB=,
∴cos∠ABE=cos∠ADB=,
∴=.
∴AC=AB=3,
∵∠BAC=90°,AC=AB,
∴BC=3.
26、∵是等边三角形,
∴,,
∵,.
∴N为BC中点,
∴,,
分为三种情况:①如图1,
当⊙P切AB于M′时,连接PM′,
则,,
∵,
∴,,
∴,
即;
②如图2,
当⊙P于AC切于A点时,连接PA,
则,,,
∴,
∴,
即,
当⊙P于AC切于C点时,连接P′C,
则,,,
∴,
∴,
即当时,⊙P和AC边相切;
③如图3,
当⊙P切BC于N′时,连接PN′
则,,
∵,
∴,,
∴,
即;
故答案为:或或.
27、(1)DE与⊙O相切,
理由:连接DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)∵∠ABC的平分线交⊙O于点D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3,
∴BD==6,
∵sin∠DBF==,
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°===,
∴DO=2,
则FO=,
故图中阴影部分的面积为:﹣××3=2π﹣.
C
O
F
A
E
D
B
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
