人教版九年级上数学 22.1.5 二次函数的解析式的三种形式课件(共26张ppt)
文档属性
| 名称 | 人教版九年级上数学 22.1.5 二次函数的解析式的三种形式课件(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-12 18:51:34 | ||
图片预览


文档简介
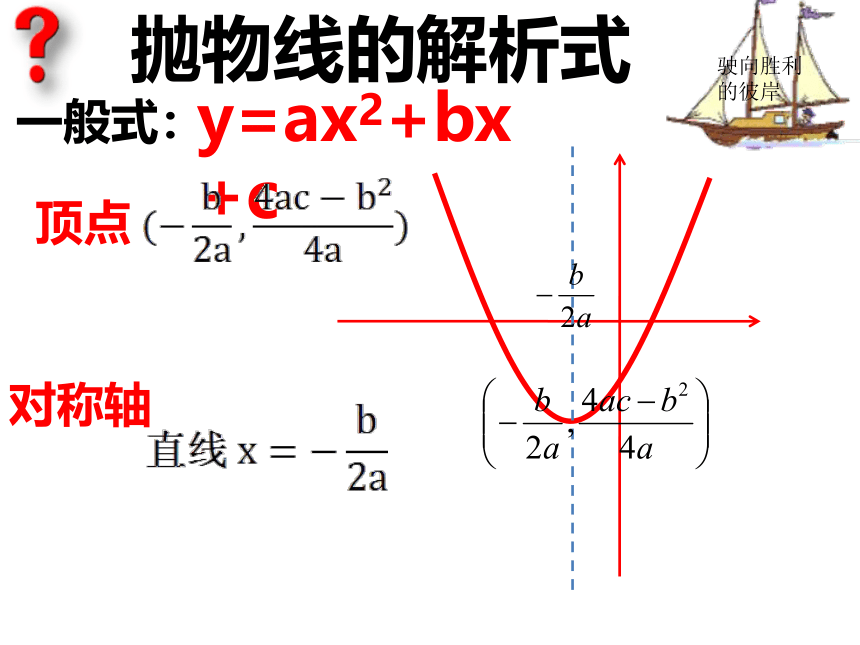
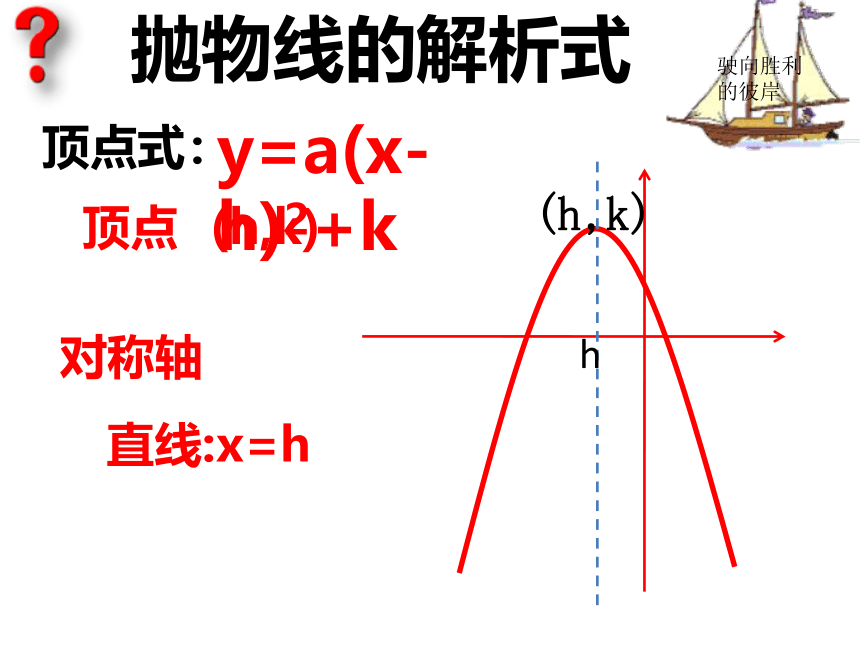
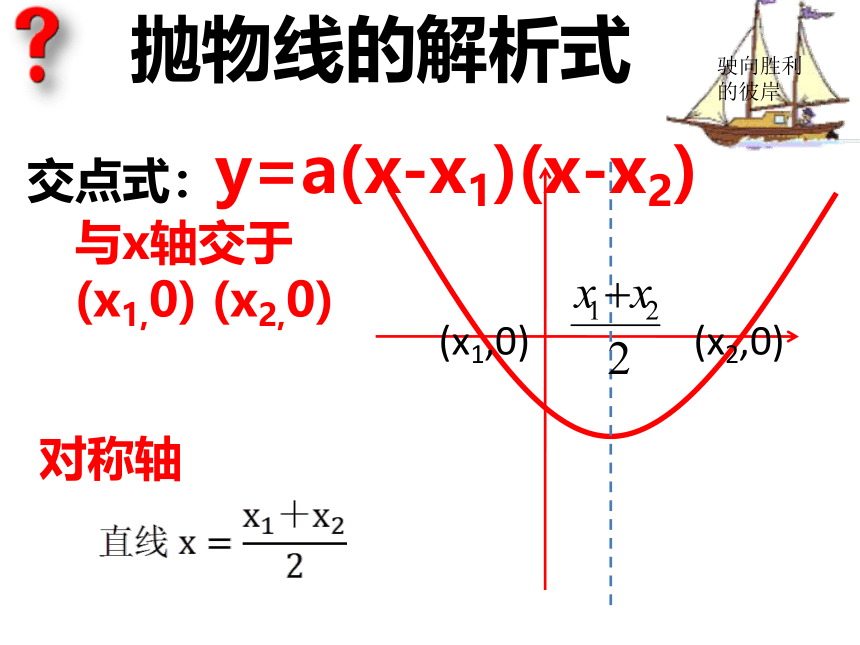
课件26张PPT。抛物线的解析式抛物线的解析式一般式:y=ax2+bx+c顶点对称轴抛物线的解析式顶点式:y=a(x-h)2+k(h,k)直线:x=h 顶点对称轴h(h,k)抛物线的解析式交点式:y=a(x-x1)(x-x2)对称轴与x轴交于
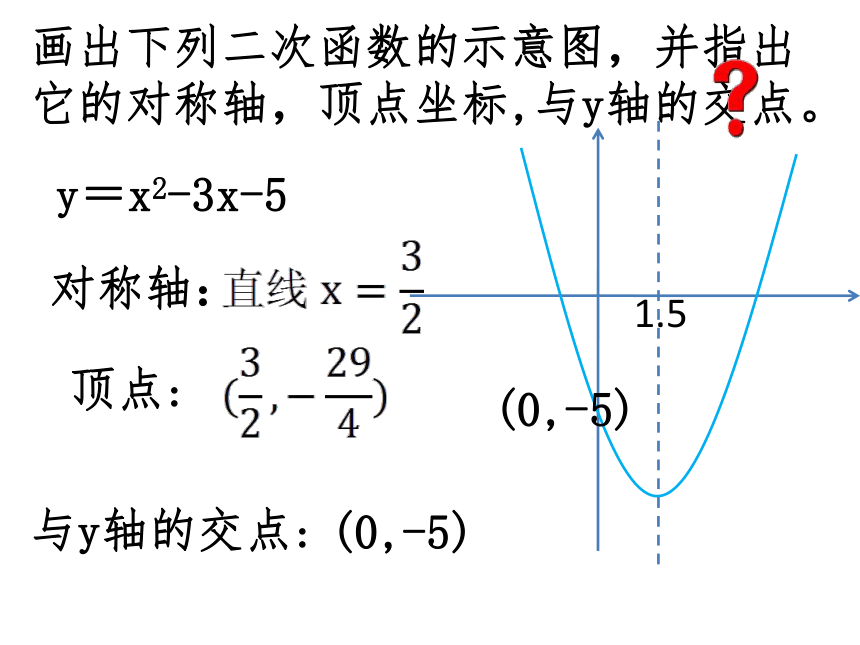
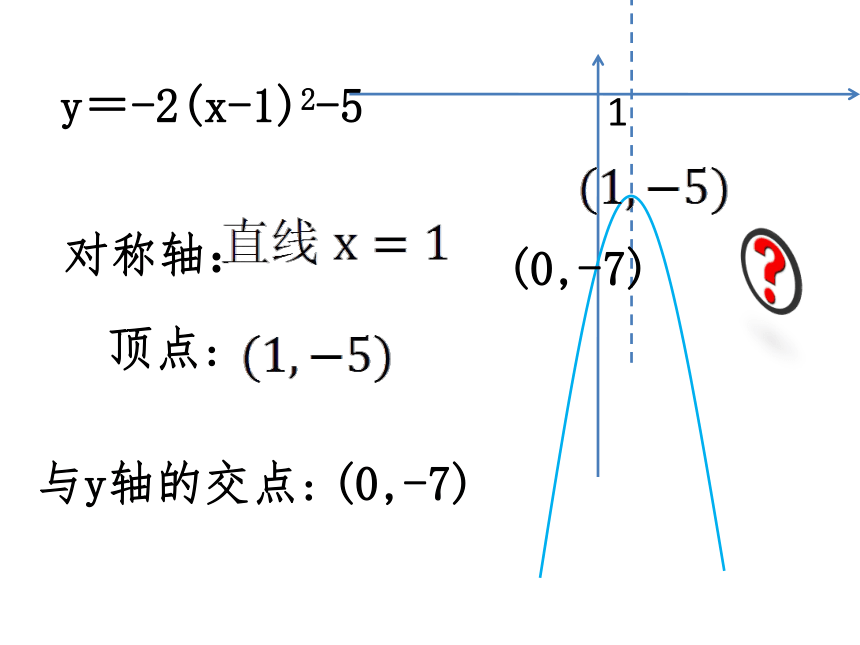
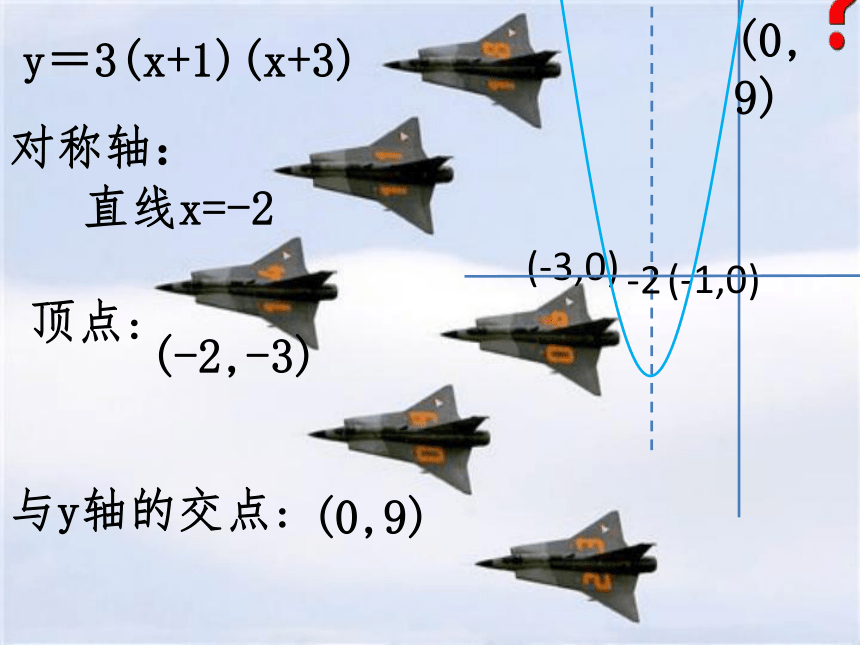
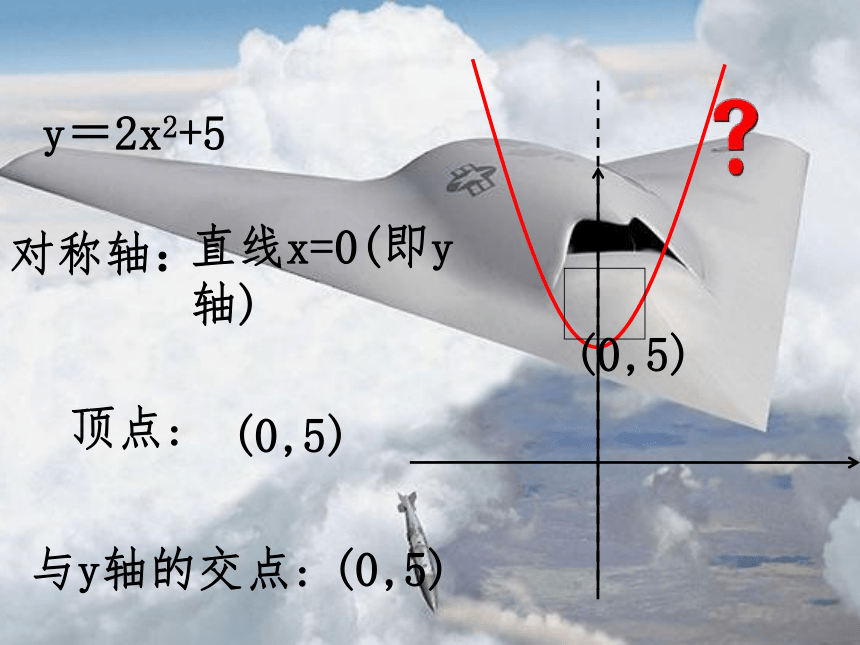
(x1,0) (x2,0)(x1,0)(x2,0)画出下列二次函数的示意图,并指出它的对称轴,顶点坐标,与y轴的交点。y=x2-3x-5对称轴:顶点:与y轴的交点:(0,-5)(0,-5)y=0.5(x-1)(x+3)-1对称轴:顶点:与y轴的交点:(0,-1.5)(-3,0)(1,0)(0,-1.5)(-1,-2)y=-2(x-1)2-5对称轴:顶点:与y轴的交点:(0,-7)(0,-7)y=3(x+1)(x+3)-2对称轴:顶点:与y轴的交点:(0,9)(-3,0)(-1,0)(0,9)(-2,-3)直线x=-2y=2x2+5对称轴:顶点:与y轴的交点:(0,5)(0,5)直线x=0(即y轴)(0,5)y=-2(x+2)(x-3)0.5对称轴:顶点:与y轴的交点:(0,12)(-2, 0)(3,0)(0,12)直线x=0.5y=2(x+1)2-1对称轴:顶点:与y轴的交点:(0,2)(0,2)(-1,0)直线x=-1y=-2(x-1)(x-3)2对称轴:顶点:与y轴的交点:(0,-6)(3,0)(1,0)(0,-6)(2,2)直线x=2y=-3(x-3)23对称轴:顶点:与y轴的交点:(0,-27)(3,0)(0,-27)(3,0)直线x=3y=-(x+3)2+1-3对称轴:顶点:与y轴的交点:(0,-8)(-3,1)(0,-8)(-3,1)直线x=-3y=-2(x+2)(x-4)1对称轴:顶点:与y轴的交点:(0,16)(4,0)(-2,0)(0,16)(1,18)直线x=1 1.已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和点(5,0),则该抛物线的解析式为 .2.求满足下列条件的二次函数解析式:
(1)二次函数的图像与x轴交于点A(2,0),
B(4,0),且图像过点C(1,6)
(2)二次函数当x=1时有最大值y=4,且x=0时
y=0
(3)二次函数的图像可由函数y=ax2-1的图像
向左平移2个单位得到,且过点M(-1,-3)
已知抛物线 ,
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小已知抛物线 ,
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小(m≠0)已知抛物线y=ax2+bx+c的称轴是:直线x=1
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小如图是抛物线y=ax2+bx+c-1试判断:
a 0, b 0, c 0,
a+b+c 0,
a-b+c 0,
2a-b 0,
2a+b 0,
如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
a-b+c 0,
b2-4ac 0,
2a+b 0, 如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,
2a+b 0,
2a-b 0,如图是抛物线y=ax2+bx+c1试判断:
ac 0,
A+b+c 0,
b2-4ac 0,
2a+b 0,
4a+2b+c c
如图是抛物线y=ax2+bx+c试判断:
a 0, b 0,
c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,
2a+b 0,
(x1,0) (x2,0)(x1,0)(x2,0)画出下列二次函数的示意图,并指出它的对称轴,顶点坐标,与y轴的交点。y=x2-3x-5对称轴:顶点:与y轴的交点:(0,-5)(0,-5)y=0.5(x-1)(x+3)-1对称轴:顶点:与y轴的交点:(0,-1.5)(-3,0)(1,0)(0,-1.5)(-1,-2)y=-2(x-1)2-5对称轴:顶点:与y轴的交点:(0,-7)(0,-7)y=3(x+1)(x+3)-2对称轴:顶点:与y轴的交点:(0,9)(-3,0)(-1,0)(0,9)(-2,-3)直线x=-2y=2x2+5对称轴:顶点:与y轴的交点:(0,5)(0,5)直线x=0(即y轴)(0,5)y=-2(x+2)(x-3)0.5对称轴:顶点:与y轴的交点:(0,12)(-2, 0)(3,0)(0,12)直线x=0.5y=2(x+1)2-1对称轴:顶点:与y轴的交点:(0,2)(0,2)(-1,0)直线x=-1y=-2(x-1)(x-3)2对称轴:顶点:与y轴的交点:(0,-6)(3,0)(1,0)(0,-6)(2,2)直线x=2y=-3(x-3)23对称轴:顶点:与y轴的交点:(0,-27)(3,0)(0,-27)(3,0)直线x=3y=-(x+3)2+1-3对称轴:顶点:与y轴的交点:(0,-8)(-3,1)(0,-8)(-3,1)直线x=-3y=-2(x+2)(x-4)1对称轴:顶点:与y轴的交点:(0,16)(4,0)(-2,0)(0,16)(1,18)直线x=1 1.已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和点(5,0),则该抛物线的解析式为 .2.求满足下列条件的二次函数解析式:
(1)二次函数的图像与x轴交于点A(2,0),
B(4,0),且图像过点C(1,6)
(2)二次函数当x=1时有最大值y=4,且x=0时
y=0
(3)二次函数的图像可由函数y=ax2-1的图像
向左平移2个单位得到,且过点M(-1,-3)
已知抛物线 ,
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小已知抛物线 ,
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小(m≠0)已知抛物线y=ax2+bx+c的称轴是:直线x=1
点A(-1,y1), B(1,y2), C(2,y3)在这条抛物线上,比较y1,y2,y3的大小如图是抛物线y=ax2+bx+c-1试判断:
a 0, b 0, c 0,
a+b+c 0,
a-b+c 0,
2a-b 0,
2a+b 0,
如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
a-b+c 0,
b2-4ac 0,
2a+b 0, 如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,
2a+b 0,
2a-b 0,如图是抛物线y=ax2+bx+c1试判断:
ac 0,
A+b+c 0,
b2-4ac 0,
2a+b 0,
4a+2b+c c
如图是抛物线y=ax2+bx+c试判断:
a 0, b 0,
c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,如图是抛物线y=ax2+bx+c1试判断:
a 0, b 0, c 0,
a+b+c 0,
4a-2b+c 0
b2-4ac 0,
2a+b 0,
同课章节目录
