苏科版数学八年级上《第2章轴对称图形》提优测试(含简略答案)
文档属性
| 名称 | 苏科版数学八年级上《第2章轴对称图形》提优测试(含简略答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-13 00:00:00 | ||
图片预览

文档简介
第2章《轴对称图形》国庆提优测试
(满分:100分 时间:90分钟)
一、选择题(每题3分,共24分)
1.观察下列各组图形,其中不是轴对称的是( )
2.把一张长方形纸片按如图①、②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
3.如图,在由相同的小正方形组成的的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形构成的图形为轴对称图形,则还需要涂黑的小正方形的序号是( )
A.①或② B.③或⑥或⑦
C.④或⑤ D.③或⑨
4.如图,平分,且.若点、分别在、上,且为等边三角形,则满足上述条件的有( )
A. 2个 B. 3个 C. 4个 D.无数个
5.如图,、分别是、平分线上的点,于点,于点,于点,则下列结论错误的是( )
A.
B.
C. 与互佘的角有2个
D. 是的中点
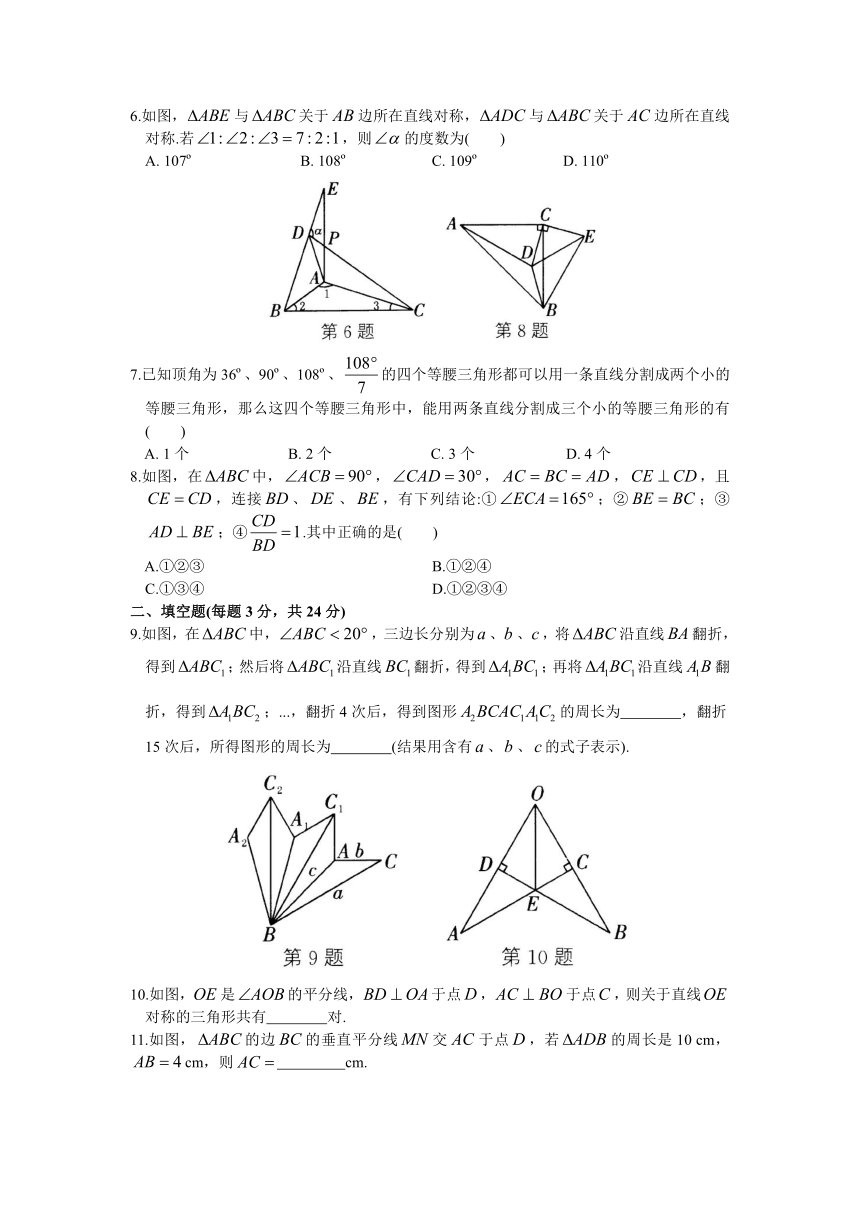
6.如图,与关于边所在直线对称,与关于边所在直线对称.若,则的度数为( )
A. 107o B. 108o C. 109o D. 110o
7.已知顶角为36o、90o、108o、的四个等腰三角形都可以用一条直线分割成两个小的等腰三角形,那么这四个等腰三角形中,能用两条直线分割成三个小的等腰三角形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.如图,在中,,,,,且,连接、、,有下列结论:①;②;③;④.其中正确的是( )
A.①②③ B.①②④
C.①③④ D.①②③④
二、填空题(每题3分,共24分)
9.如图,在中,,三边长分别为、、,将沿直线翻折,得到;然后将沿直线翻折,得到;再将沿直线翻折,得到;...,翻折4次后,得到图形的周长为 ,翻折15次后,所得图形的周长为 (结果用含有、、的式子表示).
10.如图,是的平分线,于点,于点,则关于直线 对称的三角形共有 对.
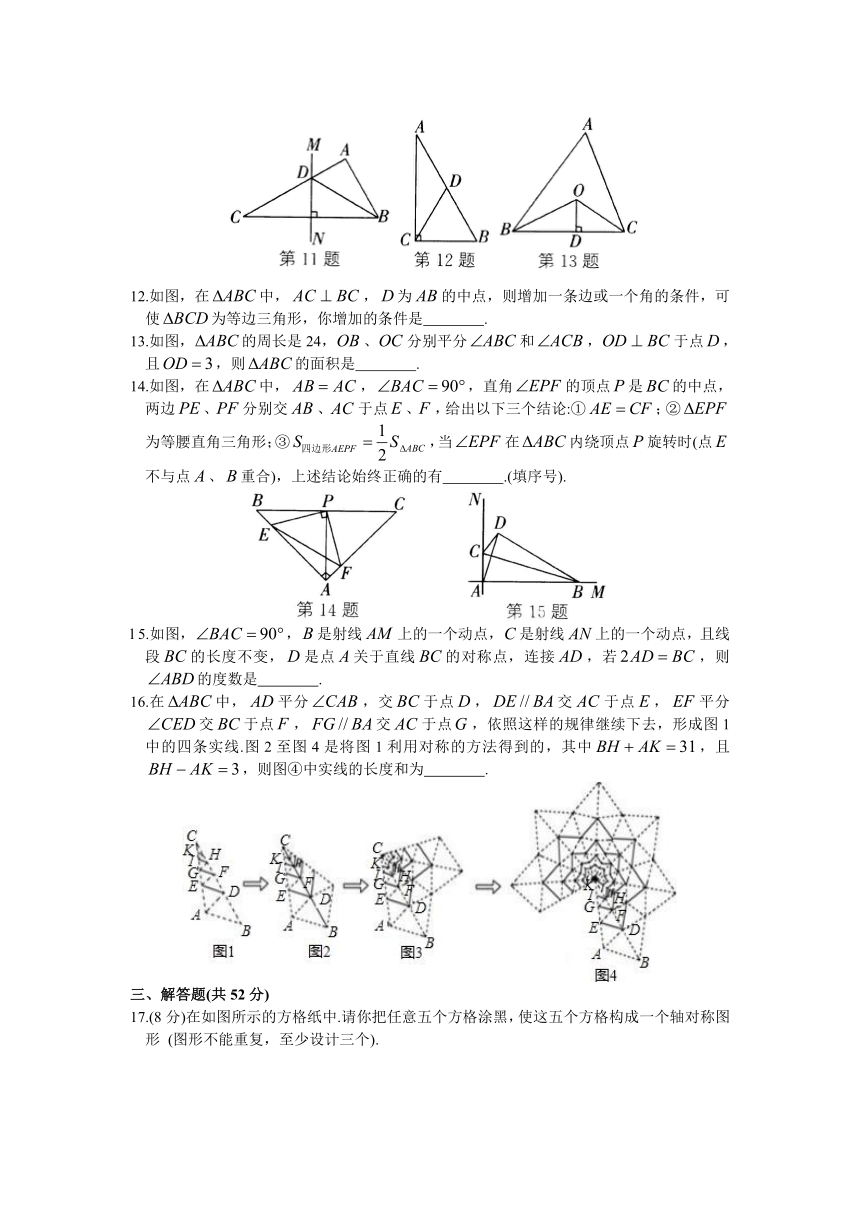
11.如图,的边的垂直平分线交于点,若的周长是10 cm,cm,则 cm.
12.如图,在中,,为的中点,则增加一条边或一个角的条件,可使为等边三角形,你增加的条件是 .
13.如图,的周长是24,、分别平分和,于点,且,则的面积是 .
14.如图,在中,,,直角的顶点是的中点,两边、分别交、于点、,给出以下三个结论:①;②为等腰直角三角形;③,当在内绕顶点旋转时(点不与点、重合),上述结论始终正确的有 .(填序号).
l 5.如图,,是射线上的一个动点,是射线上的一个动点,且线段的长度不变,是点关于直线的对称点,连接,若,则的度数是 .
16.在中,平分,交于点,交于点,平分交于点,交于点,依照这样的规律继续下去,形成图1中的四条实线.图2至图4是将图1利用对称的方法得到的,其中,且,则图④中实线的长度和为 .
三、解答题(共52分)
17.(8分)在如图所示的方格纸中.请你把任意五个方格涂黑,使这五个方格构成一个轴对称图形 (图形不能重复,至少设计三个).
18. (8分)如图①,在等腰三角形中,,,为外部的一点.在的右侧作,且.
(1)探究线段、和的数量关系.
(2)如图②,若将“”改为“”.(1)中的结论是否还成立?若成立.给出证明;若不成立,给出正确的结论.并简要说明理由.
19. (8分)如图,在中,,的垂直平分线交于点,垂足为,连接,若,.求:
(1) 的度数;
(2)的长度.
20. (8分)如图,在中,,是边上一点,于点,,交于点,是的中点,连接.求证: .
21. (8分)如图,在中,,、分别平分、,交 于点,连接.
(1)直接写出与之间的关系式;
(2)求证: 为等腰三角形;
(3)当的大小满足什么条件时,以、、为顶点的三角形为等腰三角形?
22. (12分)在中,,是中垂线上一动点,连接,直线 交于点,是点关于的对称点,连接并延长,交于点,连接交于点.
(1)如图②,当点移动到上时,点、、重合,若,则
(用含、的式子表示);
(2)当点移动到的上方时,如图③,其他条件不变,求证: ;
(3)当点移动到的内部时,其他条件不变,线段、、有什么确定的数量关系,请画出图形,并直接写出结论(不必证明).
参考答案
1-8 CCBDCBDD
9.
10. 4
11. 6
12. 答案不唯一,如
13. 36
14. ①②③
15. 30o或150o
16. 168
17.答案不唯一,如图所示
18.(1)
(2)不成立,
19. (1)
(2)
20.提示:
21. (1)
(2) 提示:
(3) 当为72o或时,以、、为顶点的三角形为等腰三角形.
22. (1)
(2) 提示:
(3) .
(满分:100分 时间:90分钟)
一、选择题(每题3分,共24分)
1.观察下列各组图形,其中不是轴对称的是( )
2.把一张长方形纸片按如图①、②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
3.如图,在由相同的小正方形组成的的网格中,有3个小正方形已经涂黑,请你再涂黑一个小正方形,使涂黑的四个小正方形构成的图形为轴对称图形,则还需要涂黑的小正方形的序号是( )
A.①或② B.③或⑥或⑦
C.④或⑤ D.③或⑨
4.如图,平分,且.若点、分别在、上,且为等边三角形,则满足上述条件的有( )
A. 2个 B. 3个 C. 4个 D.无数个
5.如图,、分别是、平分线上的点,于点,于点,于点,则下列结论错误的是( )
A.
B.
C. 与互佘的角有2个
D. 是的中点
6.如图,与关于边所在直线对称,与关于边所在直线对称.若,则的度数为( )
A. 107o B. 108o C. 109o D. 110o
7.已知顶角为36o、90o、108o、的四个等腰三角形都可以用一条直线分割成两个小的等腰三角形,那么这四个等腰三角形中,能用两条直线分割成三个小的等腰三角形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.如图,在中,,,,,且,连接、、,有下列结论:①;②;③;④.其中正确的是( )
A.①②③ B.①②④
C.①③④ D.①②③④
二、填空题(每题3分,共24分)
9.如图,在中,,三边长分别为、、,将沿直线翻折,得到;然后将沿直线翻折,得到;再将沿直线翻折,得到;...,翻折4次后,得到图形的周长为 ,翻折15次后,所得图形的周长为 (结果用含有、、的式子表示).
10.如图,是的平分线,于点,于点,则关于直线 对称的三角形共有 对.
11.如图,的边的垂直平分线交于点,若的周长是10 cm,cm,则 cm.
12.如图,在中,,为的中点,则增加一条边或一个角的条件,可使为等边三角形,你增加的条件是 .
13.如图,的周长是24,、分别平分和,于点,且,则的面积是 .
14.如图,在中,,,直角的顶点是的中点,两边、分别交、于点、,给出以下三个结论:①;②为等腰直角三角形;③,当在内绕顶点旋转时(点不与点、重合),上述结论始终正确的有 .(填序号).
l 5.如图,,是射线上的一个动点,是射线上的一个动点,且线段的长度不变,是点关于直线的对称点,连接,若,则的度数是 .
16.在中,平分,交于点,交于点,平分交于点,交于点,依照这样的规律继续下去,形成图1中的四条实线.图2至图4是将图1利用对称的方法得到的,其中,且,则图④中实线的长度和为 .
三、解答题(共52分)
17.(8分)在如图所示的方格纸中.请你把任意五个方格涂黑,使这五个方格构成一个轴对称图形 (图形不能重复,至少设计三个).
18. (8分)如图①,在等腰三角形中,,,为外部的一点.在的右侧作,且.
(1)探究线段、和的数量关系.
(2)如图②,若将“”改为“”.(1)中的结论是否还成立?若成立.给出证明;若不成立,给出正确的结论.并简要说明理由.
19. (8分)如图,在中,,的垂直平分线交于点,垂足为,连接,若,.求:
(1) 的度数;
(2)的长度.
20. (8分)如图,在中,,是边上一点,于点,,交于点,是的中点,连接.求证: .
21. (8分)如图,在中,,、分别平分、,交 于点,连接.
(1)直接写出与之间的关系式;
(2)求证: 为等腰三角形;
(3)当的大小满足什么条件时,以、、为顶点的三角形为等腰三角形?
22. (12分)在中,,是中垂线上一动点,连接,直线 交于点,是点关于的对称点,连接并延长,交于点,连接交于点.
(1)如图②,当点移动到上时,点、、重合,若,则
(用含、的式子表示);
(2)当点移动到的上方时,如图③,其他条件不变,求证: ;
(3)当点移动到的内部时,其他条件不变,线段、、有什么确定的数量关系,请画出图形,并直接写出结论(不必证明).
参考答案
1-8 CCBDCBDD
9.
10. 4
11. 6
12. 答案不唯一,如
13. 36
14. ①②③
15. 30o或150o
16. 168
17.答案不唯一,如图所示
18.(1)
(2)不成立,
19. (1)
(2)
20.提示:
21. (1)
(2) 提示:
(3) 当为72o或时,以、、为顶点的三角形为等腰三角形.
22. (1)
(2) 提示:
(3) .
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
