第6课时 解方程—方程的解 课件 (共25张PPT)
文档属性
| 名称 | 第6课时 解方程—方程的解 课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-14 00:00:00 | ||
图片预览




文档简介
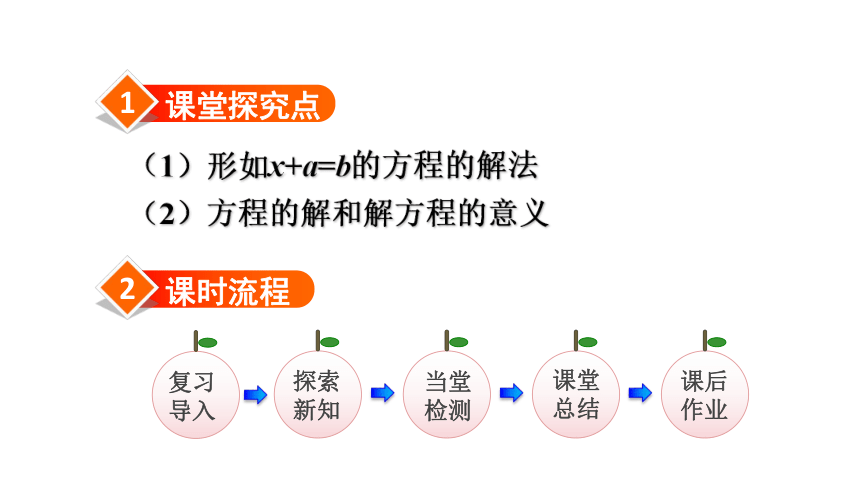
课件25张PPT。第 6 课时 解方程—方程的解 5 简易方程RJ 五年级上册 (1)形如x+a=b的方程的解法
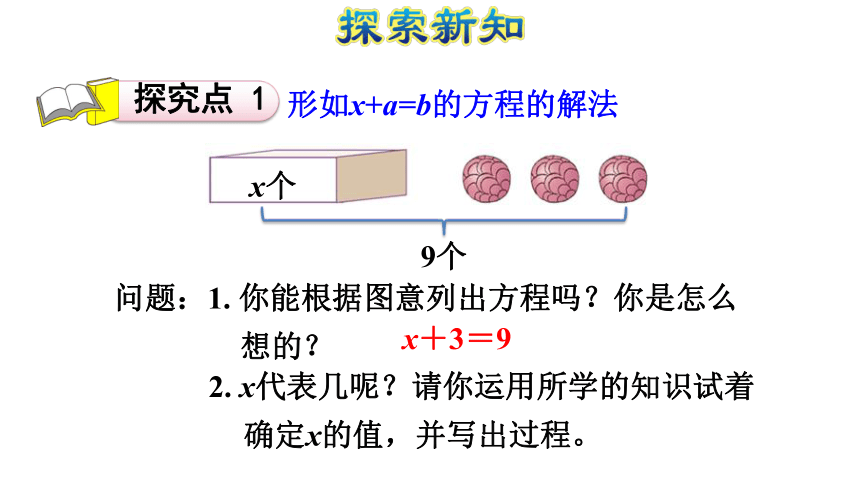
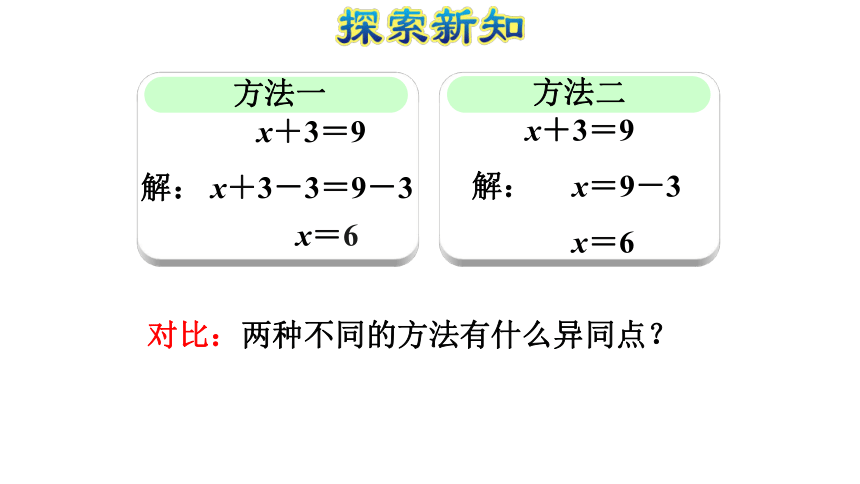
(2)方程的解和解方程的意义课后作业探索新知课堂总结当堂检测复习导入1.4x=9.8 ( )3x-8y=14 ( )16+y<30 ( ) 下面哪个式子是方程?21÷7=3 ( )形如x+a=b的方程的解法问题:1. 你能根据图意列出方程吗?你是怎么想的?x+3=9 2. x代表几呢?请你运用所学的知识试着确定x的值,并写出过程。x个9个方法一 x+3=9
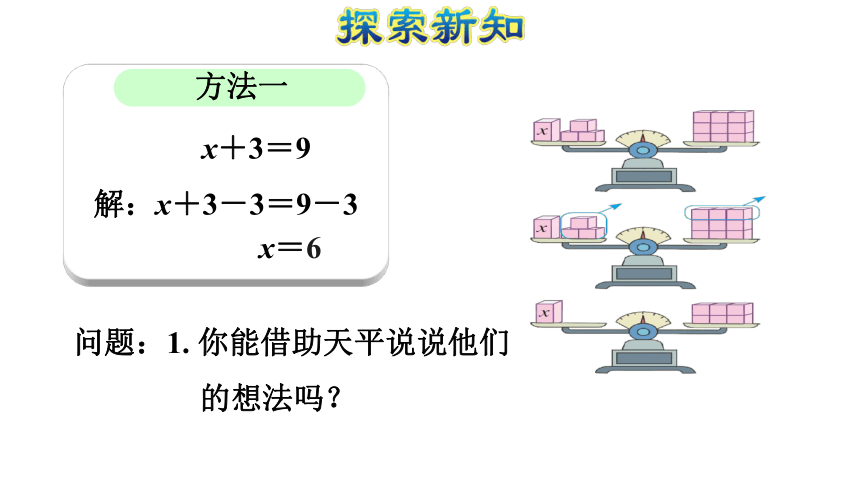
解:x+3-3=9-3
x=6 问题:1. 你能借助天平说说他们的想法吗?2. 第一种方法用到学过的什么知识?为什么要把等式的两边同时减3?为什么不同时减1? x+3=9
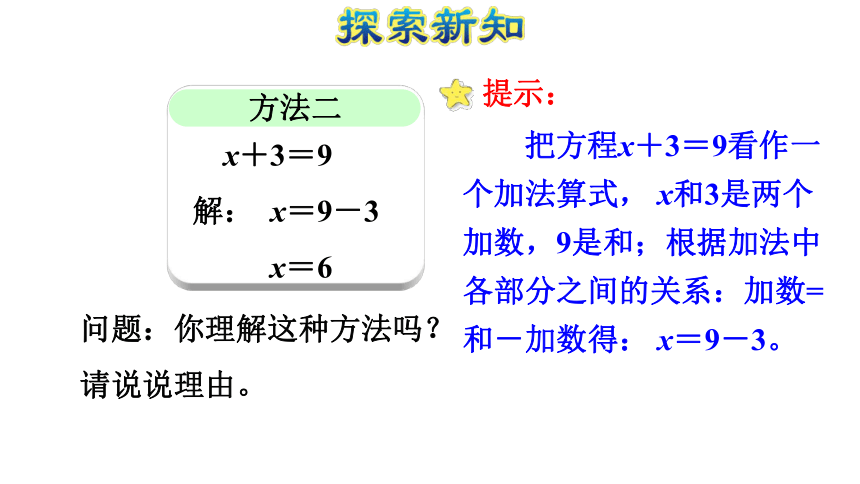
解: x=9-3
x=6问题:你理解这种方法吗?请说说理由。 把方程x+3=9看作一个加法算式, x和3是两个加数,9是和;根据加法中各部分之间的关系:加数=和-加数得: x=9-3。提示:方法二方法一 x+3=9
解: x+3-3=9-3
x=6方法二 x+3=9
解: x=9-3
x=6对比:两种不同的方法有什么异同点?提示: 在小学阶段,特别是刚刚学习解方程时,我们通常选用方法一解方程,方法二也可以看作是方法一的简写形式。归纳总结:形如x+a=b的方程的解法:
1.先写“解:”;
2. 在方程的两边同时减去a,使等式成立;
3.求出x的值。1. 解方程。 (选题源于教材P67第1题(3)) x-63=36解:x-63+63=36+63 x=992. 小诊所。 x-18=18 解: x=18-18 x=0 x=36改正:解: x=18+18方程的解和解方程的意义 x+3=9 解: x+3-3=9-3 x=6求方程的解的过程叫做解方程。使方程左右两边相等的未知数的值,叫做方程的解。思考:1.结合上例,说一说什么是解方程?什么是方程的解?
2.方程的解和解方程有什么区别?方程的解是一个数值,而解方程是一个过程。怎样检验一下答案是否正确呢? x+3=9 解: x+3-3=9-3 x=6归纳总结:1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.方程的解是一个数值,而解方程是一个过程。1. x=2是方程5x=15的解吗?x=3呢?
(选题源于教材P67做一做第2题)(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程.( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )2.判断。1.填一填。
x+0.5=2.5
解:x+0.5-( )= 2.5-( )
x= ( )
(1)使方程左右两边相等的未知数的值,叫做方程的( ),在上面的方程中,x=( )是方程的解。
(2)求方程的解的过程叫做( )。
0.50.52 解2解方程2.后面( )中哪个x的值是方程的解?用横
线画出来。
(1)x+19=21 (x=2,x=40)
(2)15-x=7 (x=22,x=8)
(3)6x=9 (x=1.5,x=2)
(4)6÷x=3 (x=2,x=0.2)3.解下列方程并检验。
28+x=48 ?解:28+x-28=48-28
x=20
所以,x=20是方程的解。检验:方程左边=28+x
=28+20
=48
=方程右边解:x+1.2-1.2=2.5-1.2
x=1.3
所以,x=1.3是方程的解。3.解下列方程并检验。
x+1.2=2.5
?检验:方程左边=x+1.2
=1.3+1.2
=2.5
=方程右边1.形如x+a=b的方程的解法:运用等式的性质1,在方程的左右两边同时减去a,可得到方程的解。
2.方程的解:使方程左右两边相等的未知数的值,叫做方程的解。
3.解方程:求方程的解的过程叫做解方程。
4.方程的解是一个数值,而解方程是一个过程。
课件PPT谢谢请领导老师批评指正
1.先写“解:”;
2. 在方程的两边同时减去a,使等式成立;
3.求出x的值。1. 解方程。 (选题源于教材P67第1题(3)) x-63=36解:x-63+63=36+63 x=992. 小诊所。 x-18=18 解: x=18-18 x=0 x=36改正:解: x=18+18方程的解和解方程的意义 x+3=9 解: x+3-3=9-3 x=6求方程的解的过程叫做解方程。使方程左右两边相等的未知数的值,叫做方程的解。思考:1.结合上例,说一说什么是解方程?什么是方程的解?
2.方程的解和解方程有什么区别?方程的解是一个数值,而解方程是一个过程。怎样检验一下答案是否正确呢? x+3=9 解: x+3-3=9-3 x=6归纳总结:1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.方程的解是一个数值,而解方程是一个过程。1. x=2是方程5x=15的解吗?x=3呢?
(选题源于教材P67做一做第2题)(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程.( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )2.判断。1.填一填。
x+0.5=2.5
解:x+0.5-( )= 2.5-( )
x= ( )
(1)使方程左右两边相等的未知数的值,叫做方程的( ),在上面的方程中,x=( )是方程的解。
(2)求方程的解的过程叫做( )。
0.50.52 解2解方程2.后面( )中哪个x的值是方程的解?用横
线画出来。
(1)x+19=21 (x=2,x=40)
(2)15-x=7 (x=22,x=8)
(3)6x=9 (x=1.5,x=2)
(4)6÷x=3 (x=2,x=0.2)3.解下列方程并检验。
28+x=48 ?解:28+x-28=48-28
x=20
所以,x=20是方程的解。检验:方程左边=28+x
=28+20
=48
=方程右边解:x+1.2-1.2=2.5-1.2
x=1.3
所以,x=1.3是方程的解。3.解下列方程并检验。
x+1.2=2.5
?检验:方程左边=x+1.2
=1.3+1.2
=2.5
=方程右边1.形如x+a=b的方程的解法:运用等式的性质1,在方程的左右两边同时减去a,可得到方程的解。
2.方程的解:使方程左右两边相等的未知数的值,叫做方程的解。
3.解方程:求方程的解的过程叫做解方程。
4.方程的解是一个数值,而解方程是一个过程。
课件PPT谢谢请领导老师批评指正
