1.1.1空间几何体的结构特征 课件
文档属性
| 名称 | 1.1.1空间几何体的结构特征 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-16 00:00:00 | ||
图片预览





文档简介
问题提出
1.在平面几何中,我们认识了三角形,正方形,矩形,菱形,梯形,圆,扇形等平面图形.那么对空间中各种各样的几何体,我们如何认识它们的结构特征?
2.对空间中不同形状、大小的几何体我们如何理解它们的联系和区别?
1.1
空间几何体的结构特征
知识探究(一):空间几何体的类型
思考1:在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.你能列举那些空间几何体的实例?
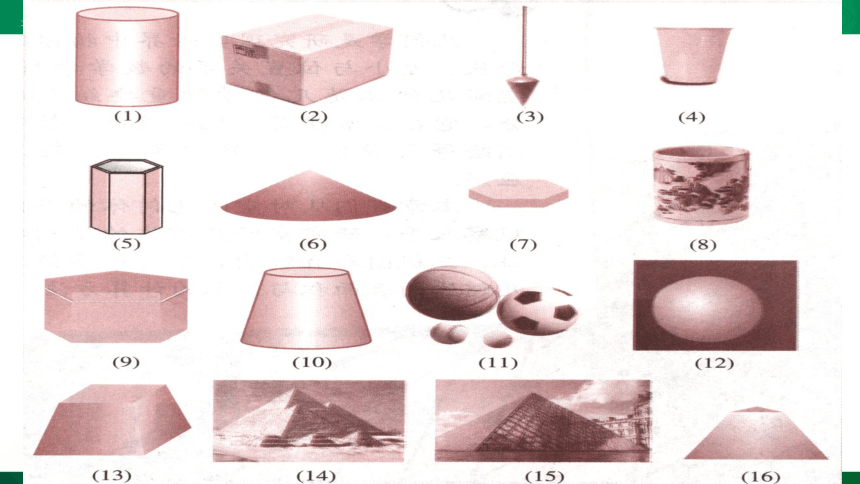
思考2:观察下列图片,你知道这图片在几何中分别叫什么名称吗?
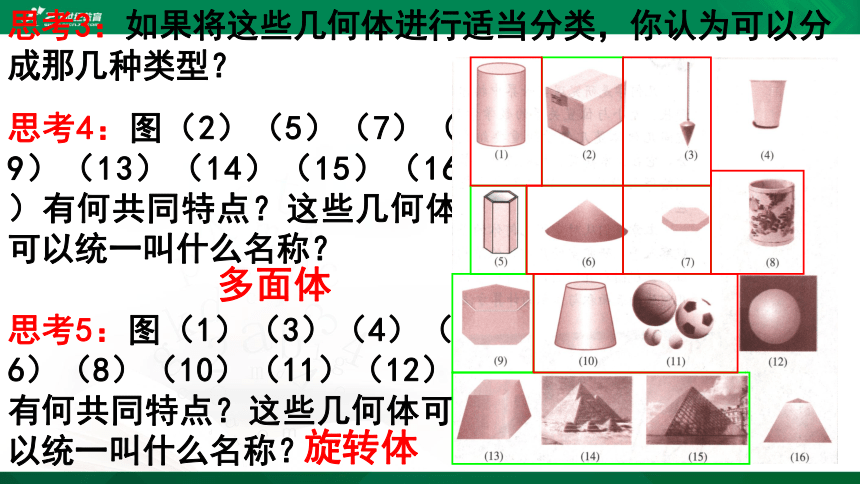
思考3:如果将这些几何体进行适当分类,你认为可以分成那几种类型?
思考4:图(2)(5)(7)(9)(13)(14)(15)(16)有何共同特点?这些几何体可以统一叫什么名称?
思考5:图(1)(3)(4)(6)(8)(10)(11)(12)有何共同特点?这些几何体可以统一叫什么名称?
多面体
旋转体
1.1.1
柱、锥、台、球的结构特征
1、多面体
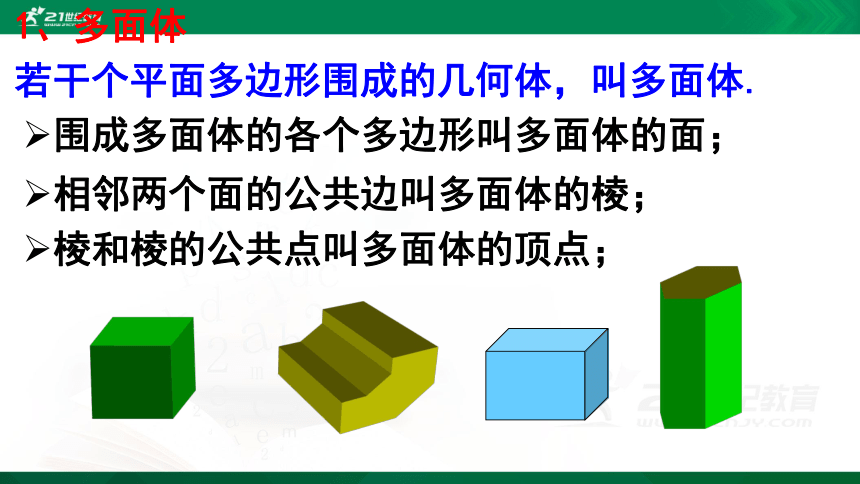
若干个平面多边形围成的几何体,叫多面体.
围成多面体的各个多边形叫多面体的面;
相邻两个面的公共边叫多面体的棱;
棱和棱的公共点叫多面体的顶点;
两个互相平行的面叫做棱柱的底面;
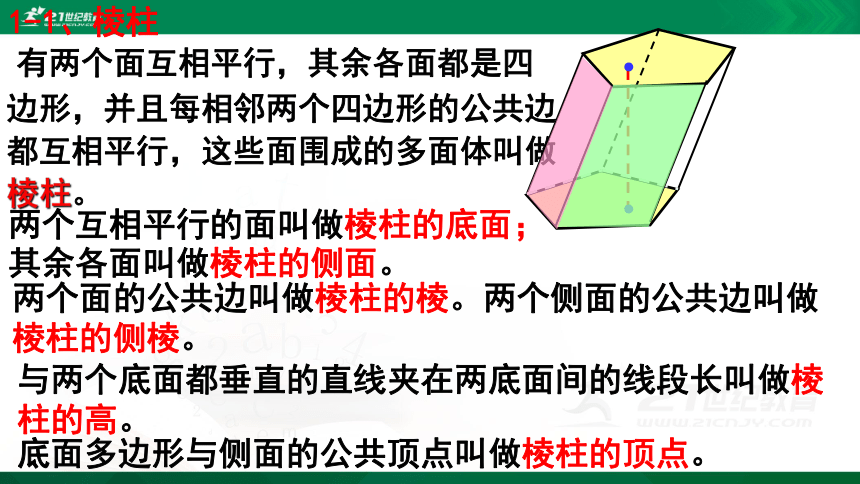
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱。
其余各面叫做棱柱的侧面。
1-1、棱柱
两个面的公共边叫做棱柱的棱。两个侧面的公共边叫做棱柱的侧棱。
与两个底面都垂直的直线夹在两底面间的线段长叫做棱柱的高。
底面多边形与侧面的公共顶点叫做棱柱的顶点。
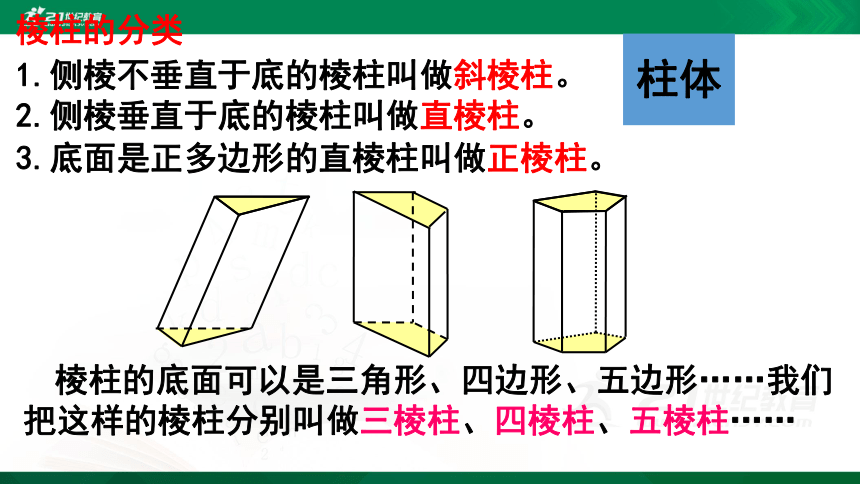
棱柱的分类
棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……
1.侧棱不垂直于底的棱柱叫做斜棱柱。
2.侧棱垂直于底的棱柱叫做直棱柱。
3.底面是正多边形的直棱柱叫做正棱柱。
柱体
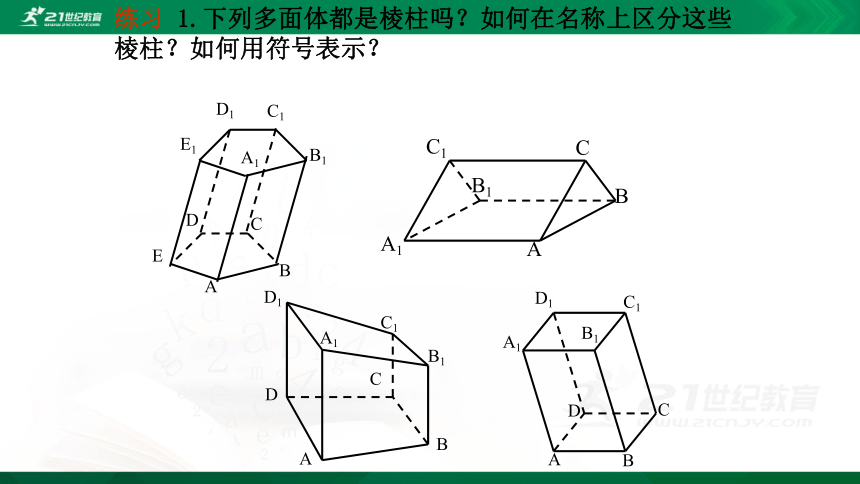
练习 1.下列多面体都是棱柱吗?如何在名称上区分这些棱柱?如何用符号表示?
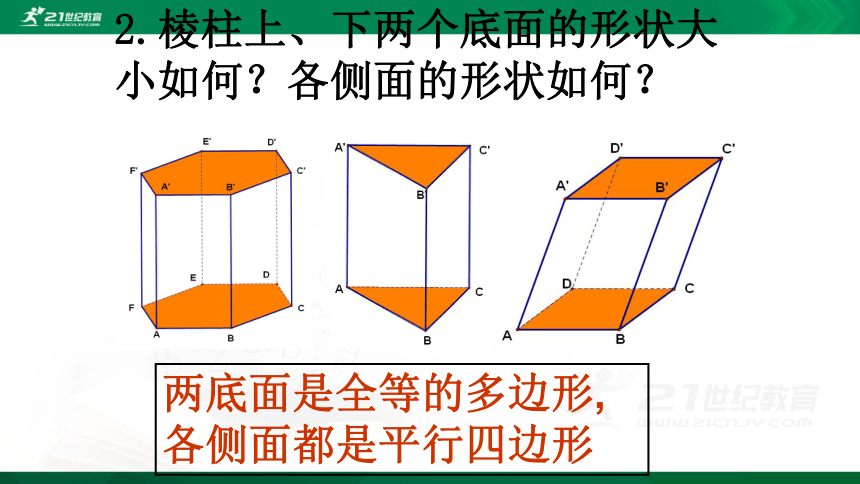
2.棱柱上、下两个底面的形状大小如何?各侧面的形状如何?
两底面是全等的多边形,各侧面都是平行四边形
3.有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?
4.一个棱柱至少有几个侧面?一个N棱柱分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
O
1-2、棱锥
(1) 一个面是多边形
(2) 其余各面都是有一个公共顶点的三角形
棱锥的分类
三棱锥
四棱锥
五棱锥
(四面体)
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.
正棱锥的基本性质
各侧棱相等,各侧面是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。
练习 1.下列多面体都是棱锥吗?如何在名称上区分这些棱锥?如何用符号表示?
2.一个棱锥至少有几个面?一个N棱锥有分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
至少有4个面;1个底面,N个侧面,N条侧棱,1个顶点.
1-3、棱台的概念
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台。
下底面
上底面
侧面
侧棱
高
顶点
斜高
用正棱锥截得的棱台叫作正棱台。
正棱台
正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。
正棱锥
正四棱台
棱柱、棱锥、棱台分别具有什么几何性质?有什么共同的性质?
棱
柱 两底面是对应边平行的全等多边形;
侧面、对角面都是平行四边形;侧棱平行且相等;
平行于底面的截面是与底面全等的多边形.
棱
锥 侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的
比的平方.
棱
台 两底面所在平面互相平行; 两底面是对应边互相平行的相似多边形;侧面是梯形;侧棱的延长线相交于一点.
理论迁移
例1 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱?
例2 一个三棱柱可以分割成几个三棱锥?
三棱柱
的切割
1.下图中不可能围成正方体的是( )
B
2.在棱柱中………………..( )
A . 只有两个面平行
B . 所有的棱都相等
C . 所有的面都是平行四边形
D . 两底面平行,并且各侧棱也平行
D
一个平面图形绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面。
封闭的旋转面围成的几何体叫作旋转体。
2、旋转体
2-1.圆柱、圆锥、圆台。
底面
侧面
母线
2-2. 球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫作球体,简称球。
球心
半径
直径
O
想一想:用一个平面去截一个球,截面是什么?
O
用一个截面去截一个球,截面是圆面。
球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的截面截得的圆叫球的小圆。
球、圆柱、圆锥、圆台过轴的截面分别是什么图形?
练习:
1、下列命题是正确的是( )
A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作( )个。
1或无数多
提高:长方体AC1中,AB=3,BC=2,BB1=1,由A到C1在长方体表面上的最短距离是多少?
简单几何体
简单旋转体
简单多面体
球
圆
柱
圆
锥
圆
台
棱
柱
棱
锥
棱
台
1.1.2
简单组合体的结构特征
日常生活中我们常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
简单组合体
由柱、锥、台、球组成了一些简单的组合体.认识它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
走在街上会看到一些物体,它们的主要几何结构特征是什么?
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特征呢?
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何结构特征是什么?
简单组合体
居民的住宅又有什么主要几何结构特征?
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成的吗?
简单组合体
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的呢?这个轮胎呢?
旋转体
数学在生活中无处不在,培养在生活中不断的用数学的眼光看问题,会逐渐激发学数学的兴趣,增强数学地分析问题、解决问题的能力.
生活与数学
作业:
P8习题1.1A组:
1题(1)(2)(3)(4);
5题(自主制作).
1.在平面几何中,我们认识了三角形,正方形,矩形,菱形,梯形,圆,扇形等平面图形.那么对空间中各种各样的几何体,我们如何认识它们的结构特征?
2.对空间中不同形状、大小的几何体我们如何理解它们的联系和区别?
1.1
空间几何体的结构特征
知识探究(一):空间几何体的类型
思考1:在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.你能列举那些空间几何体的实例?
思考2:观察下列图片,你知道这图片在几何中分别叫什么名称吗?
思考3:如果将这些几何体进行适当分类,你认为可以分成那几种类型?
思考4:图(2)(5)(7)(9)(13)(14)(15)(16)有何共同特点?这些几何体可以统一叫什么名称?
思考5:图(1)(3)(4)(6)(8)(10)(11)(12)有何共同特点?这些几何体可以统一叫什么名称?
多面体
旋转体
1.1.1
柱、锥、台、球的结构特征
1、多面体
若干个平面多边形围成的几何体,叫多面体.
围成多面体的各个多边形叫多面体的面;
相邻两个面的公共边叫多面体的棱;
棱和棱的公共点叫多面体的顶点;
两个互相平行的面叫做棱柱的底面;
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱。
其余各面叫做棱柱的侧面。
1-1、棱柱
两个面的公共边叫做棱柱的棱。两个侧面的公共边叫做棱柱的侧棱。
与两个底面都垂直的直线夹在两底面间的线段长叫做棱柱的高。
底面多边形与侧面的公共顶点叫做棱柱的顶点。
棱柱的分类
棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……
1.侧棱不垂直于底的棱柱叫做斜棱柱。
2.侧棱垂直于底的棱柱叫做直棱柱。
3.底面是正多边形的直棱柱叫做正棱柱。
柱体
练习 1.下列多面体都是棱柱吗?如何在名称上区分这些棱柱?如何用符号表示?
2.棱柱上、下两个底面的形状大小如何?各侧面的形状如何?
两底面是全等的多边形,各侧面都是平行四边形
3.有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?
4.一个棱柱至少有几个侧面?一个N棱柱分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
O
1-2、棱锥
(1) 一个面是多边形
(2) 其余各面都是有一个公共顶点的三角形
棱锥的分类
三棱锥
四棱锥
五棱锥
(四面体)
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.
正棱锥的基本性质
各侧棱相等,各侧面是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。
练习 1.下列多面体都是棱锥吗?如何在名称上区分这些棱锥?如何用符号表示?
2.一个棱锥至少有几个面?一个N棱锥有分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
至少有4个面;1个底面,N个侧面,N条侧棱,1个顶点.
1-3、棱台的概念
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台。
下底面
上底面
侧面
侧棱
高
顶点
斜高
用正棱锥截得的棱台叫作正棱台。
正棱台
正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。
正棱锥
正四棱台
棱柱、棱锥、棱台分别具有什么几何性质?有什么共同的性质?
棱
柱 两底面是对应边平行的全等多边形;
侧面、对角面都是平行四边形;侧棱平行且相等;
平行于底面的截面是与底面全等的多边形.
棱
锥 侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的
比的平方.
棱
台 两底面所在平面互相平行; 两底面是对应边互相平行的相似多边形;侧面是梯形;侧棱的延长线相交于一点.
理论迁移
例1 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱?
例2 一个三棱柱可以分割成几个三棱锥?
三棱柱
的切割
1.下图中不可能围成正方体的是( )
B
2.在棱柱中………………..( )
A . 只有两个面平行
B . 所有的棱都相等
C . 所有的面都是平行四边形
D . 两底面平行,并且各侧棱也平行
D
一个平面图形绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面。
封闭的旋转面围成的几何体叫作旋转体。
2、旋转体
2-1.圆柱、圆锥、圆台。
底面
侧面
母线
2-2. 球
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫作球体,简称球。
球心
半径
直径
O
想一想:用一个平面去截一个球,截面是什么?
O
用一个截面去截一个球,截面是圆面。
球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的截面截得的圆叫球的小圆。
球、圆柱、圆锥、圆台过轴的截面分别是什么图形?
练习:
1、下列命题是正确的是( )
A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。
A
2、过球面上的两点作球的大圆,可以作( )个。
1或无数多
提高:长方体AC1中,AB=3,BC=2,BB1=1,由A到C1在长方体表面上的最短距离是多少?
简单几何体
简单旋转体
简单多面体
球
圆
柱
圆
锥
圆
台
棱
柱
棱
锥
棱
台
1.1.2
简单组合体的结构特征
日常生活中我们常用到的日用品,比如:消毒液、暖瓶、洗洁精等的主要几何结构特征是什么?
简单组合体
由柱、锥、台、球组成了一些简单的组合体.认识它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
走在街上会看到一些物体,它们的主要几何结构特征是什么?
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特征呢?
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几何结构特征是什么?
简单组合体
居民的住宅又有什么主要几何结构特征?
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的主要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而成的吗?
简单组合体
你能想象这条曲线绕轴旋转而成的几何图形吗?
这顶可爱的草帽又是由什么样的曲线旋转而成的呢?这个轮胎呢?
旋转体
数学在生活中无处不在,培养在生活中不断的用数学的眼光看问题,会逐渐激发学数学的兴趣,增强数学地分析问题、解决问题的能力.
生活与数学
作业:
P8习题1.1A组:
1题(1)(2)(3)(4);
5题(自主制作).
