1.2.1-2中心投影与平行投影,空间几何体的三视图 课件
文档属性
| 名称 | 1.2.1-2中心投影与平行投影,空间几何体的三视图 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-16 00:00:00 | ||
图片预览





文档简介
1.2.2
空间几何体的三视图
【高考导航】三视图是高考的必考题型,以选择题形式出现,分值5分。
【学习目标】
1. 了解中心投影与平行投影的区别;
2. 能画出简单空间图形的三视图;
3. 能识别三视图所表示的空间几何体;
【学习重点】:三视图的画法及识别
【学习难点】:由立体图形画三视图,或由三视图识别其所表示的立体图形.
一.问题引入:
请同学们看下面几个常见的自然
现象,考虑它们是怎样得到的?
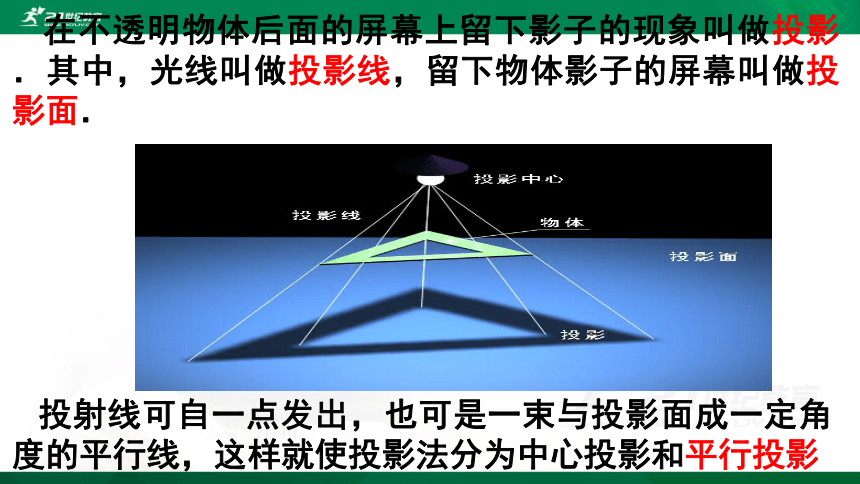
在不透明物体后面的屏幕上留下影子的现象叫做投影.其中,光线叫做投影线,留下物体影子的屏幕叫做投影面.
投射线可自一点发出,也可是一束与投影面成一定角度的平行线,这样就使投影法分为中心投影和平行投影
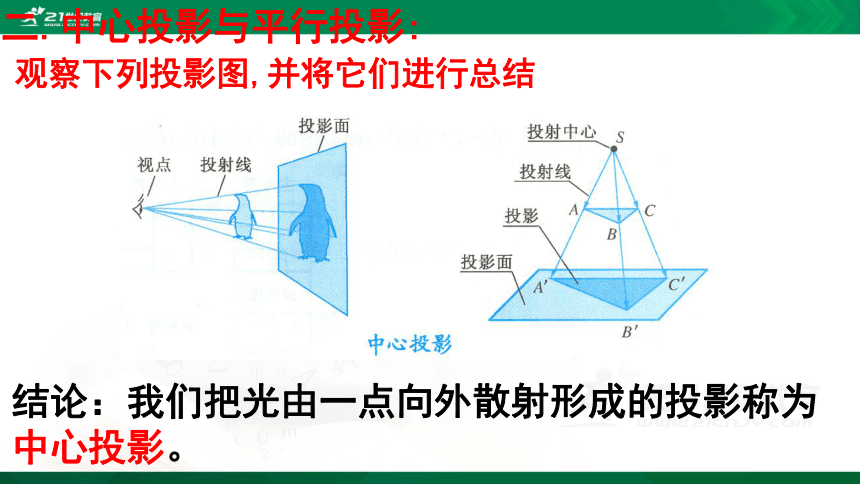
观察下列投影图,并将它们进行总结
结论:我们把光由一点向外散射形成的投影称为中心投影。
光由一点向外散射形成的投影,叫做中心投影.其投影线交于一点(投影中心).
在中心投影中,如果改变物体与投射中心或投影面之间的距离、位置,则其投影的大小也随之改变.
中心投影后的图形与原图形相比,虽然改变很多,但直观性强,看起来与人的视觉效果一致,最象原来的物体.所以在绘画时,经常使用这种方法,但在立体几何中很少用中心投影原理来画图.
从图中可以看出,空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线.
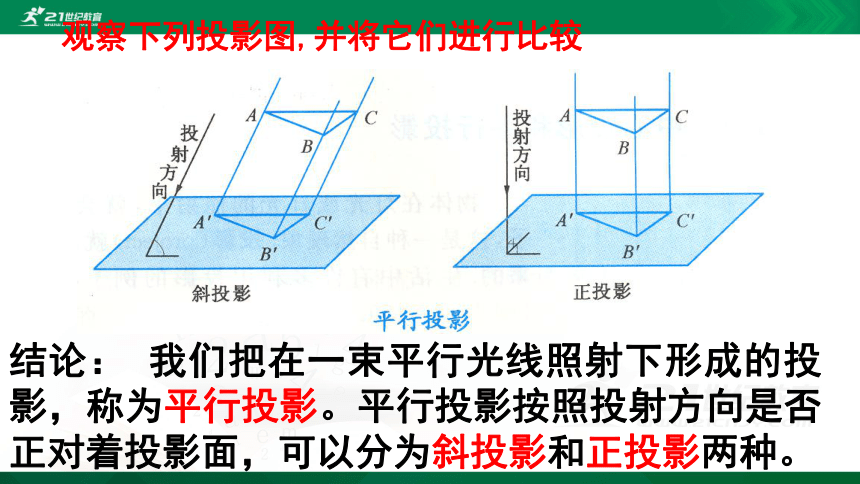
观察下列投影图,并将它们进行比较
结论: 我们把在一束平行光线照射下形成的投影,称为平行投影。平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种。
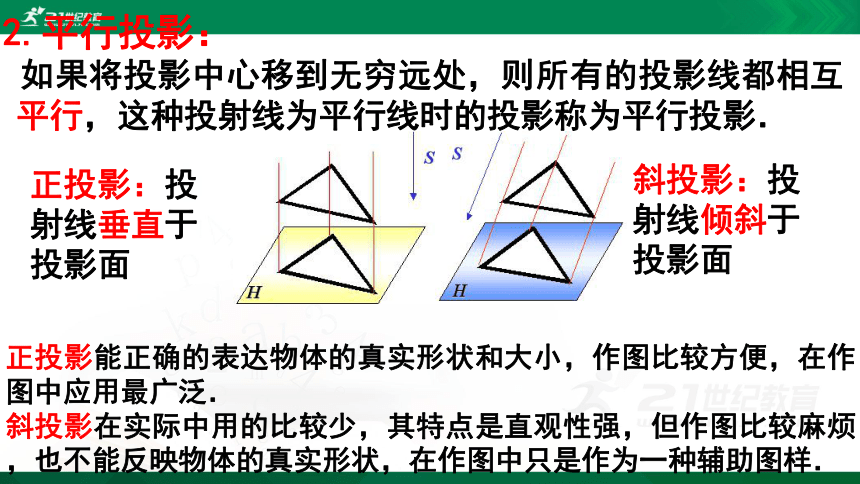
如果将投影中心移到无穷远处,则所有的投影线都相互平行,这种投射线为平行线时的投影称为平行投影.
斜投影:投射线倾斜于投影面
正投影:投射线垂直于投影面
正投影能正确的表达物体的真实形状和大小,作图比较方便,在作图中应用最广泛.
斜投影在实际中用的比较少,其特点是直观性强,但作图比较麻烦,也不能反映物体的真实形状,在作图中只是作为一种辅助图样.
S
投射方向
投射方向
三角板在中心投影和不同方向的平行投影下的投影效果
物体上某一点与其投影面上的投影点的连线是平行的,则为平行投影,如果聚于一点,则为中心投影.
投影的分类
中心投影:投射线交于一点
平行投影
斜投影
正投影
投射线平行
猜猜他们是什么关系?
看事物不能只看单方面
正 投 影
三视图的形成原理
视图:是指将物体按正投影向投影面投射所得到的图形.
三视图
正视图:光线自物体的前面向后面投射所得的投影称主视图或正视图;
俯视图:光线自物体的上面向下面投射所得的投影称俯视图;
侧视图:光线自物体的左面向右面投射所得的投影称左视图或侧视图;
正视图反映了物体的高度和长度
侧视图反映了物体的高度和宽度
俯视图反映了物体的长度和宽度
正视图
侧视图
俯视图
长对正
高平齐
宽相等
长对正
高平齐
宽相等
圆柱的三视图
四棱锥的三视图
圆锥的三视图
四棱台的三视图
圆台的三视图
球体的三视图
例1 画出下列物体的三视图:
例2 说出下列三视图表示的几何体:
(1)
主视图 左视图 俯视图
(2)
主视图 左视图 俯视图
3
(3)
课堂总结:
(1)涉及知识点:
中心投影与平行投影;
空间几何体的三视图;
三视图之间的投影规律:长对正、高平齐、宽相等。
(2)涉及数学思想方法:
转化与化归思想;数形结合思想。
空间几何体的三视图
【高考导航】三视图是高考的必考题型,以选择题形式出现,分值5分。
【学习目标】
1. 了解中心投影与平行投影的区别;
2. 能画出简单空间图形的三视图;
3. 能识别三视图所表示的空间几何体;
【学习重点】:三视图的画法及识别
【学习难点】:由立体图形画三视图,或由三视图识别其所表示的立体图形.
一.问题引入:
请同学们看下面几个常见的自然
现象,考虑它们是怎样得到的?
在不透明物体后面的屏幕上留下影子的现象叫做投影.其中,光线叫做投影线,留下物体影子的屏幕叫做投影面.
投射线可自一点发出,也可是一束与投影面成一定角度的平行线,这样就使投影法分为中心投影和平行投影
观察下列投影图,并将它们进行总结
结论:我们把光由一点向外散射形成的投影称为中心投影。
光由一点向外散射形成的投影,叫做中心投影.其投影线交于一点(投影中心).
在中心投影中,如果改变物体与投射中心或投影面之间的距离、位置,则其投影的大小也随之改变.
中心投影后的图形与原图形相比,虽然改变很多,但直观性强,看起来与人的视觉效果一致,最象原来的物体.所以在绘画时,经常使用这种方法,但在立体几何中很少用中心投影原理来画图.
从图中可以看出,空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线.
观察下列投影图,并将它们进行比较
结论: 我们把在一束平行光线照射下形成的投影,称为平行投影。平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种。
如果将投影中心移到无穷远处,则所有的投影线都相互平行,这种投射线为平行线时的投影称为平行投影.
斜投影:投射线倾斜于投影面
正投影:投射线垂直于投影面
正投影能正确的表达物体的真实形状和大小,作图比较方便,在作图中应用最广泛.
斜投影在实际中用的比较少,其特点是直观性强,但作图比较麻烦,也不能反映物体的真实形状,在作图中只是作为一种辅助图样.
S
投射方向
投射方向
三角板在中心投影和不同方向的平行投影下的投影效果
物体上某一点与其投影面上的投影点的连线是平行的,则为平行投影,如果聚于一点,则为中心投影.
投影的分类
中心投影:投射线交于一点
平行投影
斜投影
正投影
投射线平行
猜猜他们是什么关系?
看事物不能只看单方面
正 投 影
三视图的形成原理
视图:是指将物体按正投影向投影面投射所得到的图形.
三视图
正视图:光线自物体的前面向后面投射所得的投影称主视图或正视图;
俯视图:光线自物体的上面向下面投射所得的投影称俯视图;
侧视图:光线自物体的左面向右面投射所得的投影称左视图或侧视图;
正视图反映了物体的高度和长度
侧视图反映了物体的高度和宽度
俯视图反映了物体的长度和宽度
正视图
侧视图
俯视图
长对正
高平齐
宽相等
长对正
高平齐
宽相等
圆柱的三视图
四棱锥的三视图
圆锥的三视图
四棱台的三视图
圆台的三视图
球体的三视图
例1 画出下列物体的三视图:
例2 说出下列三视图表示的几何体:
(1)
主视图 左视图 俯视图
(2)
主视图 左视图 俯视图
3
(3)
课堂总结:
(1)涉及知识点:
中心投影与平行投影;
空间几何体的三视图;
三视图之间的投影规律:长对正、高平齐、宽相等。
(2)涉及数学思想方法:
转化与化归思想;数形结合思想。
