24.1.2 垂直于弦的直径课时作业

24.1.2 垂直于弦的直径课时作业
姓名：__________班级：__________考号：__________
、选择题
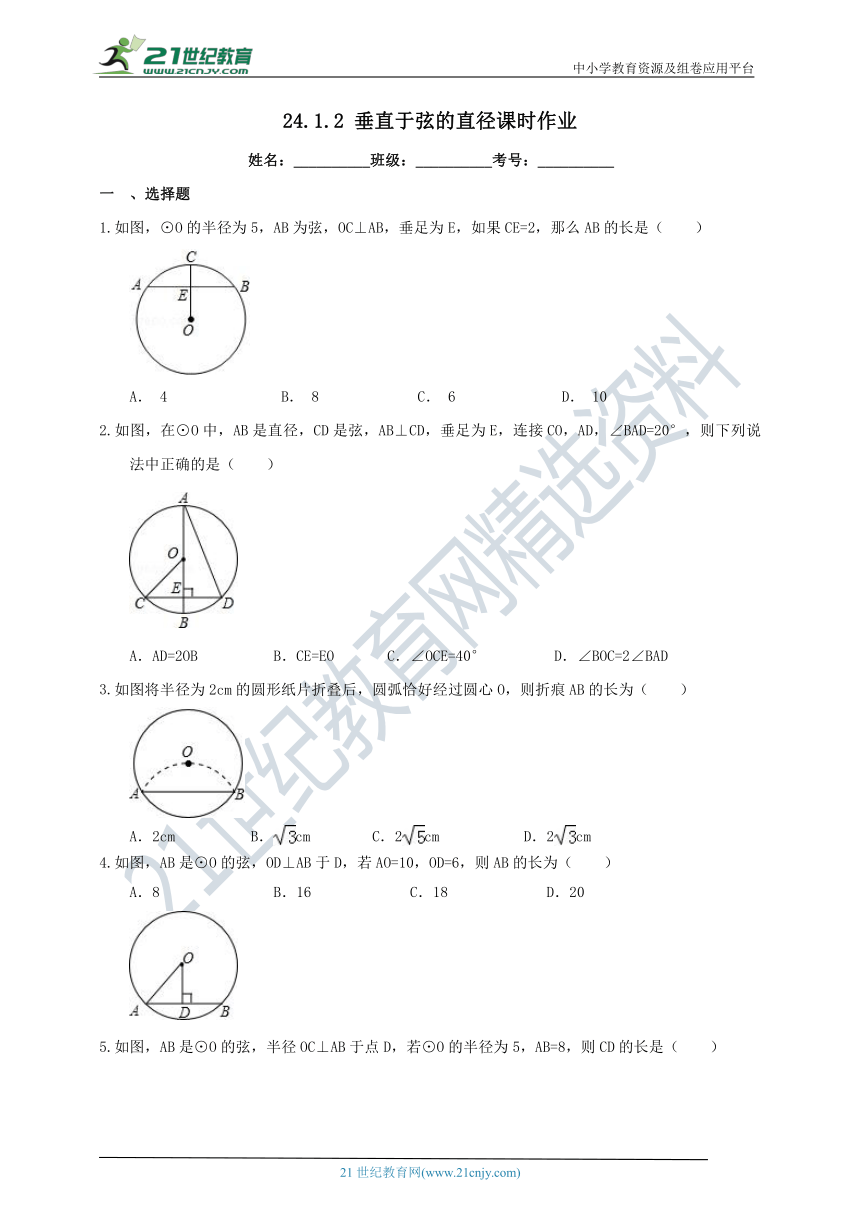
1.如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为E，如果CE=2，那么AB的长是（　　）
A． 4 B． 8 C． 6 D． 10
2.如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（　　）
A．AD=2OB B．CE=EO C．∠OCE=40° D．∠BOC=2∠BAD
3.如图将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为（　　）
A．2cm B．cm C．2cm D．2cm
4.如图，AB是⊙O的弦，OD⊥AB于D，若AO=10，OD=6，则AB的长为（　　）
A．8 B．16 C．18 D．20
5.如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（　　）
A．2 B．3 C．4 D．5
6.如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的直径为（　　）
A．5cm B．10cm C．6cm D．14cm
7.如图，⊙O的半径OA=6，以A为圆心，OA为半径的弧交⊙O于B、C点，则BC=（　　）
A． B． C． D．
8.⊙O过点B，C，圆心O在等腰直角△ABC内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（ ）
A． B． 2 C． D． 3
、填空题
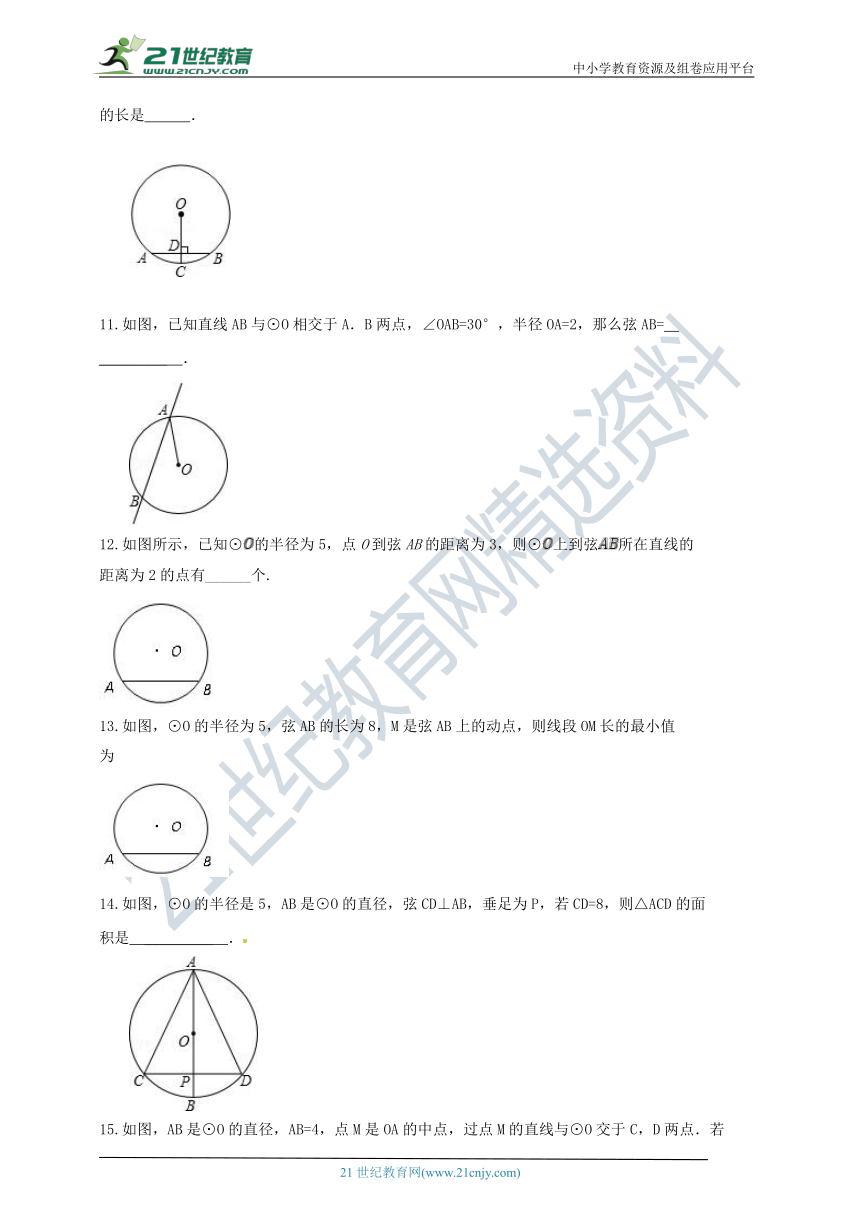
9.如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架
子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为　　cm．
10.如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD=1，则弦AB
的长是 ．
11.如图，已知直线AB与⊙O相交于A．B两点，∠OAB=30°，半径OA=2，那么弦AB=　
_________　．
12.如图所示，已知⊙的半径为5，点O到弦AB的距离为3，则⊙上到弦所在直线的
距离为2的点有______个.
13.如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值
为
14.如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面
积是　_________　．
15.如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C，D两点．若
∠CMA=45°，则弦CD的长为 ．
、解答题
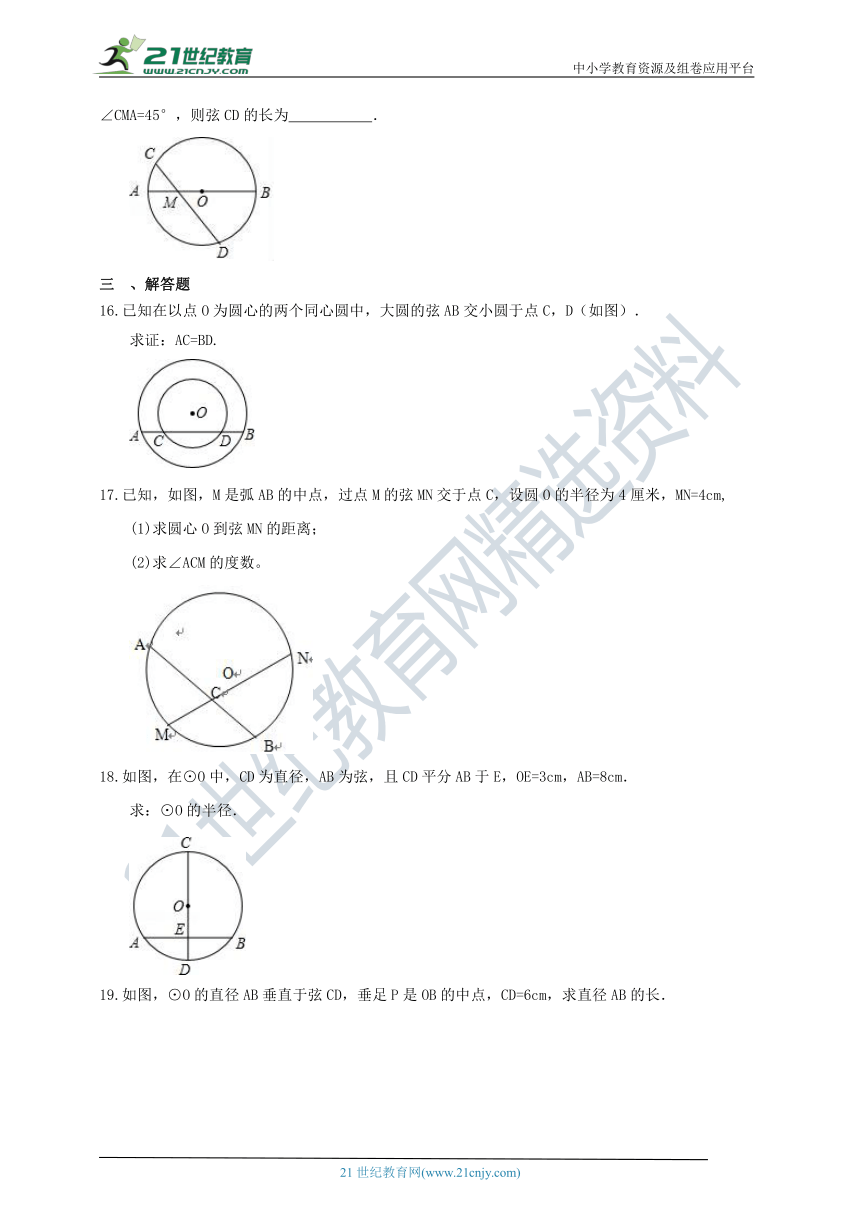
16.已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．
求证：AC=BD.
17.已知，如图，M是弧AB的中点，过点M的弦MN交于点C，设圆O的半径为4厘米，MN=4cm,
(1)求圆心O到弦MN的距离；
(2)求∠ACM的度数。
18.如图，在⊙O中，CD为直径，AB为弦，且CD平分AB于E，OE=3cm，AB=8cm．
求：⊙O的半径．
19.如图，⊙O的直径AB垂直于弦CD，垂足P是OB的中点，CD=6cm，求直径AB的长．
20.如图，⊙O的直径为10cm，弦AB=8cm，P是弦AB上的一个动点，求OP的长度范围．
21.如图，AB为于点D，过点D作的切线，交BA的延长线于点E.
(1) 求证：AC∥DE:
(2)连接CD，若OA＝AE＝a，写出求四边形ACDE面积的思路。
答案解析
、选择题
1.【考点】垂径定理；勾股定理．
【分析】连接OA，由于半径OC⊥AB，利用垂径定理可知AB=2AE，又CE=2，OC=5，易求OE，在Rt△AOE中利用勾股定理易求AE，进而可求AB．
解：连接OA，
∵半径OC⊥AB，
∴AE=BE=AB，
∵OC=5，CE=2，
∴OE=3，
在Rt△AOE中，AE===4，
∴AB=2AE=8，
故选B．
【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
2.【考点】垂径定理．
【分析】先根据垂径定理得到=，CE=DE，再利用圆周角定理得到∠BOC=40°，则根据互余可计算出∠OCE的度数，于是可对各选项进行判断．
解：∵AB⊥CD，
∴=，CE=DE，
∴∠BOC=2∠BAD=40°，
∴∠OCE=90°﹣40°=50°．
故选D．
3.【考点】垂径定理；翻折变换（折叠问题）．
【分析】通过作辅助线，过点O作OD⊥AB交AB于点D，根据折叠的性质可知OA=2OD，根据勾股定理可将AD的长求出，通过垂径定理可求出AB的长．
解：过点O作OD⊥AB交AB于点D，连接OA，
∵OA=2OD=2cm，
∴AD===（cm），
∵OD⊥AB，
∴AB=2AD=2cm．
故选：D．
4.【考点】垂径定理，勾股定理
【分析】先根据勾股定理求出AD的长，再根据垂径定理求出AB的长．
解：∵AB是⊙O的弦，OD⊥AB于D，
∴AD=BD=AB（垂径定理），
∴AB=2AD，
在Rt△ADO中，OD⊥AB于D，若AO=10，OD=6，
∴AD=8（勾股定理）；
∴AB=16．
故选B．
5.【考点】垂径定理；勾股定理．
【分析】根据垂径定理由OC⊥AB得到AD=AB=4，再根据勾股定理可求出OD，然后用OC﹣OD即可得到DC．
解：∵OC⊥AB，
∴AD=BD=AB=×8=4，
在Rt△OAD中，OA=5，AD=4，
∴OD==3，
∴CD=OC﹣OD=5﹣3=2．
故选A．
6.【考点】垂径定理，勾股定理
【分析】过O作直径CD⊥AB于E，连接OA，则OE=3cm，AE=BE= AB=4cm，在Rt△AEO中，由勾股定理求出OA，即可得出答案．
解：如图，
过O作直径CD⊥AB于E，连接OA，
则OE=3cm，AE=BE=AB=4cm，
在Rt△AEO中，由勾股定理得：OA= =5（cm），
则直径CD=2OA=10cm，
故选B．
7.【考点】勾股定理；垂径定理
【分析】根据垂径定理先求BC一半的长，再求BC的长．
解：设OA与BC相交于D点．
∵AB=OA=OB=6
∴△OAB是等边三角形．
又根据垂径定理可得，OA平分BC，
利用勾股定理可得BD==3
所以BC=6．
故选：A．
【点评】本题的关键是利用垂径定理和勾股定理．
8.【考点】垂径定理；勾股定理；等腰直角三角形．
【分析】根据等腰三角形三线合一的性质知：若过A作BC的垂线，设垂足为D，则AD必垂直平分BC；由垂径定理可知，AD必过圆心O；根据等腰直角三角形的性质，易求出BD、AD的长，进而可求出OD的值；连接OB根据勾股定理即可求出⊙O的半径．
解：过A作AD⊥BC，由题意可知AD必过点O，连接OB；[来源:学&科&网Z&X&X&K]
∵△BAC是等腰直角三角形，AD⊥BC，
∴BD=CD=AD=3；
∴OD=AD﹣OA=2；
Rt△OBD中，根据勾股定理，得：
OB==．
故选C．

【点评】本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
、填空题
9.【考点】垂径定理的应用．
【分析】设圆的圆心为O，连接OA，OC，OC与AB交于点D，设⊙O半径为R，在RT△AOD中利用勾股定理即可解决问题．
【解答】解；如图，设圆的圆心为O，连接OA，OC，OC与AB交于点D，设⊙O半径为R，
∵OC⊥AB，
∵AD=DB=AB=20，
在RT△AOD中，∵∠ADO=90°，
∴OA2=OD2+AD2，
∴R2=202+（R﹣10）2，
∴R=25．
故答案为25．
10.【考点】垂径定理；勾股定理．
【分析】连接AO，得到直角三角形，再求出OD的长，就可以利用勾股定理求解．
解：连接AO，
∵半径是5，CD=1，
∴OD=5﹣1=4，
根据勾股定理，
AD===3，
∴AB=3×2=6，
因此弦AB的长是6．

【点评】解答此题不仅要用到垂径定理，还要作出辅助线AO，这是解题的关键．
11.【考点】垂径定理；含30度角的直角三角形；勾股定理．
【分析】过O作OC⊥AB于C，根据垂直和垂径定理求出AB=2AC，∠OCA=90°，根据含
30度角的直角三角形性质求出OC=1，根据勾股定理求出AC，即可得出答案．
解：过O作OC⊥AB于C，
则AB=2AC，∠OCA=90°，
∵OA=2，∠OAB=30°，
∴OC=1，由勾股定理得：AC==，
∴AB=2AC=2，
故答案为：2．
【点评】本题考查了垂径定理，含30度角的直角三角形性质，勾股定理的应用，解此题的关键是正确作出辅助线后求出AC的长和得出AB=2AC，注意：垂直于弦的直径平分这条弦．
12. 【考点】垂径定理；勾股定理．
【分析】在弦AB的两侧分别有一个和两个点符合要求.
解：如图OD=OA=OB=5，OE⊥AB，OE=3，∴DE=OD-OE=5-3=2cm，∴点D是圆上到AB距离为2cm的点，∵OE=3cm＞2cm，∴在OD上截取OH=1cm，过点H作GF∥AB，交圆于点G，F两点，则有HE⊥AB，HE=OE-OH=2cm，即GF到AB的距离为2cm，∴点G，F也是圆上到AB距离为2cm的点．故答案为3．
13.【考点】垂径定理，勾股定理
【分析】过O作OM⊥AB于M，此时线段OM的长最短，连接OA，根据垂径定理求出AM，根据勾股定理求出OM即可．
解：如图：
过O作OM⊥AB于M，此时线段OM的长最短，连接OA，
∵OM过O，OM⊥AB，
∴AM=AB=×8=4，
在Rt△AMO中，由勾股定理得：OM= =3，
故答案为：3．
14.【考点】垂径定理；勾股定理．
【分析】连接OD，先根据垂径定理得出PD=CD=4，再根据勾股定理求出OP的长，根据三角形的面积公式即可得出结论．
解：连接OD，
∵⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，CD=8，
∴PD=CD=4，
∴OP===3，
∴AP=OA+OP=5+3=8，
∴S△ACD=CD?AP=×8×8=32．
故答案为：32．
【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
15.【考点】垂径定理； 勾股定理； 等腰直角三角形．
【分析】连接OD，作OE⊥CD于E，由垂径定理得出CE=DE，证明△OEM是等腰直角三角形，由勾股定理得出OE=OM=，在Rt△ODE中，由勾股定理求出DE=，得出CD=2DE=即可．
解：连接OD，作OE⊥CD于E，如图所示：
则CE=DE，
∵AB是⊙O的直径，AB=4，点M是OA的中点，
∴OD=OA=2，OM=1，
∵∠OME=∠CMA=45°，
∴△OEM是等腰直角三角形，
∴OE=OM=，
在Rt△ODE中，由勾股定理得：DE==，
∴CD=2DE=；
故答案为：．
、解答题
16.【考点】垂径定理
【分析】过O作OE⊥AB，根据垂径定理得到AE=BE，CE=DE，从而得到AC=BD.
解：过O作OE⊥AB于点E，
则CE=DE，AE=BE，
∴BE-DE=AE-CE，即AC=BD；
17.【分析】（1）连接OM，由垂径定理可知MD=ND，在Rt△MOD中，已知OM、MD，易求OD．（2）利用锐角三角函数，易求∠OMD=30°，进而易求∠ACM=60°．
解：(1)连接OM. ∵点M是AB的中点，
∴OM⊥AB.过点O作OD⊥MN于点D，
由垂径定理，得MD=1/2MN=
∴在Rt△ODM中,OM=4,MD=
∴OD=2.
故圆心O到弦MN的距离为2
(2)cos∠OMD=MD:OM =,
∴∠OMD=30°,
∴∠ACM= 60°
18.【考点】垂径定理；勾股定理．
【分析】 先根据平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧得到CD⊥AB，然后在Rt△AOE中利用勾股定理计算OA即可．
解：连结OA，如图，
∵CD为直径，且CD平分AB于E，
∴CD⊥AB，AE=AB=4，
在Rt△AOE中，∵OE=3，AE=4，
∴OA==5，
∴⊙O的半径为5cm．
【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．也考查了勾股定理．
19.【考点】垂径定理
【分析】连OC，AB垂直于弦CD，由垂径定理得到PC=PD，得到PC=3；由P是OB的中点，则OC=2OP，得∠C=30°，PC=OP，则OP=，即可得到OC，AB．
解：连OC，如图，
∵AB垂直于弦CD，
∴PC=PD，
而CD=6cm，
∴PC=3cm，
又∵P是OB的中点，
∴OB=2OP，
∴OC=2OP，
∴∠C=30°，
∴PC=OP，则OP=cm，
∴OC=2OP=2cm，
所以直径AB的长为4 cm．
20.【考点】垂径定理；勾股定理．
【分析】过点O作OE⊥AB于点E，连接OB，由垂径定理可知AE=BE=AB，再根据勾股定理求出OE的长，由此可得出结论．
解：过点O作OE⊥AB于点E，连接OB，
∵AB=8cm，
∴AE=BE=AB=×8=4cm，
∵⊙O的直径为10cm，
∴OB=×10=5cm，
∴OE===3cm，
∵垂线段最短，半径最长，
∴3cm≤OP≤5cm．
【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
21.【考点】圆的切线的性质定理，垂径定理，多边形面积的计算。
解：（1）证明：ED与相切于D
F为弦AC的中点 ，
（2）解：①四边形DFAE为直角梯形，上底为AF，下底为DE，高为DF，有条件比较容易在直角三角形DOE中计算出DE长为，DF=，AF=，所以可以求出四边形DFAE的面积为；
②在三角形CDF中，，且DF=a/2, FC=AF=，进而可以求解在三角形CDF的面积为；
③四边形ACDE就是由四边形DFAE和三角形CDF组成的，进而可以得到四边形ACDE的面积就等于他们的面积和，为
（本题也可以通过证明四边形ACDE为平行四边形，进而通过平行四边形面积公式求解，主要思路合理即可）。