24.1.4 圆周角课时作业(1)
图片预览


文档简介
24.1.4 圆周角课时作业(1)
姓名:__________班级:__________考号:__________
一 、选择题
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.如图,△ABC内接于⊙O,∠A=50°,则∠OBC的度数为( )
A.40° B. 50° C. 80° D. 100°
3.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.120° B.140° C.150° D.160°
4.如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A.50° B. 80° C. 90° D. 100°
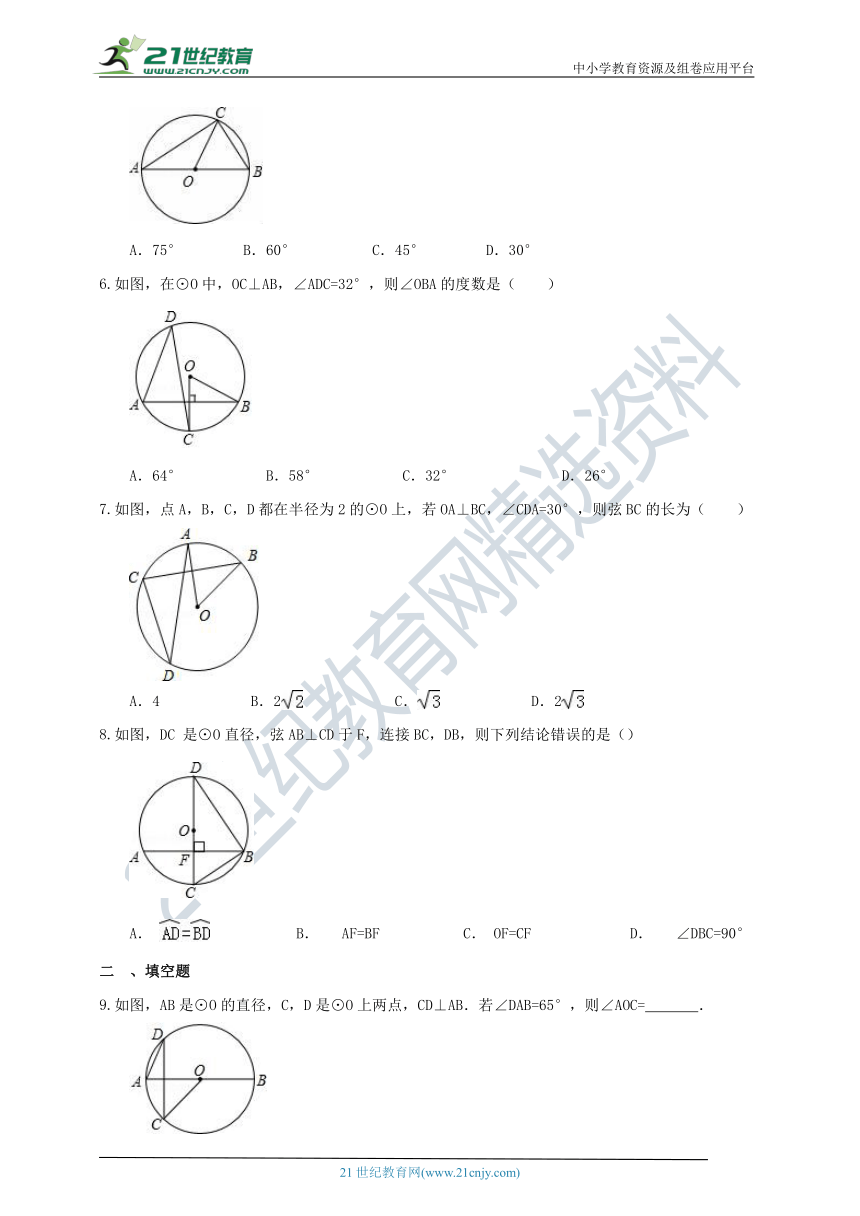
5.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
6.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )
A.64° B.58° C.32° D.26°
7.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( )
A.4 B.2 C. D.2
8.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()
A. B. AF=BF C. OF=CF D. ∠DBC=90°
二 、填空题
9.如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠AOC=.
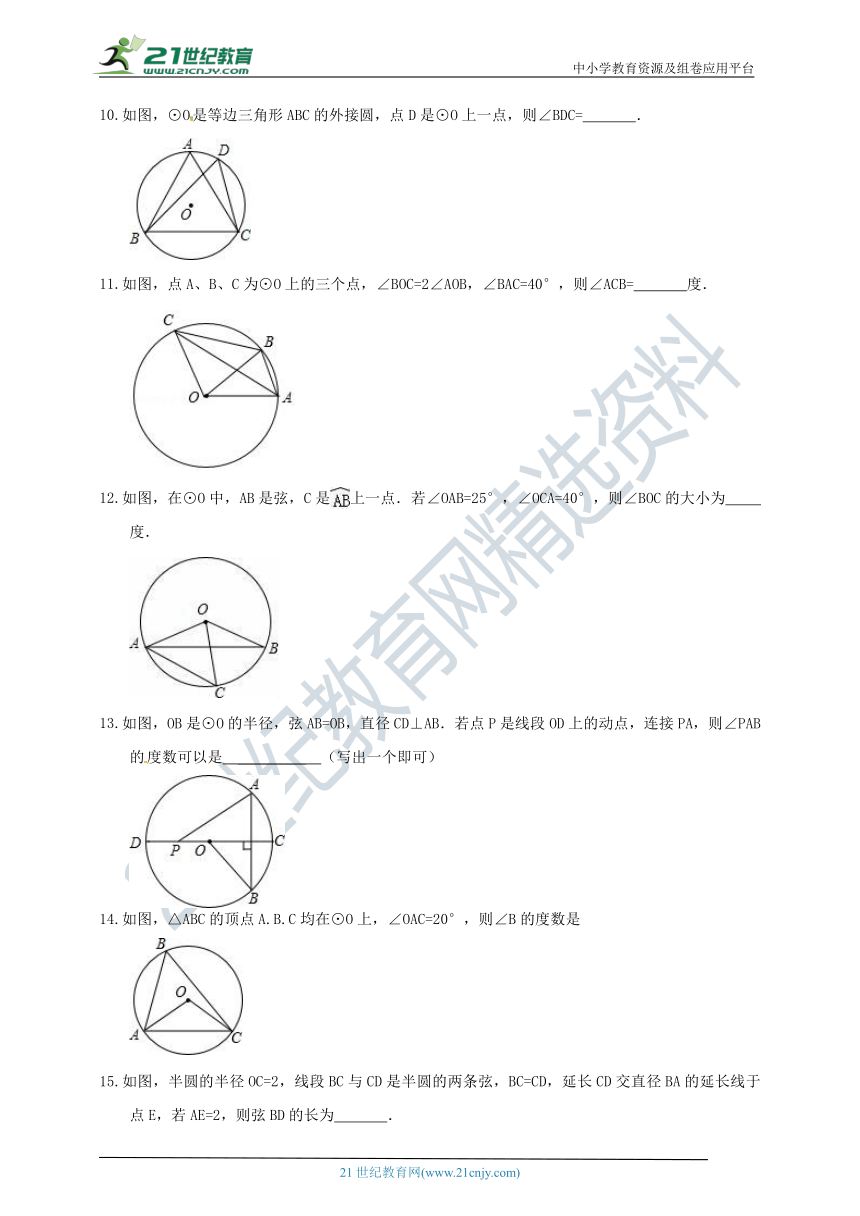
10.如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC=.
11.如图,点A、B、C为⊙O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB= 度.
12.如图,在⊙O中,AB是弦,C是上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为 度.
13.如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 _________ (写出一个即可)
14.如图,△ABC的顶点A.B.C均在⊙O上,∠OAC=20°,则∠B的度数是
15.如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
三 、解答题
16.如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
17.如图,在中,AB是的直径,与AC交于点D,,
求的度数;
18.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
19.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
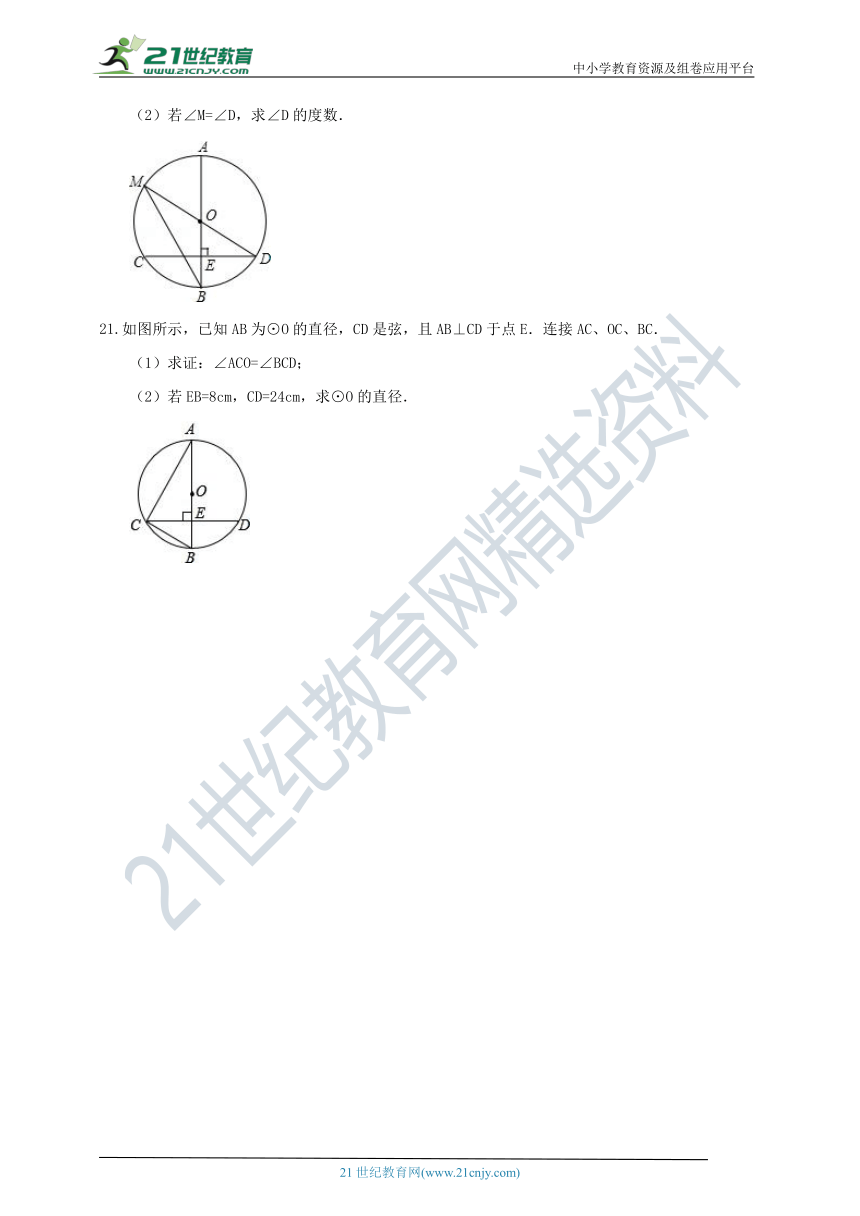
(2)若∠M=∠D,求∠D的度数.
21.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直径.
答案解析
一 、选择题
1.【考点】圆周角定理
【分析】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD的度数,再根据圆周角的性质,即可求得答案.
解:圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故选:D.
【点评】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.解:连接OC.
则∠BOC=2∠A=100°,
∵OB=OC,
∴∠OBC=∠OCB==40°.
故选A.
3.【考点】圆周角定理;垂径定理.
【分析】利用垂径定理得出==,进而求出∠BOD=40°,再利用邻补角的性质得出答案.
解:∵线段AB是⊙O的直径,弦CD丄AB,
∴=,
∵∠CAB=20°,
∴∠BOD=40°,
∴∠AOD=140°.
故选:B.
【点评】本题主要考查了圆周角定理以及垂径定理等知识,得出∠BOD的度数是解题关键.
4.解:∵∠ABC=50°,
∴∠AOC=2∠ABC=100°.
故选D.
5.【考点】圆周角定理.
【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
【点评】本题考查了圆周角定理以及角的计算,解题的关键是找出∠ACB=90°.本题属于基础题,难度不大,解决该题型题目时,找出直径所对的圆周角为90°是关键.
6.【考点】圆周角定理;全等三角形的判定与性质
【分析】根据垂径定理,可得=,∠OEB=90°,根据圆周角定理,可得∠3,根据直角三角形的性质,可得答案.
解:如图,
由OC⊥AB,得
=,∠OEB=90°.
∴∠2=∠3.
∵∠2=2∠1=2×32°=64°.
∴∠3=64°,
在Rt△OBE中,∠OEB=90°,
∴∠B=90°﹣∠3=90°﹣64°=26°,
故选:D.
【点评】本题考查了圆周角定理,利用垂径定理得出=,∠OEB=90°是解题关键,又利用了圆周角定理.
7.【考点】垂径定理;圆周角定理;圆内接四边形的性质
【分析】根据垂径定理得到CH=BH,=,根据圆周角定理求出∠AOB,根据正弦的定义求出BH,计算即可.
解:∵OA⊥BC,
∴CH=BH,=,
∴∠AOB=2∠CDA=60°,
∴BH=OB?sin∠AOB=,
∴BC=2BH=2,
故选:D.
【点评】本题考查的是垂径定理、圆周角定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
8.【考点】 垂径定理;圆心角、弧、弦的关系;圆周角定理.
【分析】 根据垂径定理可判断A、B,根据圆周角定理可判断D,继而可得出答案.
解:∵DC是⊙O直径,弦AB⊥CD于F,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
A、=,正确,故本选项错误;
B、AF=BF,正确,故本选项错误;
C、OF=CF,不能得出,错误,故本选项符合题意;
D、∠DBC=90°,正确,故本选项错误;
故选C.
【点评】 本题考查了垂径定理及圆周角定理,解答本题的关键是熟练掌握垂径定理、圆周角定理的内容,难度一般.
二 、填空题
9.【考点】 圆周角定理;垂径定理.
【分析】 由CD⊥AB.若∠DAB=65°,可求得∠D的度数,又由圆周角定理,即可求得∠AOC的度数,继而求得答案.
解:解:∵CD⊥AB.∠DAB=65°,
∴∠ADC=90°﹣∠DAB=25°,
∴∠AOC=2∠ADC=50°,
故答案为50°.
【点评】 本题考查了圆周角定理及垂径径定理.此题难度不大,注意掌握数形结合思想的应用.
10.【考点】 圆周角定理;等边三角形的性质.
【分析】 因为⊙O是等边三角形ABC的外接圆,所以∠A=∠ABC=∠ACB=60°,所以∠BCD=∠A=60°.
解:∵⊙O是等边三角形ABC的外接圆,
∴∠A=∠ABC=∠ACB=60°,
∴∠BDC=∠A=60°.
【点评】 此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
11.【考点】圆周角定理.
【分析】根据圆周角定理即可得到结论.
解:∵∠BAC=BOC,∠ACB=AOB,
∵∠BOC=2∠AOB,
∴∠ACB=BAC=20°.
故答案为:20.
12.【考点】圆周角定理.
【分析】由∠BAO=25°,利用等腰三角形的性质,可求得∠AOB的度数,又由∠OCA=40°,可求得∠CAO的度数,继而求得∠AOC的度数,则可求得答案.
解:∵∠BAO=25°,OA=OB,
∴∠B=∠BAO=25°,
∴∠AOB=180°﹣∠BAO﹣∠B=130°,
∵∠ACO=40°,OA=OC,
∴∠C=∠CAO=40°,
∴∠AOC=180°﹣∠CAO﹣∠C=100°,
∴∠BOC=∠AOB﹣∠AOC=30°.
故答案为30°.
【点评】本题考查了圆周角定理以及等腰三角形的性质.注意利用等腰三角形的性质求解是关键.
13.【考点】圆周角定理;等腰三角形的性质;垂径定理.
【分析】当P点与D点重合是∠DAB=75°,与O重合则OAB=60°,∠OAB≤∠PAB≤∠DAB,所以∠PAB的度数可以是60°﹣﹣75°之间的任意数.
解:连接DA,OA,则△OAB是等边三角形,
∴∠OAB=∠AOB=60°,
∵DC是直径,DC⊥AB,
∴∠AOC=∠AOB=30°,
∴∠ADC=15°,
∴∠DAB=75°,
∵,∠OAB≤∠PAB≤∠DAB,
∴∠PAB的度数可以是60°﹣75°之间的任意数.
故答案为:70°
【点评】本题考查了垂径定理,等边三角形的判定及性质,等腰三角形的判定及性质.
14.【考点】圆周角定理
【分析】 先根据等腰三角形的性质求出∠ACO的度数,再由三角形内角和定理求出∠AOC的度数,由圆周角定理∠B的度数即可.
解:∵OA=OC,∠OAC=20°,
∴∠ACO=∠OAC=20°,
∴∠AOC=180°-∠ACO-∠OAC=180°-20°-20°=140°,
∴∠B=∠AOC=×140°=70°.
故答案为:70°.
15.【考点】勾股定理的应用;圆心角、弧、弦的关系;圆周角定理
【分析】连接OD,AD,根据OC平分∠BCD,BC=DC,即可得到BD⊥CO,依据AB是直径,可得AD⊥BD,进而得出AD=CO=1,再根据Rt△ABD,利用勾股定理可得BD=.
解:如图,连接OD,AD,
∵BC=DC,BO=DO,
∴∠BDC=∠DBC,∠BDO=∠DBO,
∴∠CDO=∠CBO,
又∵OC=OB=OD,
∴∠BCO=∠DCO,即OC平分∠BCD,
又∵BC=DC,
∴BD⊥CO,
又∵AB是直径,
∴AD⊥BD,
∴AD∥CO,
又∵AE=AO=2,
∴AD=CO=1,
∴Rt△ABD中,BD===.
故答案为:.
【点评】本题主要考查了圆周角定理以及勾股定理的综合运用,半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握.
三 、解答题
16.【考点】圆周角定理.
【分析】根据直径所对的圆周角是直角,构造直角三角形ABD,再根据同弧所对的圆周角相等,求得∠B的度数,即可求得∠BAD的度数.
解:∵AB为⊙O直径
∴∠ADB=90°
∵相同的弧所对应的圆周角相等,且∠ACD=25°
∴∠B=25°
∴∠BAD=90°﹣∠B=65°.
17.【考点】角形内角和定理及圆周角定理
【分析】先根据三角形内角和定理求出∠A的度数,再由圆周角定理即可求解.
解:在△ABC中,∵∠B=60°,∠C=75°, ∴∠A=45°. ∵AB是⊙O的直径,⊙O与AC交于点D, ∴∠DOB=2∠A=90°. 故答案为:90°. 【点评】本题考查的是三角形内角和定理及圆周角定理,比较简单
18.【考点】圆周角定理;等腰三角形的判定与性质;勾股定理.
【分析】(1)由等腰三角形的性质得到∠EDC=∠C,由圆外接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,由“三线合一”定理得到BE=CE=BC=,由割线定理可证得结论.
(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=BC=,
∵CE?CB=CD?CA,AC=AB=4,
∴?2=4CD,
∴CD=.
【点评】本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
19.【考点】圆周角定理;平行线的性质;三角形中位线定理.
【分析】(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO===55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
【点评】本题考查了圆周角定理以及三角形的中位线定理,正确证明OE是△ABC的中位线是关键.
20.【考点】垂径定理;勾股定理;圆周角定理.
【分析】(1)先根据CD=16,BE=4,得出OE的长,进而得出OB的长,进而得出结论;
(2)由∠M=∠D,∠DOB=2∠D,结合直角三角形可以求得结果;
解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
【点评】本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;
21.【考点】 垂径定理;勾股定理;圆周角定理.
【分析】 (1)根据垂径定理和圆的性质,同弧的圆周角相等,又因为△AOC是等腰三角形,即可求证.
(2)根据勾股定理,求出各边之间的关系,即可确定半径.
(1)证明:连接OC,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于E,
∴CE=ED,.
∴∠BCD=∠BAC.
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD.
(2)解:设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣8)cm,
CE=CD=×24=12cm,(6分)
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R﹣8)2+122(8分)
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.
【点评】 本题考查垂弦定理、圆心角、圆周角的应用能力.
姓名:__________班级:__________考号:__________
一 、选择题
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.如图,△ABC内接于⊙O,∠A=50°,则∠OBC的度数为( )
A.40° B. 50° C. 80° D. 100°
3.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.120° B.140° C.150° D.160°
4.如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A.50° B. 80° C. 90° D. 100°
5.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
6.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )
A.64° B.58° C.32° D.26°
7.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( )
A.4 B.2 C. D.2
8.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()
A. B. AF=BF C. OF=CF D. ∠DBC=90°
二 、填空题
9.如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠AOC=.
10.如图,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC=.
11.如图,点A、B、C为⊙O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB= 度.
12.如图,在⊙O中,AB是弦,C是上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的大小为 度.
13.如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 _________ (写出一个即可)
14.如图,△ABC的顶点A.B.C均在⊙O上,∠OAC=20°,则∠B的度数是
15.如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为 .
三 、解答题
16.如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
17.如图,在中,AB是的直径,与AC交于点D,,
求的度数;
18.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
19.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
21.如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直径.
答案解析
一 、选择题
1.【考点】圆周角定理
【分析】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD的度数,再根据圆周角的性质,即可求得答案.
解:圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故选:D.
【点评】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.解:连接OC.
则∠BOC=2∠A=100°,
∵OB=OC,
∴∠OBC=∠OCB==40°.
故选A.
3.【考点】圆周角定理;垂径定理.
【分析】利用垂径定理得出==,进而求出∠BOD=40°,再利用邻补角的性质得出答案.
解:∵线段AB是⊙O的直径,弦CD丄AB,
∴=,
∵∠CAB=20°,
∴∠BOD=40°,
∴∠AOD=140°.
故选:B.
【点评】本题主要考查了圆周角定理以及垂径定理等知识,得出∠BOD的度数是解题关键.
4.解:∵∠ABC=50°,
∴∠AOC=2∠ABC=100°.
故选D.
5.【考点】圆周角定理.
【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
【点评】本题考查了圆周角定理以及角的计算,解题的关键是找出∠ACB=90°.本题属于基础题,难度不大,解决该题型题目时,找出直径所对的圆周角为90°是关键.
6.【考点】圆周角定理;全等三角形的判定与性质
【分析】根据垂径定理,可得=,∠OEB=90°,根据圆周角定理,可得∠3,根据直角三角形的性质,可得答案.
解:如图,
由OC⊥AB,得
=,∠OEB=90°.
∴∠2=∠3.
∵∠2=2∠1=2×32°=64°.
∴∠3=64°,
在Rt△OBE中,∠OEB=90°,
∴∠B=90°﹣∠3=90°﹣64°=26°,
故选:D.
【点评】本题考查了圆周角定理,利用垂径定理得出=,∠OEB=90°是解题关键,又利用了圆周角定理.
7.【考点】垂径定理;圆周角定理;圆内接四边形的性质
【分析】根据垂径定理得到CH=BH,=,根据圆周角定理求出∠AOB,根据正弦的定义求出BH,计算即可.
解:∵OA⊥BC,
∴CH=BH,=,
∴∠AOB=2∠CDA=60°,
∴BH=OB?sin∠AOB=,
∴BC=2BH=2,
故选:D.
【点评】本题考查的是垂径定理、圆周角定理,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
8.【考点】 垂径定理;圆心角、弧、弦的关系;圆周角定理.
【分析】 根据垂径定理可判断A、B,根据圆周角定理可判断D,继而可得出答案.
解:∵DC是⊙O直径,弦AB⊥CD于F,
∴点D是优弧AB的中点,点C是劣弧AB的中点,
A、=,正确,故本选项错误;
B、AF=BF,正确,故本选项错误;
C、OF=CF,不能得出,错误,故本选项符合题意;
D、∠DBC=90°,正确,故本选项错误;
故选C.
【点评】 本题考查了垂径定理及圆周角定理,解答本题的关键是熟练掌握垂径定理、圆周角定理的内容,难度一般.
二 、填空题
9.【考点】 圆周角定理;垂径定理.
【分析】 由CD⊥AB.若∠DAB=65°,可求得∠D的度数,又由圆周角定理,即可求得∠AOC的度数,继而求得答案.
解:解:∵CD⊥AB.∠DAB=65°,
∴∠ADC=90°﹣∠DAB=25°,
∴∠AOC=2∠ADC=50°,
故答案为50°.
【点评】 本题考查了圆周角定理及垂径径定理.此题难度不大,注意掌握数形结合思想的应用.
10.【考点】 圆周角定理;等边三角形的性质.
【分析】 因为⊙O是等边三角形ABC的外接圆,所以∠A=∠ABC=∠ACB=60°,所以∠BCD=∠A=60°.
解:∵⊙O是等边三角形ABC的外接圆,
∴∠A=∠ABC=∠ACB=60°,
∴∠BDC=∠A=60°.
【点评】 此题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
11.【考点】圆周角定理.
【分析】根据圆周角定理即可得到结论.
解:∵∠BAC=BOC,∠ACB=AOB,
∵∠BOC=2∠AOB,
∴∠ACB=BAC=20°.
故答案为:20.
12.【考点】圆周角定理.
【分析】由∠BAO=25°,利用等腰三角形的性质,可求得∠AOB的度数,又由∠OCA=40°,可求得∠CAO的度数,继而求得∠AOC的度数,则可求得答案.
解:∵∠BAO=25°,OA=OB,
∴∠B=∠BAO=25°,
∴∠AOB=180°﹣∠BAO﹣∠B=130°,
∵∠ACO=40°,OA=OC,
∴∠C=∠CAO=40°,
∴∠AOC=180°﹣∠CAO﹣∠C=100°,
∴∠BOC=∠AOB﹣∠AOC=30°.
故答案为30°.
【点评】本题考查了圆周角定理以及等腰三角形的性质.注意利用等腰三角形的性质求解是关键.
13.【考点】圆周角定理;等腰三角形的性质;垂径定理.
【分析】当P点与D点重合是∠DAB=75°,与O重合则OAB=60°,∠OAB≤∠PAB≤∠DAB,所以∠PAB的度数可以是60°﹣﹣75°之间的任意数.
解:连接DA,OA,则△OAB是等边三角形,
∴∠OAB=∠AOB=60°,
∵DC是直径,DC⊥AB,
∴∠AOC=∠AOB=30°,
∴∠ADC=15°,
∴∠DAB=75°,
∵,∠OAB≤∠PAB≤∠DAB,
∴∠PAB的度数可以是60°﹣75°之间的任意数.
故答案为:70°
【点评】本题考查了垂径定理,等边三角形的判定及性质,等腰三角形的判定及性质.
14.【考点】圆周角定理
【分析】 先根据等腰三角形的性质求出∠ACO的度数,再由三角形内角和定理求出∠AOC的度数,由圆周角定理∠B的度数即可.
解:∵OA=OC,∠OAC=20°,
∴∠ACO=∠OAC=20°,
∴∠AOC=180°-∠ACO-∠OAC=180°-20°-20°=140°,
∴∠B=∠AOC=×140°=70°.
故答案为:70°.
15.【考点】勾股定理的应用;圆心角、弧、弦的关系;圆周角定理
【分析】连接OD,AD,根据OC平分∠BCD,BC=DC,即可得到BD⊥CO,依据AB是直径,可得AD⊥BD,进而得出AD=CO=1,再根据Rt△ABD,利用勾股定理可得BD=.
解:如图,连接OD,AD,
∵BC=DC,BO=DO,
∴∠BDC=∠DBC,∠BDO=∠DBO,
∴∠CDO=∠CBO,
又∵OC=OB=OD,
∴∠BCO=∠DCO,即OC平分∠BCD,
又∵BC=DC,
∴BD⊥CO,
又∵AB是直径,
∴AD⊥BD,
∴AD∥CO,
又∵AE=AO=2,
∴AD=CO=1,
∴Rt△ABD中,BD===.
故答案为:.
【点评】本题主要考查了圆周角定理以及勾股定理的综合运用,半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握.
三 、解答题
16.【考点】圆周角定理.
【分析】根据直径所对的圆周角是直角,构造直角三角形ABD,再根据同弧所对的圆周角相等,求得∠B的度数,即可求得∠BAD的度数.
解:∵AB为⊙O直径
∴∠ADB=90°
∵相同的弧所对应的圆周角相等,且∠ACD=25°
∴∠B=25°
∴∠BAD=90°﹣∠B=65°.
17.【考点】角形内角和定理及圆周角定理
【分析】先根据三角形内角和定理求出∠A的度数,再由圆周角定理即可求解.
解:在△ABC中,∵∠B=60°,∠C=75°, ∴∠A=45°. ∵AB是⊙O的直径,⊙O与AC交于点D, ∴∠DOB=2∠A=90°. 故答案为:90°. 【点评】本题考查的是三角形内角和定理及圆周角定理,比较简单
18.【考点】圆周角定理;等腰三角形的判定与性质;勾股定理.
【分析】(1)由等腰三角形的性质得到∠EDC=∠C,由圆外接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,由“三线合一”定理得到BE=CE=BC=,由割线定理可证得结论.
(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=BC=,
∵CE?CB=CD?CA,AC=AB=4,
∴?2=4CD,
∴CD=.
【点评】本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
19.【考点】圆周角定理;平行线的性质;三角形中位线定理.
【分析】(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO===55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
【点评】本题考查了圆周角定理以及三角形的中位线定理,正确证明OE是△ABC的中位线是关键.
20.【考点】垂径定理;勾股定理;圆周角定理.
【分析】(1)先根据CD=16,BE=4,得出OE的长,进而得出OB的长,进而得出结论;
(2)由∠M=∠D,∠DOB=2∠D,结合直角三角形可以求得结果;
解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
【点评】本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;
21.【考点】 垂径定理;勾股定理;圆周角定理.
【分析】 (1)根据垂径定理和圆的性质,同弧的圆周角相等,又因为△AOC是等腰三角形,即可求证.
(2)根据勾股定理,求出各边之间的关系,即可确定半径.
(1)证明:连接OC,
∵AB为⊙O的直径,CD是弦,且AB⊥CD于E,
∴CE=ED,.
∴∠BCD=∠BAC.
∵OA=OC,∴∠OAC=∠OCA.
∴∠ACO=∠BCD.
(2)解:设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣8)cm,
CE=CD=×24=12cm,(6分)
在Rt△CEO中,由勾股定理可得
OC2=OE2+CE2,即R2=(R﹣8)2+122(8分)
解得R=13,∴2R=2×13=26cm.
答:⊙O的直径为26cm.
【点评】 本题考查垂弦定理、圆心角、圆周角的应用能力.
同课章节目录
