24.1.2 垂直于弦的直径课时作业(2)
文档属性
| 名称 | 24.1.2 垂直于弦的直径课时作业(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 00:00:00 | ||
图片预览



文档简介
24.1.2 垂直于弦的直径课时作业(2)
姓名:__________班级:__________考号:__________
一 、选择题
1.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B. cm C. D.
2.一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
A.4 B.6 C.8 D.9
3.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm B.16cm C.24cm D.26cm
4.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的
算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,
以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,
不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,
问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片
到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A. 2 B. C. 2 D. 3
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油
面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A. 6分米 B. 8分米 C. 10分米 D. 12分米
7.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2米 B.2.5米 C.2.4米 D.2.1米
二 、填空题
8.某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为 m.
9.如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
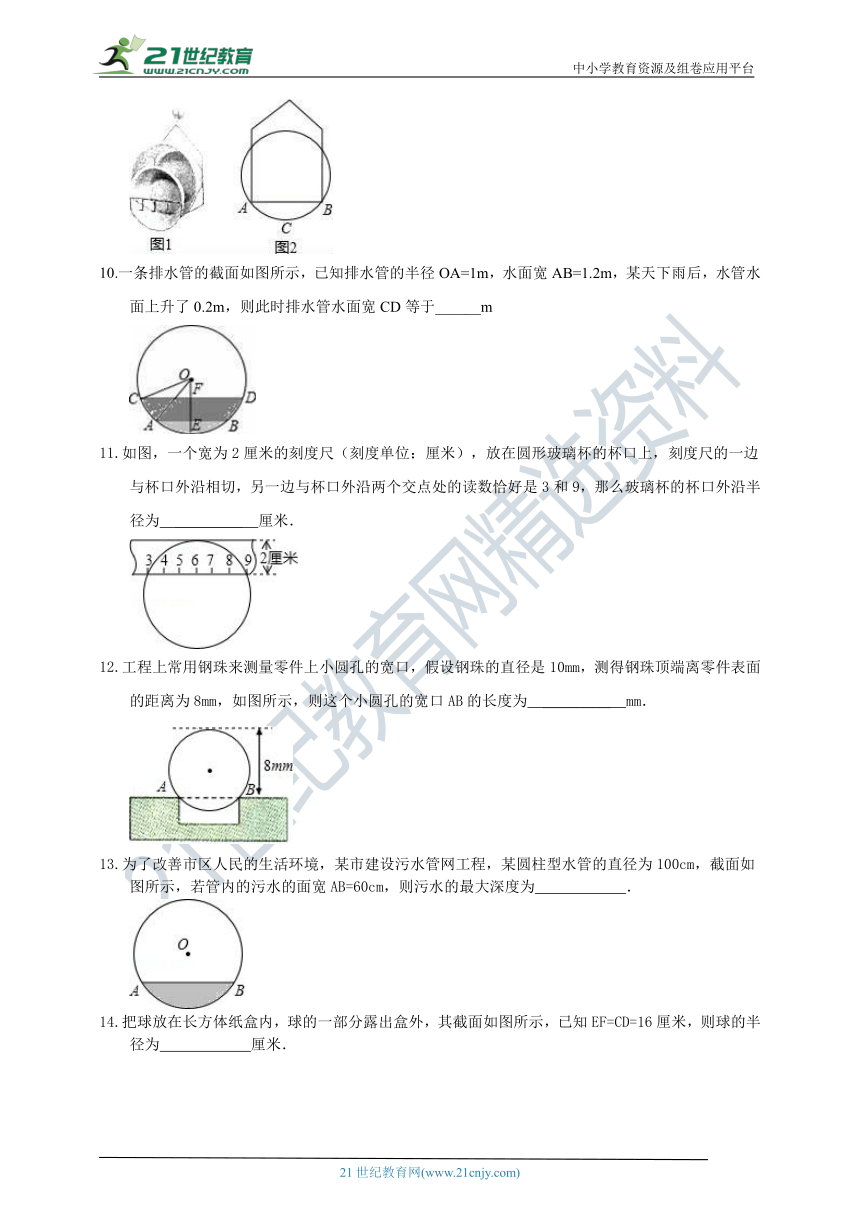
10.一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于______m
11.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 _________ 厘米.
12.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 _________ mm.
13.为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为 .
14.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
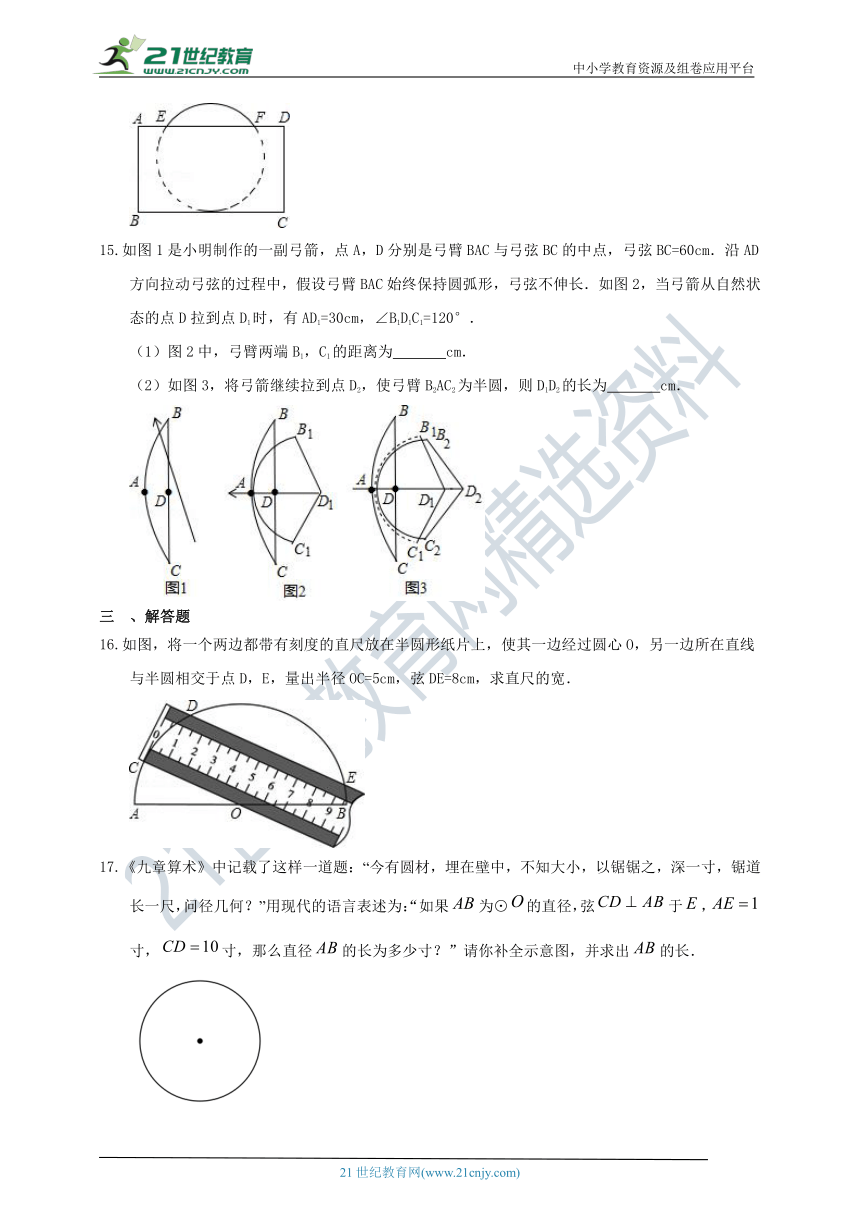
15.如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 cm.
三 、解答题
16.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
17.《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果为⊙的直径,弦于,寸,寸,那么直径的长为多少寸?”请你补全示意图,并求出的长.
18.如图,一条公路的转弯处是一段圆弧().
(1)用直尺和圆规作出所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若的中点C到弦AB的距离为20m,AB=80m,求所在圆的半径.
19.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
答案解析
一 、选择题
1.【考点】垂径定理;勾股定理.
【分析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.
解:作OD⊥AB于D,连接OA.
根据题意得:OD=OA=1cm,
再根据勾股定理得:AD=cm,
根据垂径定理得:AB=2cm.
故选:C.
【点评】注意由题目中的折叠即可发现OD=OA=1.考查了勾股定理以及垂径定理.
2.【考点】垂径定理的应用;勾股定理.
【分析】因为M是⊙O弦CD的中点,根据垂径定理,EM⊥CD,则CM=DM=3,在Rt△COM中,有OC2=CM2+OM2,可求得OM,进而就可求得EM.
解:∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=6则有:CM=CD=3,
设OM是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:52=32+x2,
解得:x=4,
所以EM=5+4=9.
故选D.
【点评】此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+()2成立,知道这三个量中的任意两个,就可以求出另外一个.
3.【考点】垂径定理的应用.
【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.
解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
4.【考点】垂径定理的应用
【分析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解方程即可;
解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
【点评】本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
5.【考点】垂径定理的应用;勾股定理.
【分析】在网格中找点A、B、D(如图),作AB,BD的中垂线,交点O就是圆心,故OA即为此圆的半径,根据勾股定理求出OA的长即可.
解:如图所示,作AB,BD的中垂线,交点O就是圆心.
连接OA、OB,
∵OC⊥AB,OA=OB
∴O即为此圆形镜子的圆心,
∵AC=1,OC=2,
∴OA===.
故选B.
【点评】本题考查的是垂径定理在实际生活中的运用,根据题意构造出直角三角形是解答此题的关键.
6.【考点】垂径定理的应用.
【分析】如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=AB=3,CF=CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=AB=3,CF=CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA==5,
∴直径MN=2OA=10分米.
故选C.
【点评】本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.
7.【考点】垂径定理的应用.
【分析】连接OF,交AC于点E,设圆O的半径为R米,根据勾股定理列出方程,解方程即可.
解:连接OF,交AC于点E,
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE===0.75米,
OE=R﹣AB=R﹣0.25,
∵AE2+OE2=OA2,
∴0.752+(R﹣0.25)2=R2,
解得R=1.25.
1.25×2=2.5(米).
答:这扇圆弧形门的最高点离地面的距离是2.5米.
故选:B.
【点评】本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.
二 、填空题
8.【考点】垂径定理的应用;勾股定理.
【分析】先设出圆弧形屋顶所在圆的半径为O,所在圆的半径为r,过O作OD⊥AB交⊙O于点C,再利用勾股定理可得问题答案.
解:设圆弧形屋顶所在圆的半径为O,所在圆的半径为r,
过O作OD⊥AB交⊙O于点C.
由题意可知CD=20m,
在Rt△BOD中,B02=OD2+BD2,
r2=(r﹣20)2+402,得r=50.
故答案为50.
【点评】本题考查垂径定理.解题思路:有关弦的问题常作弦心距,构造直角三角形利用勾股定理解决.在解题过程中要注意列方程的方法.
9.【考点】垂径定理的应用.
【分析】设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,在RT△AOD中利用勾股定理即可解决问题.
解;如图,设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,
∵OC⊥AB,
∵AD=DB=AB=20,
在RT△AOD中,∵∠ADO=90°,
∴OA2=OD2+AD2,
∴R2=202+(R﹣10)2,
∴R=25.
故答案为25.
10.【考点】垂径定理的应用;勾股定理.
【分析】先根据勾股定理求出OE的长,再根据垂径定理求出CF的长,即可得出结论.
解:如图:
∵AB=1.2m,OE⊥AB,OA=1m,
∴OE=0.8m,
∵水管水面上升了0.2m,
∴OF=0.8﹣0.2=0.6m,
∴CF=m,
∴CD=1.6m.
故答案为:1.6.
11.【考点】垂径定理的应用;勾股定理.
【分析】先求出弦AC的长,再过点O作OB⊥AC于点B,由垂径定理可得出AB的长,设杯口的半径为r,则OB=r﹣2,OA=r,在Rt△AOB中根据勾股定理求出r的值即可.
解:∵杯口外沿两个交点处的读数恰好是3和9,
∴AC=9﹣3=6,
过点O作OB⊥AC于点B,则AB=AC=×6=3cm,
设杯口的半径为r,则OB=r﹣2,OA=r,
在Rt△AOB中,
OA2=OB2+AB2,即r2=(r﹣2)2+32,
解得r=cm.
故答案为:.
【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
12.【考点】垂径定理的应用;勾股定理.
【分析】先求出钢珠的半径及OD的长,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD的长,进而得出AB的长.
解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,
∴AB=2AD=2×4=8mm.
故答案为:8.
【点评】本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
13.【考点】垂径定理的应用;勾股定理.
【分析】首先连接OA,过点O作OE⊥AB,交⊙O于F,根据垂径定理,即可求得AE的值,然后在Rt△OAE中,利用勾股定理,即可求得OE的值,继而求得污水的最大深度.
解:连接OA,过点O作OE⊥AB,交⊙O于F,
∵圆柱型水管的直径为100cm,
∴AO=FO=50cm,
∵AB=60cm,
∴AE=30cm,
∴OE===40(cm),
∴EF=50﹣40=10(cm),
故答案为:10cm.
【点评】此题主要考查了勾股定理和垂径定理的应用,此类题要构造一个由半径、半弦、弦心距组成的直角三角形,然后根据勾股定理以及垂径定理进行计算.
14.考点: 垂径定理的应用;勾股定理.
分析: 首先找到EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM是16﹣x,MF=8,然后在直角三角形MOF中利用勾股定理求得OF的长即可.
解答: 解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
设OF=x,则OM=16﹣x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2
即:(16﹣x)2+82=x2
解得:x=10
故答案为:10.
点评: 本题考查了垂径定理及勾股定理的知识,解题的关键是正确的作出辅助线构造直角三角形.
15.【考点】勾股定理的应用;垂径定理的应用
【分析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
解:(1)如图2中,连接B1C1交DD1于H.
∵D1A=D1B1=30
∴D1是的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15,
∴B1C1=30
∴弓臂两端B1,C1的距离为30
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=,
∴r=20,
∴AG=GB2=20,GD1=30﹣20=10,
在Rt△GB2D2中,GD2==10
∴D1D2=10﹣10.
故答案为30,10﹣10,
【点评】本题考查垂径定理的应用、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.
三 、解答题
16.【考点】垂径定理的应用;勾股定理.
【分析】过点O作OM⊥DE于点M,连接OD.
根据垂径定理“垂直于弦的直径平分弦,并且平分弦所对的两条弧”和勾股定理进行计算.
解:过点O作OM⊥DE于点M,连接OD.
∴DM=.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
【点评】综合运用了垂径定理和勾股定理.
17.【考点】垂径定理的应用,勾股定理
【分析】连接OD,由直径AB与弦CD垂直,根据垂径定理得到E为CD的中点,由CD的长求出DE的长,设OD=OA=r寸,则AB=2r寸,OE=(r﹣1)寸,由勾股定理得出方程,解方程求出半径,即可得出直径AB的长.?
解:示意图如图所示, 连接OC
∵AB为⊙O的直径,且CD⊥AB于点E,CD=10,
∴CE=CD=5 .
∵AE=1 ,
设⊙O的半径为r寸, 则OE 为r-1寸
在Rt△CEO中,由勾股定理得
解得r=13,
∴ 直径AB的长为26寸.
18.【考点】作图—复杂作图;勾股定理;垂径定理的应用.
【分析】(1)连结AC、BC,分别作AC和BC的垂直平分线,两垂直平分线的交点为点O,如图1;
(2)连接OA,OC,OC交AB于D,如图2,根据垂径定理的推论,由C为的中点得到OC⊥AB,AD=BD=AB=40,则CD=20,设⊙O的半径为r,在Rt△OAD中利用勾股定理得到r2=(r﹣20)2+402,然后解方程即可.
解:(1)如图1,
点O为所求;
(2)连接OA,OC,OC交AB于D,如图2,
∵C为的中点,
∴OC⊥AB,
∴AD=BD=AB=40,
设⊙O的半径为r,则OA=r,OD=OD﹣CD=r﹣20,
在Rt△OAD中,∵OA2=OD2+AD2,
∴r2=(r﹣20)2+402,解得r=50,
即所在圆的半径是50m.
19.【考点】勾股定理;垂径定理的应用.
【分析】(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
解:(1)作BH⊥PQ于点H.
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°﹣45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2=2=200,
∴台风影响的时间t==5(小时).
故B市受台风影响的时间为5小时.
【点评】本题考查的是直角三角形的性质及垂径定理在实际生活中的运用,解答此题的关键是构造出直角三角形及圆.
姓名:__________班级:__________考号:__________
一 、选择题
1.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B. cm C. D.
2.一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
A.4 B.6 C.8 D.9
3.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm B.16cm C.24cm D.26cm
4.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的
算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,
以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,
不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,
问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片
到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A. 2 B. C. 2 D. 3
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油
面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A. 6分米 B. 8分米 C. 10分米 D. 12分米
7.如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2米 B.2.5米 C.2.4米 D.2.1米
二 、填空题
8.某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为 m.
9.如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
10.一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于______m
11.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 _________ 厘米.
12.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 _________ mm.
13.为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图所示,若管内的污水的面宽AB=60cm,则污水的最大深度为 .
14.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
15.如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为 cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为 cm.
三 、解答题
16.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
17.《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果为⊙的直径,弦于,寸,寸,那么直径的长为多少寸?”请你补全示意图,并求出的长.
18.如图,一条公路的转弯处是一段圆弧().
(1)用直尺和圆规作出所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若的中点C到弦AB的距离为20m,AB=80m,求所在圆的半径.
19.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
答案解析
一 、选择题
1.【考点】垂径定理;勾股定理.
【分析】在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.
解:作OD⊥AB于D,连接OA.
根据题意得:OD=OA=1cm,
再根据勾股定理得:AD=cm,
根据垂径定理得:AB=2cm.
故选:C.
【点评】注意由题目中的折叠即可发现OD=OA=1.考查了勾股定理以及垂径定理.
2.【考点】垂径定理的应用;勾股定理.
【分析】因为M是⊙O弦CD的中点,根据垂径定理,EM⊥CD,则CM=DM=3,在Rt△COM中,有OC2=CM2+OM2,可求得OM,进而就可求得EM.
解:∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=6则有:CM=CD=3,
设OM是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:52=32+x2,
解得:x=4,
所以EM=5+4=9.
故选D.
【点评】此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+()2成立,知道这三个量中的任意两个,就可以求出另外一个.
3.【考点】垂径定理的应用.
【分析】首先构造直角三角形,再利用勾股定理得出BC的长,进而根据垂径定理得出答案.
解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8,OD=13,
∴OC=5,
又∵OB=13,
∴Rt△BCO中,BC==12,
∴AB=2BC=24.
故选:C.
4.【考点】垂径定理的应用
【分析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r﹣1,OA=r,则有r2=52+(r﹣1)2,解方程即可;
解:设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
【点评】本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
5.【考点】垂径定理的应用;勾股定理.
【分析】在网格中找点A、B、D(如图),作AB,BD的中垂线,交点O就是圆心,故OA即为此圆的半径,根据勾股定理求出OA的长即可.
解:如图所示,作AB,BD的中垂线,交点O就是圆心.
连接OA、OB,
∵OC⊥AB,OA=OB
∴O即为此圆形镜子的圆心,
∵AC=1,OC=2,
∴OA===.
故选B.
【点评】本题考查的是垂径定理在实际生活中的运用,根据题意构造出直角三角形是解答此题的关键.
6.【考点】垂径定理的应用.
【分析】如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=AB=3,CF=CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=AB=3,CF=CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA==5,
∴直径MN=2OA=10分米.
故选C.
【点评】本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.
7.【考点】垂径定理的应用.
【分析】连接OF,交AC于点E,设圆O的半径为R米,根据勾股定理列出方程,解方程即可.
解:连接OF,交AC于点E,
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE===0.75米,
OE=R﹣AB=R﹣0.25,
∵AE2+OE2=OA2,
∴0.752+(R﹣0.25)2=R2,
解得R=1.25.
1.25×2=2.5(米).
答:这扇圆弧形门的最高点离地面的距离是2.5米.
故选:B.
【点评】本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.
二 、填空题
8.【考点】垂径定理的应用;勾股定理.
【分析】先设出圆弧形屋顶所在圆的半径为O,所在圆的半径为r,过O作OD⊥AB交⊙O于点C,再利用勾股定理可得问题答案.
解:设圆弧形屋顶所在圆的半径为O,所在圆的半径为r,
过O作OD⊥AB交⊙O于点C.
由题意可知CD=20m,
在Rt△BOD中,B02=OD2+BD2,
r2=(r﹣20)2+402,得r=50.
故答案为50.
【点评】本题考查垂径定理.解题思路:有关弦的问题常作弦心距,构造直角三角形利用勾股定理解决.在解题过程中要注意列方程的方法.
9.【考点】垂径定理的应用.
【分析】设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,在RT△AOD中利用勾股定理即可解决问题.
解;如图,设圆的圆心为O,连接OA,OC,OC与AB交于点D,设⊙O半径为R,
∵OC⊥AB,
∵AD=DB=AB=20,
在RT△AOD中,∵∠ADO=90°,
∴OA2=OD2+AD2,
∴R2=202+(R﹣10)2,
∴R=25.
故答案为25.
10.【考点】垂径定理的应用;勾股定理.
【分析】先根据勾股定理求出OE的长,再根据垂径定理求出CF的长,即可得出结论.
解:如图:
∵AB=1.2m,OE⊥AB,OA=1m,
∴OE=0.8m,
∵水管水面上升了0.2m,
∴OF=0.8﹣0.2=0.6m,
∴CF=m,
∴CD=1.6m.
故答案为:1.6.
11.【考点】垂径定理的应用;勾股定理.
【分析】先求出弦AC的长,再过点O作OB⊥AC于点B,由垂径定理可得出AB的长,设杯口的半径为r,则OB=r﹣2,OA=r,在Rt△AOB中根据勾股定理求出r的值即可.
解:∵杯口外沿两个交点处的读数恰好是3和9,
∴AC=9﹣3=6,
过点O作OB⊥AC于点B,则AB=AC=×6=3cm,
设杯口的半径为r,则OB=r﹣2,OA=r,
在Rt△AOB中,
OA2=OB2+AB2,即r2=(r﹣2)2+32,
解得r=cm.
故答案为:.
【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
12.【考点】垂径定理的应用;勾股定理.
【分析】先求出钢珠的半径及OD的长,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD的长,进而得出AB的长.
解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,
∴AB=2AD=2×4=8mm.
故答案为:8.
【点评】本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
13.【考点】垂径定理的应用;勾股定理.
【分析】首先连接OA,过点O作OE⊥AB,交⊙O于F,根据垂径定理,即可求得AE的值,然后在Rt△OAE中,利用勾股定理,即可求得OE的值,继而求得污水的最大深度.
解:连接OA,过点O作OE⊥AB,交⊙O于F,
∵圆柱型水管的直径为100cm,
∴AO=FO=50cm,
∵AB=60cm,
∴AE=30cm,
∴OE===40(cm),
∴EF=50﹣40=10(cm),
故答案为:10cm.
【点评】此题主要考查了勾股定理和垂径定理的应用,此类题要构造一个由半径、半弦、弦心距组成的直角三角形,然后根据勾股定理以及垂径定理进行计算.
14.考点: 垂径定理的应用;勾股定理.
分析: 首先找到EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM是16﹣x,MF=8,然后在直角三角形MOF中利用勾股定理求得OF的长即可.
解答: 解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
设OF=x,则OM=16﹣x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2
即:(16﹣x)2+82=x2
解得:x=10
故答案为:10.
点评: 本题考查了垂径定理及勾股定理的知识,解题的关键是正确的作出辅助线构造直角三角形.
15.【考点】勾股定理的应用;垂径定理的应用
【分析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
解:(1)如图2中,连接B1C1交DD1于H.
∵D1A=D1B1=30
∴D1是的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15,
∴B1C1=30
∴弓臂两端B1,C1的距离为30
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=,
∴r=20,
∴AG=GB2=20,GD1=30﹣20=10,
在Rt△GB2D2中,GD2==10
∴D1D2=10﹣10.
故答案为30,10﹣10,
【点评】本题考查垂径定理的应用、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.
三 、解答题
16.【考点】垂径定理的应用;勾股定理.
【分析】过点O作OM⊥DE于点M,连接OD.
根据垂径定理“垂直于弦的直径平分弦,并且平分弦所对的两条弧”和勾股定理进行计算.
解:过点O作OM⊥DE于点M,连接OD.
∴DM=.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
【点评】综合运用了垂径定理和勾股定理.
17.【考点】垂径定理的应用,勾股定理
【分析】连接OD,由直径AB与弦CD垂直,根据垂径定理得到E为CD的中点,由CD的长求出DE的长,设OD=OA=r寸,则AB=2r寸,OE=(r﹣1)寸,由勾股定理得出方程,解方程求出半径,即可得出直径AB的长.?
解:示意图如图所示, 连接OC
∵AB为⊙O的直径,且CD⊥AB于点E,CD=10,
∴CE=CD=5 .
∵AE=1 ,
设⊙O的半径为r寸, 则OE 为r-1寸
在Rt△CEO中,由勾股定理得
解得r=13,
∴ 直径AB的长为26寸.
18.【考点】作图—复杂作图;勾股定理;垂径定理的应用.
【分析】(1)连结AC、BC,分别作AC和BC的垂直平分线,两垂直平分线的交点为点O,如图1;
(2)连接OA,OC,OC交AB于D,如图2,根据垂径定理的推论,由C为的中点得到OC⊥AB,AD=BD=AB=40,则CD=20,设⊙O的半径为r,在Rt△OAD中利用勾股定理得到r2=(r﹣20)2+402,然后解方程即可.
解:(1)如图1,
点O为所求;
(2)连接OA,OC,OC交AB于D,如图2,
∵C为的中点,
∴OC⊥AB,
∴AD=BD=AB=40,
设⊙O的半径为r,则OA=r,OD=OD﹣CD=r﹣20,
在Rt△OAD中,∵OA2=OD2+AD2,
∴r2=(r﹣20)2+402,解得r=50,
即所在圆的半径是50m.
19.【考点】勾股定理;垂径定理的应用.
【分析】(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
解:(1)作BH⊥PQ于点H.
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°﹣45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2=2=200,
∴台风影响的时间t==5(小时).
故B市受台风影响的时间为5小时.
【点评】本题考查的是直角三角形的性质及垂径定理在实际生活中的运用,解答此题的关键是构造出直角三角形及圆.
同课章节目录
