24.2.2 直线和圆的位置关系(2) 一点就通(知识回顾+夯实基础+提优特训+中考链接+答案)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(2) 一点就通(知识回顾+夯实基础+提优特训+中考链接+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 00:00:00 | ||
图片预览

文档简介
24.2.2直线和圆的位置关系(2)一点就通
【知识回顾】
1.圆的切线的判定定理
经过半径的_____并且_______这条半径的直线是圆的切线.
2.圆的切线的性质定理
圆的切线___________________.
3.判断圆的切线的“三种方法”
(1.)与圆有唯一公共点的直线是圆的切线.
(2.)圆心到直线的距离等于半径,这条直线是圆的切线.
(3.)经过半径的外端点并且垂直于这条半径的直线是圆的切线.
4.常用的辅助线的作法:
①有半径,证垂直;②做锤子,证半径
5.三角形的内切圆
与三角形各边都_____的圆叫做三角形的_____圆.
6.内心
内切圆的圆心是三角形_____________的交点,叫做三角形的_____.
【夯实基础】
1、下列说法正确的是( )
A.过半径的外端的直线是圆的切线
B.到圆心的距离等于半径的直线是圆的切线
C.直角三角形的内心在斜边上
D.三角形有无数个内切圆.
2、如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
3、如图,PA,PB为☉O的切线,A,B分别为切点,∠APB=60°,点P到圆心O的距离OP=2,则☉O的半径为( )
A. B.1 C. D.2
4、如图,从☉O外一点P引圆的两条切线PA,PB,切点分别是A,B,如果∠APB=60°,线段PA=10,那么弦AB的长是( )
A.10 B.12 C.5 D.10
5、如图,AC是☉O的直径,∠ACB=60°,连接AB,过A,B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为 .
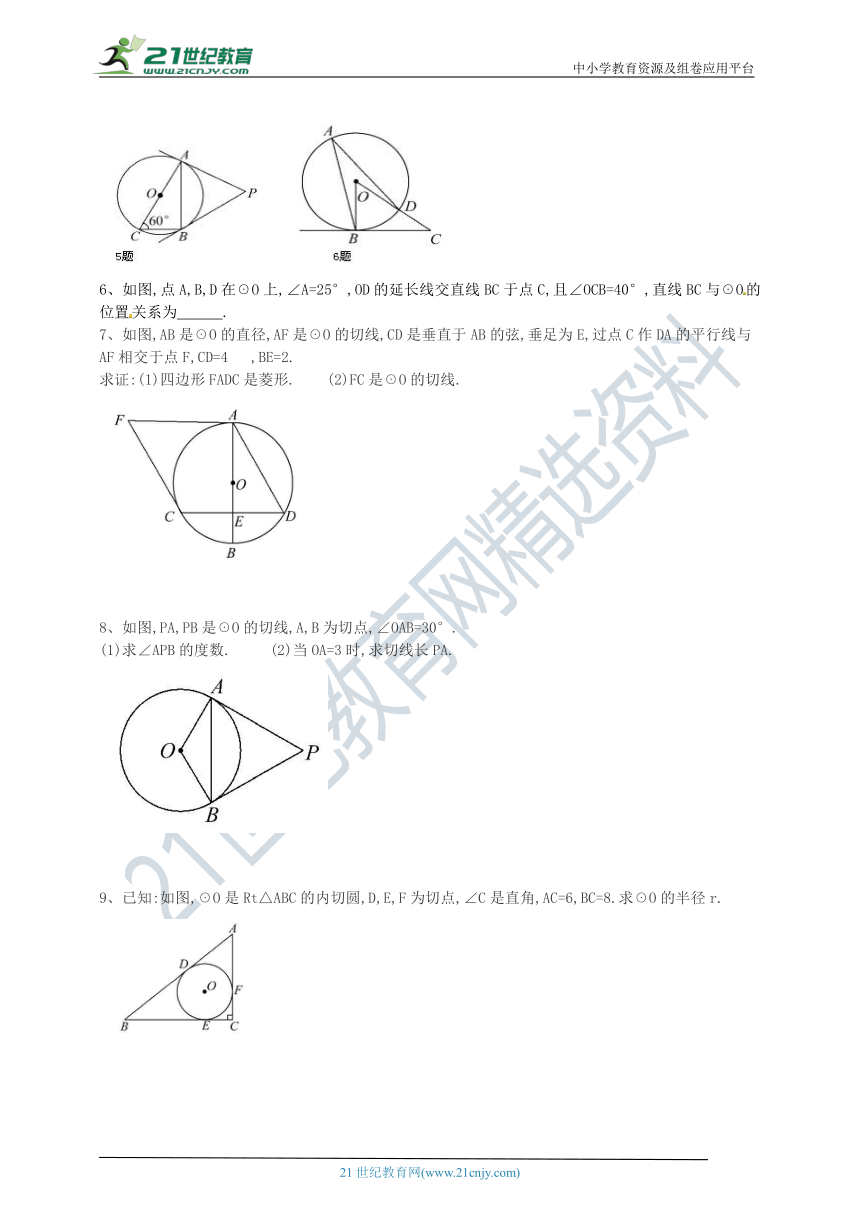
6、如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与☉O的位置关系为 .
7、如图,AB是☉O的直径,AF是☉O的切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=4 ,BE=2.
求证:(1)四边形FADC是菱形. (2)FC是☉O的切线.
8、如图,PA,PB是☉O的切线,A,B为切点,∠OAB=30°.
(1)求∠APB的度数. (2)当OA=3时,求切线长PA.
9、已知:如图,☉O是Rt△ABC的内切圆,D,E,F为切点,∠C是直角,AC=6,BC=8.求☉O的半径r.
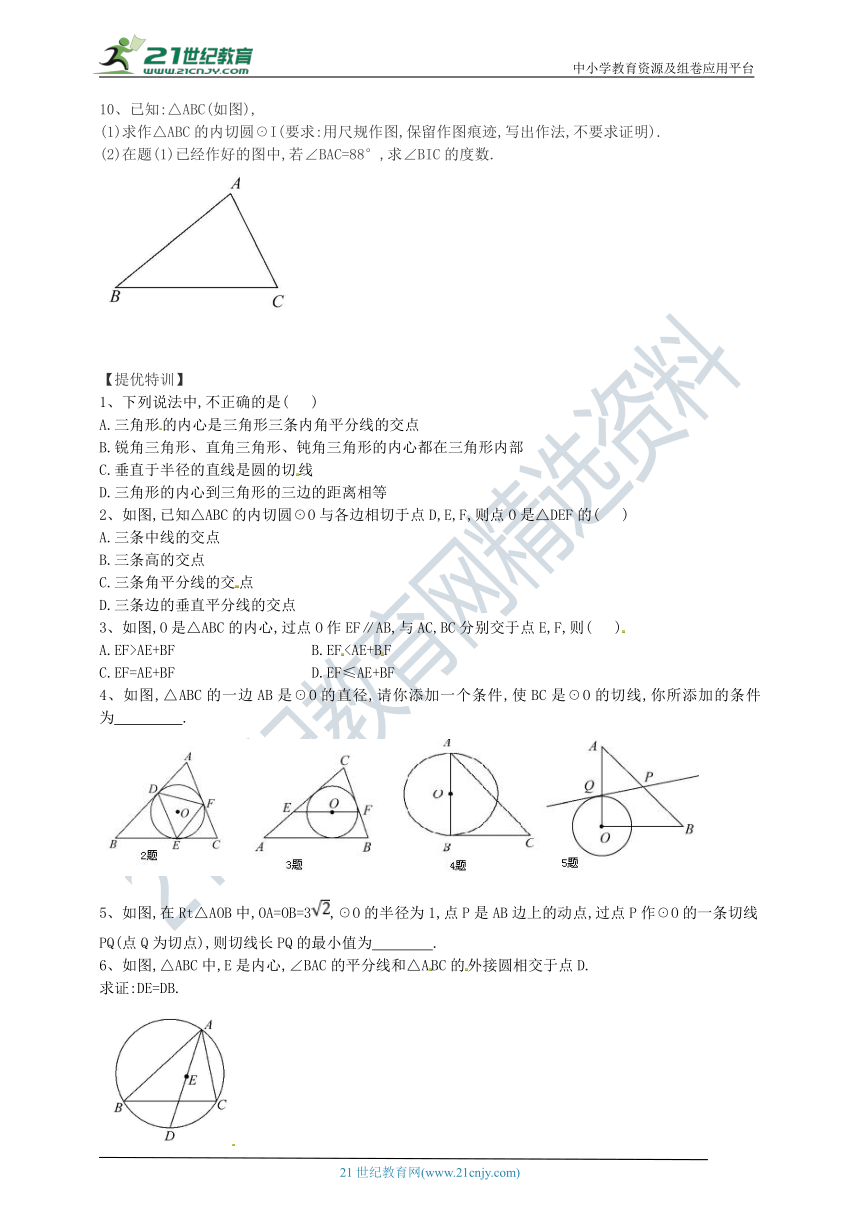
10、已知:△ABC(如图),
(1)求作△ABC的内切圆☉I(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).
(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
【提优特训】
1、下列说法中,不正确的是( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2、如图,已知△ABC的内切圆☉O与各边相切于点D,E,F,则点O是△DEF的( )
A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
3、如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EFC.EF=AE+BF D.EF≤AE+BF
4、如图,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .
5、如图,在Rt△AOB中,OA=OB=3,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(点Q为切点),则切线长PQ的最小值为 .
6、如图,△ABC中,E是内心,∠BAC的平分线和△ABC的外接圆相交于点D.
求证:DE=DB.
7、如图,AB是☉O的直径,C为圆周上一点,BD是☉O的切线,B为切点.
(1)在图(1)中,∠BAC=30°,求∠DBC的度数.
(2)在图(2)中,∠BA1C=40°,求∠DBC的度数.
(3)在图(3)中,∠BA1C=α,求∠DBC的大小.
(4)通过(1),(2),(3)的探究,你发现了什么结论?
【中考链接】
1、(重庆中考)如图,AB是☉O的切线,B为切点,AO与☉O交于点C,若∠BAO=40°,则∠OCB的度数为( )
A.40° B.50° C.65° D.75°
2、(滨州中考)如图,在△ABC中,AB=AC,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
求证:直线EF是☉O的切线.
3、(牡丹江中考)如图,点C是☉O的直径AB延长线上的一点,且有BO=BD=BC.
(1)求证:CD是☉O的切线. (2)若半径OB=2,求AD的长.
【参考答案】
【夯实基础答案】
1.B 2. D 3. B 4. A 5.3 6.相切
7.(1)连接OC,依题意知:AF⊥AB,又CD⊥AB,∴AF∥CD,
又CF∥AD,∴四边形FADC是平行四边形,
由垂径定理得:CE=ED= CD=2 ,
设☉O的半径为R,则OC=R,OE=OB-BE=R-2,
在△ECO中,由勾股定理得:
R2=(R-2)2+(2)2,解得:R=4,
∴AD=
∴AD=CD,
因此平行四边形FADC是菱形.
(2)连接OF,由(1)得:FC=FA,又OC=OA,FO=FO,∴△FCO≌△FAO,∴∠FCO=∠FAO=90°,
因此FC是☉O的切线.
9.连接OE,OF,由勾股定理得,
AB=, S⊿ABC=×6×8=24
∵☉O是Rt△ABC的内切圆,∴CE=CF,AD=AF,BD=BE,
设CE的长为x,则BE可表示为8-x,AF可表示为6-x.
∴AB=AD+BD=AF+BE=6-x+8-x=14-2x=10,解得x=2,即CF=CE=2.
∵☉O是Rt△ABC的内切圆,E,F为切点,∴∠OFC=∠OEC=90°,
又∠C=90°.∴四边形OECF为矩形,∴CF等于Rt△ABC的内切圆的半径,即r=2.
∴四边形OECF为矩形,∴CF等于Rt△ABC的内切圆的半径,即r=2
10.(1)图略
(2)∵∠BAC=88°,∴∠ABC+∠ACB=180°-88°=92°,
∴∠IBC+∠ICB= (∠ABC+∠ACB)= ×92°=46°,
∴∠BIC=180°-46°=134°.
【提优特训答案】
1.C 2. D 3. C 4.∠ABC=90°
5.2
提示:连接OP,OQ.
∵PQ是☉O的切线,
∴OQ⊥PQ.
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短.
∵在Rt△AOB中,
OA=OB=3,
∴AB2=OA2+OB2=36,即AB=6.
∵S△AOB=OA·OB=OP·AB,∴OP=3,
由PQ2=OP2-OQ2,OQ=1,
∴PQ==2.
6.证明:连接EB,DB.
∵E是△ABC的内心,∴∠EBC=∠ABE,∠BAD=∠CAD.
∵∠CAD=∠CBD,∴∠BAD=∠CBD.
又∵∠BED=∠BAD+∠ABE,
∠DBE=∠EBC+∠CBD,
∴∠BED=∠DBE,∴DE=DB.
7.(1)∵AB是☉O的直径,∴∠ACB=90°.∵∠BAC=30°,∴∠ABC=60°.
∵BD是☉O的切线,∴∠ABD=90°,∴∠DBC=30°.
(2)连接AC,则∠BAC=∠BA1C=40°,根据(1)可得∠DBC=40°.
(3)连接AC,则∠BAC=∠BA1C=α,根据(1)可得∠DBC=α.
(4)圆的切线与弦所成的角等于它们所夹的弧所对的圆周角.
【中考链接答案】
1.C
2.连接OE,
∵OB=OE,∴∠B=∠OEB.∵AB=AC,∴∠B=∠C.
∴∠OEB=∠C.∴OE∥AC.∵EF⊥AC,∴OE⊥EF.
∴直线EF是☉O的切线.
3.(1)连接OD,如图,
则有BO=BD=BC=DO,
∴∠C=∠CDB,∠DOB=∠BDO.
又∵∠C+∠CDB+∠DOB+∠BDO=180°,
∴∠CDB+∠BDO=90°,
即∠CDO=90°,
∴CD是☉O的切线.
(2)∵OB=2,∴BD=OB=2,AB=4.
∵AB是直径,∴∠ADB=90°,∴AD=2.
【知识回顾】
1.圆的切线的判定定理
经过半径的_____并且_______这条半径的直线是圆的切线.
2.圆的切线的性质定理
圆的切线___________________.
3.判断圆的切线的“三种方法”
(1.)与圆有唯一公共点的直线是圆的切线.
(2.)圆心到直线的距离等于半径,这条直线是圆的切线.
(3.)经过半径的外端点并且垂直于这条半径的直线是圆的切线.
4.常用的辅助线的作法:
①有半径,证垂直;②做锤子,证半径
5.三角形的内切圆
与三角形各边都_____的圆叫做三角形的_____圆.
6.内心
内切圆的圆心是三角形_____________的交点,叫做三角形的_____.
【夯实基础】
1、下列说法正确的是( )
A.过半径的外端的直线是圆的切线
B.到圆心的距离等于半径的直线是圆的切线
C.直角三角形的内心在斜边上
D.三角形有无数个内切圆.
2、如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
3、如图,PA,PB为☉O的切线,A,B分别为切点,∠APB=60°,点P到圆心O的距离OP=2,则☉O的半径为( )
A. B.1 C. D.2
4、如图,从☉O外一点P引圆的两条切线PA,PB,切点分别是A,B,如果∠APB=60°,线段PA=10,那么弦AB的长是( )
A.10 B.12 C.5 D.10
5、如图,AC是☉O的直径,∠ACB=60°,连接AB,过A,B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为 .
6、如图,点A,B,D在☉O上,∠A=25°,OD的延长线交直线BC于点C,且∠OCB=40°,直线BC与☉O的位置关系为 .
7、如图,AB是☉O的直径,AF是☉O的切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=4 ,BE=2.
求证:(1)四边形FADC是菱形. (2)FC是☉O的切线.
8、如图,PA,PB是☉O的切线,A,B为切点,∠OAB=30°.
(1)求∠APB的度数. (2)当OA=3时,求切线长PA.
9、已知:如图,☉O是Rt△ABC的内切圆,D,E,F为切点,∠C是直角,AC=6,BC=8.求☉O的半径r.
10、已知:△ABC(如图),
(1)求作△ABC的内切圆☉I(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).
(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
【提优特训】
1、下列说法中,不正确的是( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2、如图,已知△ABC的内切圆☉O与各边相切于点D,E,F,则点O是△DEF的( )
A.三条中线的交点
B.三条高的交点
C.三条角平分线的交点
D.三条边的垂直平分线的交点
3、如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( )
A.EF>AE+BF B.EF
4、如图,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .
5、如图,在Rt△AOB中,OA=OB=3,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(点Q为切点),则切线长PQ的最小值为 .
6、如图,△ABC中,E是内心,∠BAC的平分线和△ABC的外接圆相交于点D.
求证:DE=DB.
7、如图,AB是☉O的直径,C为圆周上一点,BD是☉O的切线,B为切点.
(1)在图(1)中,∠BAC=30°,求∠DBC的度数.
(2)在图(2)中,∠BA1C=40°,求∠DBC的度数.
(3)在图(3)中,∠BA1C=α,求∠DBC的大小.
(4)通过(1),(2),(3)的探究,你发现了什么结论?
【中考链接】
1、(重庆中考)如图,AB是☉O的切线,B为切点,AO与☉O交于点C,若∠BAO=40°,则∠OCB的度数为( )
A.40° B.50° C.65° D.75°
2、(滨州中考)如图,在△ABC中,AB=AC,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
求证:直线EF是☉O的切线.
3、(牡丹江中考)如图,点C是☉O的直径AB延长线上的一点,且有BO=BD=BC.
(1)求证:CD是☉O的切线. (2)若半径OB=2,求AD的长.
【参考答案】
【夯实基础答案】
1.B 2. D 3. B 4. A 5.3 6.相切
7.(1)连接OC,依题意知:AF⊥AB,又CD⊥AB,∴AF∥CD,
又CF∥AD,∴四边形FADC是平行四边形,
由垂径定理得:CE=ED= CD=2 ,
设☉O的半径为R,则OC=R,OE=OB-BE=R-2,
在△ECO中,由勾股定理得:
R2=(R-2)2+(2)2,解得:R=4,
∴AD=
∴AD=CD,
因此平行四边形FADC是菱形.
(2)连接OF,由(1)得:FC=FA,又OC=OA,FO=FO,∴△FCO≌△FAO,∴∠FCO=∠FAO=90°,
因此FC是☉O的切线.
9.连接OE,OF,由勾股定理得,
AB=, S⊿ABC=×6×8=24
∵☉O是Rt△ABC的内切圆,∴CE=CF,AD=AF,BD=BE,
设CE的长为x,则BE可表示为8-x,AF可表示为6-x.
∴AB=AD+BD=AF+BE=6-x+8-x=14-2x=10,解得x=2,即CF=CE=2.
∵☉O是Rt△ABC的内切圆,E,F为切点,∴∠OFC=∠OEC=90°,
又∠C=90°.∴四边形OECF为矩形,∴CF等于Rt△ABC的内切圆的半径,即r=2.
∴四边形OECF为矩形,∴CF等于Rt△ABC的内切圆的半径,即r=2
10.(1)图略
(2)∵∠BAC=88°,∴∠ABC+∠ACB=180°-88°=92°,
∴∠IBC+∠ICB= (∠ABC+∠ACB)= ×92°=46°,
∴∠BIC=180°-46°=134°.
【提优特训答案】
1.C 2. D 3. C 4.∠ABC=90°
5.2
提示:连接OP,OQ.
∵PQ是☉O的切线,
∴OQ⊥PQ.
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短.
∵在Rt△AOB中,
OA=OB=3,
∴AB2=OA2+OB2=36,即AB=6.
∵S△AOB=OA·OB=OP·AB,∴OP=3,
由PQ2=OP2-OQ2,OQ=1,
∴PQ==2.
6.证明:连接EB,DB.
∵E是△ABC的内心,∴∠EBC=∠ABE,∠BAD=∠CAD.
∵∠CAD=∠CBD,∴∠BAD=∠CBD.
又∵∠BED=∠BAD+∠ABE,
∠DBE=∠EBC+∠CBD,
∴∠BED=∠DBE,∴DE=DB.
7.(1)∵AB是☉O的直径,∴∠ACB=90°.∵∠BAC=30°,∴∠ABC=60°.
∵BD是☉O的切线,∴∠ABD=90°,∴∠DBC=30°.
(2)连接AC,则∠BAC=∠BA1C=40°,根据(1)可得∠DBC=40°.
(3)连接AC,则∠BAC=∠BA1C=α,根据(1)可得∠DBC=α.
(4)圆的切线与弦所成的角等于它们所夹的弧所对的圆周角.
【中考链接答案】
1.C
2.连接OE,
∵OB=OE,∴∠B=∠OEB.∵AB=AC,∴∠B=∠C.
∴∠OEB=∠C.∴OE∥AC.∵EF⊥AC,∴OE⊥EF.
∴直线EF是☉O的切线.
3.(1)连接OD,如图,
则有BO=BD=BC=DO,
∴∠C=∠CDB,∠DOB=∠BDO.
又∵∠C+∠CDB+∠DOB+∠BDO=180°,
∴∠CDB+∠BDO=90°,
即∠CDO=90°,
∴CD是☉O的切线.
(2)∵OB=2,∴BD=OB=2,AB=4.
∵AB是直径,∴∠ADB=90°,∴AD=2.
同课章节目录
