初中数学沪科版九年级上册第23章解直角三角形检测卷含答案
文档属性
| 名称 | 初中数学沪科版九年级上册第23章解直角三角形检测卷含答案 | 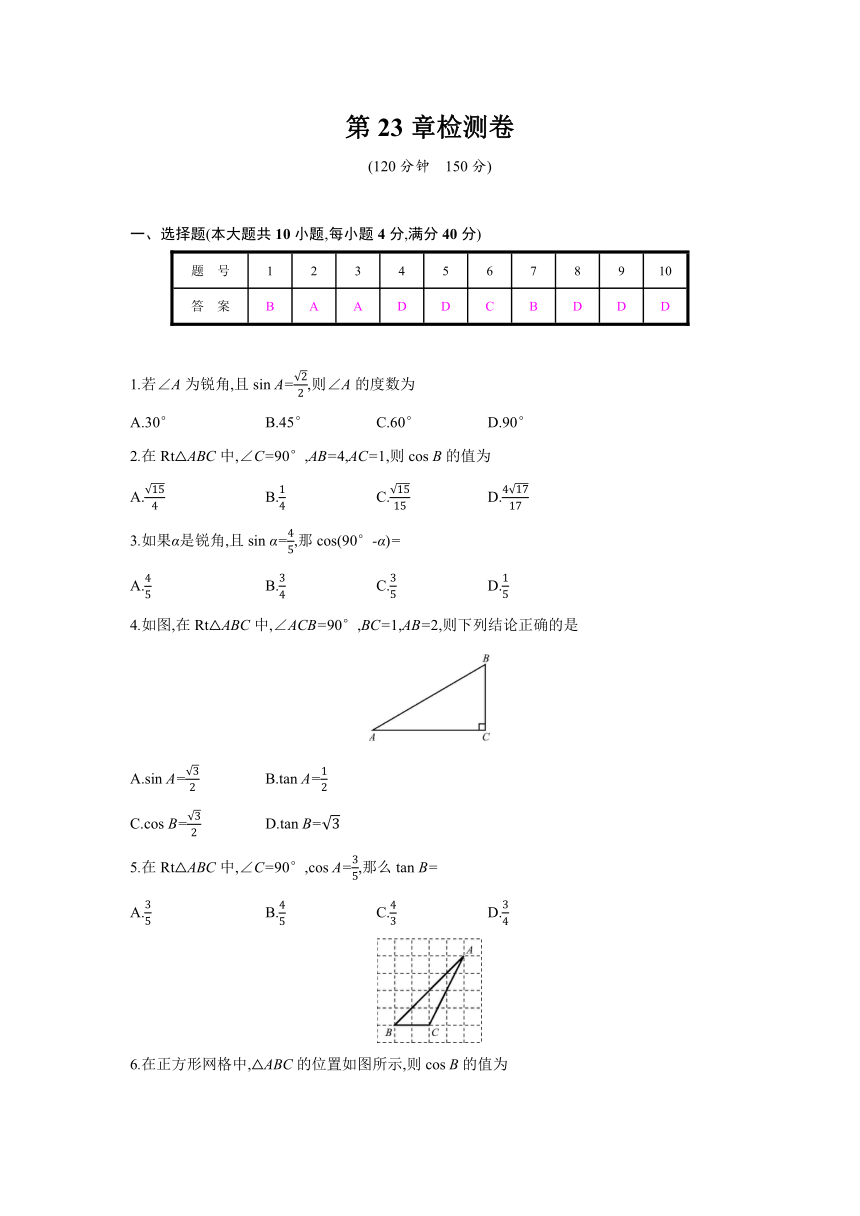 | |
| 格式 | zip | ||
| 文件大小 | 219.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 14:53:12 | ||
图片预览



文档简介
第23章检测卷
(120分钟 150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 B A A D D C B D D D
1.若∠A为锐角,且sin A=,则∠A的度数为
A.30° B.45° C.60° D.90°
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cos B的值为
A. B. C. D.
3.如果α是锐角,且sin α=,那cos(90°-α)=
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是
A.sin A= B.tan A=
C.cos B= D.tan B=
5.在Rt△ABC中,∠C=90°,cos A=,那么tan B=
A. B. C. D.
6.在正方形网格中,△ABC的位置如图所示,则cos B的值为
A. B.
C. D.
7.若一个等腰三角形腰长为4,面积是4,则这个等腰三角形顶角的度数为
A.30° B.30°或150°
C.60° D.60°或120°
8.已知sin α>cos α,那么锐角α的取值范围是
A.30°<α<45° B.0°<α<45°
C.45°<α<60° D.45°<α<90°
9.在Rt△ABC中,∠C=90°,下列式子中不一定成立的是
A.tan A= B.sin2A+sin2B=1
C.sin2A+cos2A=1 D.sin A=sin B
10.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船.那么救援船航行的速度为
A.10海里/时 B.30海里/时
C.20海里/时 D.30海里/时
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若cos A>,则锐角A的取值范围是 0°
12.计算:1+tan 60°+= 2+ .?
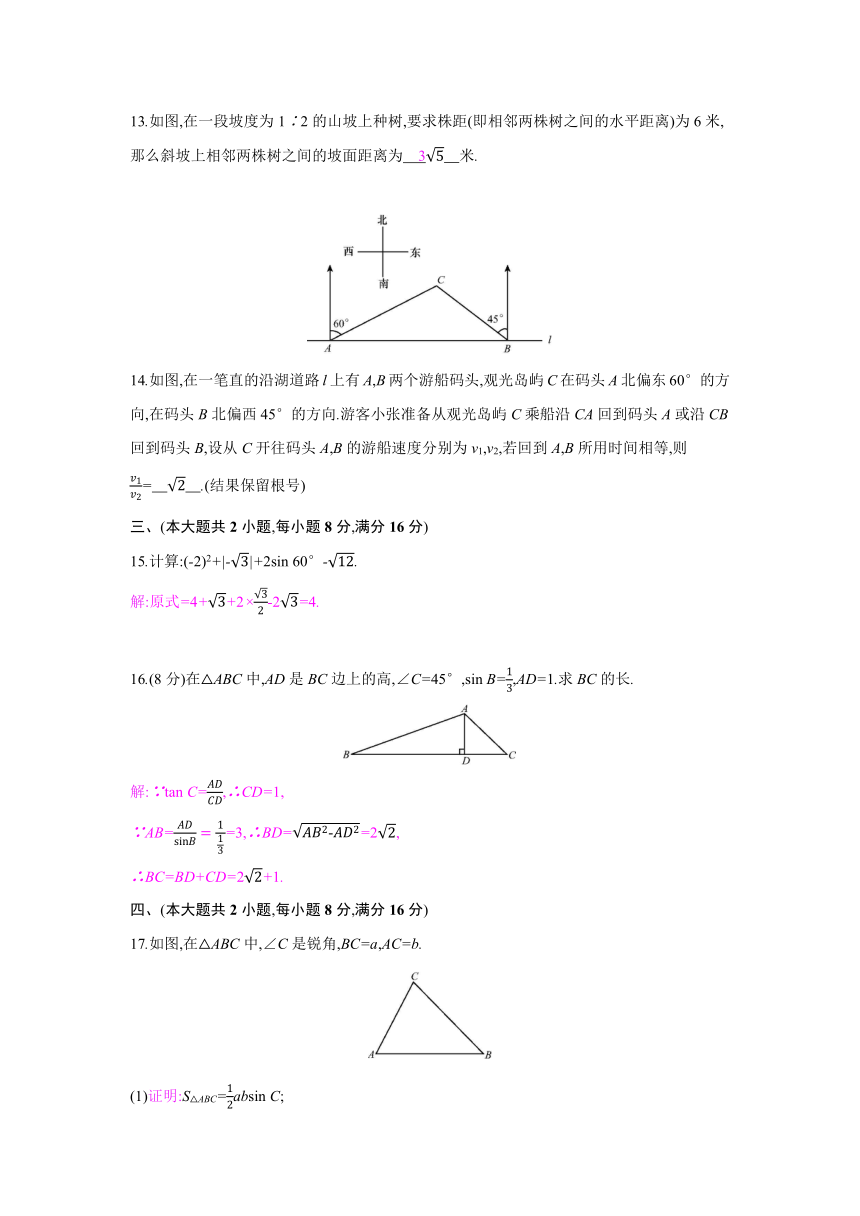
13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为 3 米.?
14.如图,在一笔直的沿湖道路l上有A,B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏西45°的方向.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设从C开往码头A,B的游船速度分别为v1,v2,若回到A,B所用时间相等,则=? .(结果保留根号)?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(-2)2+|-|+2sin 60°-.
解:原式=4++2×-2=4.
16.(8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1.求BC的长.
解:∵tan C=,∴CD=1,
∵AB==3,∴BD==2,
∴BC=BD+CD=2+1.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在△ABC中,∠C是锐角,BC=a,AC=b.
(1)证明:S△ABC=absin C;
(2)若△ABC是等边三角形,边长为4,求△ABC的面积.
解:(1)过点A作AD⊥BC于点D,
在Rt△ACD中,AD=AC·sin C,
∴S△ABC=BC·AD=absin C.
(2)由(1)知S△ABC=×4×4×sin 60°=×4×4×=4.
18.一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,求点B的坐标.
解:过B点作BE⊥x轴于点E,
由∠BEC=∠COA,∠EBC=∠OCA,∴△EBC∽△OCA,
∴,
在Rt△ACO中,AC=,
在Rt△ABC中,∠CBA=30°,∴tan ∠CBA=,
∴BC=,
∴,解得BE=3,EC=,
∴EO=EC+CO=+3,
∴点B的坐标为(-3-,3).
五、(本大题共2小题,每小题10分,满分20分)
19.如图,某居民小区内A,B两楼之间的距离MN=30米,两楼的高都是20米,A楼在B楼正南方向,B楼窗户朝南.B楼内一楼住户的窗台离小区地面的距离DN=2米,窗户高CD=1.8米.当正午时刻太阳光线与地面成30°角时,A楼的影子是否影响B楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:≈1.414,≈1.732,≈2.236)
解:如图,设光线FE影响到B楼的E处.
作EG⊥FM于点G,由题知四边形GMNE是矩形,
所以EG=MN=30米,∠FEG=30°,
在Rt△EGF中,FG=EG×tan 30°=30×=10≈17.32(米),
则EN=MG=FM-GF=20-17.32=2.68(米),
因为DN=2米,CD=1.8米,
所以ED=2.68-2=0.68(米),
即A楼影子影响到B楼的一楼住户采光,挡住该住户窗户0.68米.
20.一艘海轮上午九点于A处观察到在其北偏东30°的方向上有一灯塔S,随后海轮沿北偏东70°的方向航行,于十一点到达点B处,测得此时灯塔S在其北偏西70°的方向上,若灯塔S距离点A处20海里,求海轮的航行速度.(结果精确到1海里)(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
解:由题意知∠SAB=70°-30°=40°,∠SBA=(90°-70°)+(90°-70°)=40°,∴∠SAB=∠SBA,∴AS=BS=20.
过点S作SC⊥AB于点C,则AC=BC.
在Rt△ACS中,AS=20,∠SAC=40°,∵cos 40°=,
∴AC≈20×0.77=15.4,∴AB=2AC≈30.8,
∴海轮的速度约为30.8÷(11-9)=30.8÷2=15.4≈15(海里/小时).
六、(本题满分12分)
21.“兰州中山桥”位于兰州滨河路中段白塔山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥”之美誉.它像一部史诗,记载着兰州古往今来历史的变迁.桥上飞架了五座等高的弧形钢架拱桥.
小芸和小刚分别在桥面上的A,B两处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离,其中AB=20 m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁桥顶部C处到桥面的距离.(结果精确到0.1 m)(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73,sin 43°≈0.68,cos 43°≈0.73,tan 43°≈0.93)
过点C做CD⊥AB于点D,设CD长为x.
根据题意,在Rt△CDB中,=tan 43°≈0.93,则BD=;
在Rt△CDA中,=tan 36°≈0.73,则AD=.
又AB=20 m,∴=20,
∴x=20÷=8.179≈8.2 m
所以弧形钢架拱梁桥顶部C处到桥面的距离为8.2 m.
七、(本题满分12分)
22.一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如图2的技术要求.试求出改造后坡面的坡度是多少?
解:由图1可知BE⊥DC,BE=30 m,sin α=0.6,
在Rt△BEC中,∵sin α=,
∴BC==50(m),
在Rt△BEC中,由勾股定理得EC=40 m.
在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,
则梯形ABCD的面积=梯形A1B1C1D1的面积,
∴×(20+60)×30=×20×(20+20+E1C1)
解得E1C1=80 m,
∴改建后的坡度i=B1E1∶E1C1=20∶80=1∶4.
八、(本题满分14分)
23.如图,某海滨浴场的海岸线可以看作直线,1号救生员在岸边的点A处看到海中的点B处有人求救,便立即向前跑300米到离点B处最近的点D处,再跳入海中沿直线游到点B处救助.若救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,且∠BAD=45°.
(1)请问1号救生员到达点B处的时间是多少?
(2)若2号救生员先从点A跑到点C处,再跳入海中沿直线游到点B处救助,且∠BCD=60°,请问1号救生员与2号救生员谁先到达点B处?(参考数据:≈1.414,≈1.732)
解:(1)在Rt△ABD中,∠BAD=45°,∴BD=AD=300米,由题意得t1==50,t2==150,
∴t=t1+t2=200秒,即1号救生员到达点B处的时间是200秒.
(2)在Rt△BCD中,∠BCD=60°,∴CD==100米,BC==200米,
∴AC=(300-100)米,
∴T==50+≈194(秒),
∵194<200,∴2号救生员先到达.
(120分钟 150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 B A A D D C B D D D
1.若∠A为锐角,且sin A=,则∠A的度数为
A.30° B.45° C.60° D.90°
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cos B的值为
A. B. C. D.
3.如果α是锐角,且sin α=,那cos(90°-α)=
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是
A.sin A= B.tan A=
C.cos B= D.tan B=
5.在Rt△ABC中,∠C=90°,cos A=,那么tan B=
A. B. C. D.
6.在正方形网格中,△ABC的位置如图所示,则cos B的值为
A. B.
C. D.
7.若一个等腰三角形腰长为4,面积是4,则这个等腰三角形顶角的度数为
A.30° B.30°或150°
C.60° D.60°或120°
8.已知sin α>cos α,那么锐角α的取值范围是
A.30°<α<45° B.0°<α<45°
C.45°<α<60° D.45°<α<90°
9.在Rt△ABC中,∠C=90°,下列式子中不一定成立的是
A.tan A= B.sin2A+sin2B=1
C.sin2A+cos2A=1 D.sin A=sin B
10.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船.那么救援船航行的速度为
A.10海里/时 B.30海里/时
C.20海里/时 D.30海里/时
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若cos A>,则锐角A的取值范围是 0°
12.计算:1+tan 60°+= 2+ .?
13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为 3 米.?
14.如图,在一笔直的沿湖道路l上有A,B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏西45°的方向.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设从C开往码头A,B的游船速度分别为v1,v2,若回到A,B所用时间相等,则=? .(结果保留根号)?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(-2)2+|-|+2sin 60°-.
解:原式=4++2×-2=4.
16.(8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1.求BC的长.
解:∵tan C=,∴CD=1,
∵AB==3,∴BD==2,
∴BC=BD+CD=2+1.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在△ABC中,∠C是锐角,BC=a,AC=b.
(1)证明:S△ABC=absin C;
(2)若△ABC是等边三角形,边长为4,求△ABC的面积.
解:(1)过点A作AD⊥BC于点D,
在Rt△ACD中,AD=AC·sin C,
∴S△ABC=BC·AD=absin C.
(2)由(1)知S△ABC=×4×4×sin 60°=×4×4×=4.
18.一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,求点B的坐标.
解:过B点作BE⊥x轴于点E,
由∠BEC=∠COA,∠EBC=∠OCA,∴△EBC∽△OCA,
∴,
在Rt△ACO中,AC=,
在Rt△ABC中,∠CBA=30°,∴tan ∠CBA=,
∴BC=,
∴,解得BE=3,EC=,
∴EO=EC+CO=+3,
∴点B的坐标为(-3-,3).
五、(本大题共2小题,每小题10分,满分20分)
19.如图,某居民小区内A,B两楼之间的距离MN=30米,两楼的高都是20米,A楼在B楼正南方向,B楼窗户朝南.B楼内一楼住户的窗台离小区地面的距离DN=2米,窗户高CD=1.8米.当正午时刻太阳光线与地面成30°角时,A楼的影子是否影响B楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:≈1.414,≈1.732,≈2.236)
解:如图,设光线FE影响到B楼的E处.
作EG⊥FM于点G,由题知四边形GMNE是矩形,
所以EG=MN=30米,∠FEG=30°,
在Rt△EGF中,FG=EG×tan 30°=30×=10≈17.32(米),
则EN=MG=FM-GF=20-17.32=2.68(米),
因为DN=2米,CD=1.8米,
所以ED=2.68-2=0.68(米),
即A楼影子影响到B楼的一楼住户采光,挡住该住户窗户0.68米.
20.一艘海轮上午九点于A处观察到在其北偏东30°的方向上有一灯塔S,随后海轮沿北偏东70°的方向航行,于十一点到达点B处,测得此时灯塔S在其北偏西70°的方向上,若灯塔S距离点A处20海里,求海轮的航行速度.(结果精确到1海里)(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
解:由题意知∠SAB=70°-30°=40°,∠SBA=(90°-70°)+(90°-70°)=40°,∴∠SAB=∠SBA,∴AS=BS=20.
过点S作SC⊥AB于点C,则AC=BC.
在Rt△ACS中,AS=20,∠SAC=40°,∵cos 40°=,
∴AC≈20×0.77=15.4,∴AB=2AC≈30.8,
∴海轮的速度约为30.8÷(11-9)=30.8÷2=15.4≈15(海里/小时).
六、(本题满分12分)
21.“兰州中山桥”位于兰州滨河路中段白塔山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥”之美誉.它像一部史诗,记载着兰州古往今来历史的变迁.桥上飞架了五座等高的弧形钢架拱桥.
小芸和小刚分别在桥面上的A,B两处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离,其中AB=20 m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁桥顶部C处到桥面的距离.(结果精确到0.1 m)(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73,sin 43°≈0.68,cos 43°≈0.73,tan 43°≈0.93)
过点C做CD⊥AB于点D,设CD长为x.
根据题意,在Rt△CDB中,=tan 43°≈0.93,则BD=;
在Rt△CDA中,=tan 36°≈0.73,则AD=.
又AB=20 m,∴=20,
∴x=20÷=8.179≈8.2 m
所以弧形钢架拱梁桥顶部C处到桥面的距离为8.2 m.
七、(本题满分12分)
22.一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如图2的技术要求.试求出改造后坡面的坡度是多少?
解:由图1可知BE⊥DC,BE=30 m,sin α=0.6,
在Rt△BEC中,∵sin α=,
∴BC==50(m),
在Rt△BEC中,由勾股定理得EC=40 m.
在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,
则梯形ABCD的面积=梯形A1B1C1D1的面积,
∴×(20+60)×30=×20×(20+20+E1C1)
解得E1C1=80 m,
∴改建后的坡度i=B1E1∶E1C1=20∶80=1∶4.
八、(本题满分14分)
23.如图,某海滨浴场的海岸线可以看作直线,1号救生员在岸边的点A处看到海中的点B处有人求救,便立即向前跑300米到离点B处最近的点D处,再跳入海中沿直线游到点B处救助.若救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,且∠BAD=45°.
(1)请问1号救生员到达点B处的时间是多少?
(2)若2号救生员先从点A跑到点C处,再跳入海中沿直线游到点B处救助,且∠BCD=60°,请问1号救生员与2号救生员谁先到达点B处?(参考数据:≈1.414,≈1.732)
解:(1)在Rt△ABD中,∠BAD=45°,∴BD=AD=300米,由题意得t1==50,t2==150,
∴t=t1+t2=200秒,即1号救生员到达点B处的时间是200秒.
(2)在Rt△BCD中,∠BCD=60°,∴CD==100米,BC==200米,
∴AC=(300-100)米,
∴T==50+≈194(秒),
∵194<200,∴2号救生员先到达.
