八年级数学第3章《勾股定理》同步提高测试
文档属性
| 名称 | 八年级数学第3章《勾股定理》同步提高测试 |
|
|
| 格式 | zip | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 00:00:00 | ||
图片预览


文档简介
八年级数学第3章《勾股定理》同步提高测试
一、选择题:
1、下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 ;B.2,3,4; C.4,6,7; D.5,11,12;
2、直角三角形有一条直角边长为6,另两条边长是连续偶数,则该三角形的周长为( )
A. 20 B. 22 C. 24 D. 26
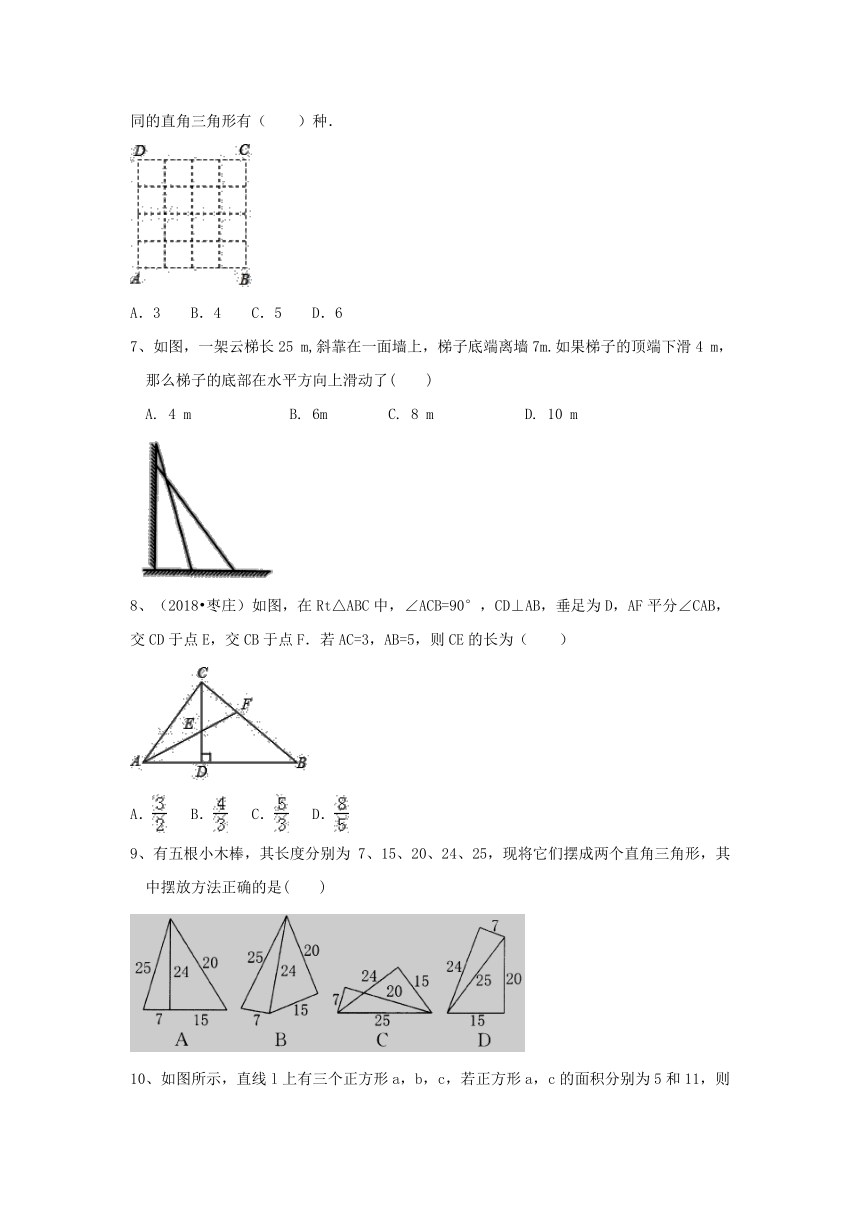
3、如图,每个小正方形的边长为1,若是小正方形的顶点,则的度数为( )
A. 90? B. 60? C. 45? D. 30?
4、等腰直角三角尺与直尺按如图位置摆放,且三角尺在直角顶点在直尺的一边上.若∠1=35°,则∠2的度数是( )
A.95° B.100° C.105° D.110°
5、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的面积为………( )
A.16㎝ B.15㎝ ;C.14㎝ ; D.9㎝;
6、在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
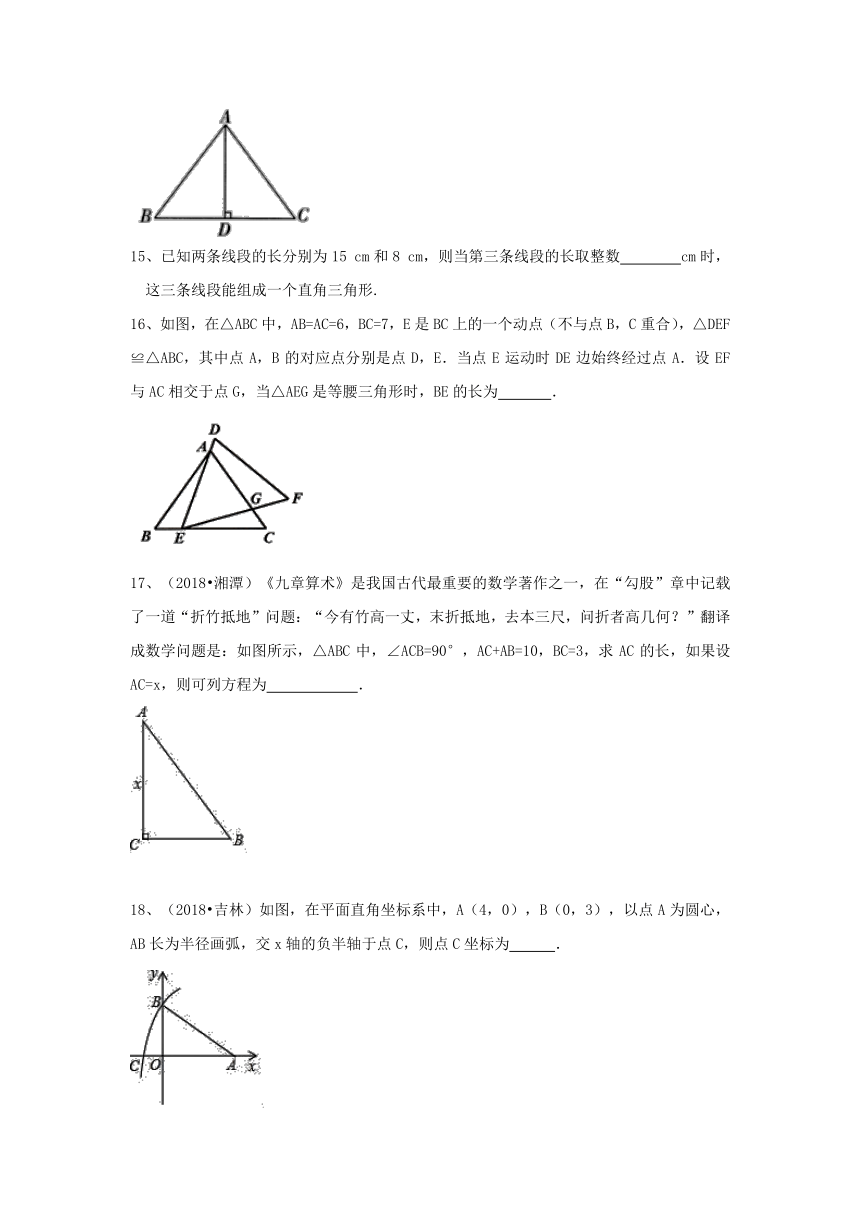
7、如图,一架云梯长25 m,斜靠在一面墙上,梯子底端离墙7m.如果梯子的顶端下滑4 m,那么梯子的底部在水平方向上滑动了( )
A. 4 m B. 6m C. 8 m D. 10 m
8、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
9、有五根小木棒,其长度分别为7、15、20、24、25,现将它们摆成两个直角三角形,其中摆放方法正确的是( )
10、如图所示,直线l上有三个正方形a,b,c,若正方形a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
11、(2018?温州)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A.20 B.24 C. D.
12、如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9中,正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
二、填空题:
13、直角三角形两直角边长分别为3和4,则它斜边上的高为
14、如图,在中,cm,cm,于点,则
cm.
15、已知两条线段的长分别为15 cm和8 cm,则当第三条线段的长取整数 cm时,这三条线段能组成一个直角三角形.
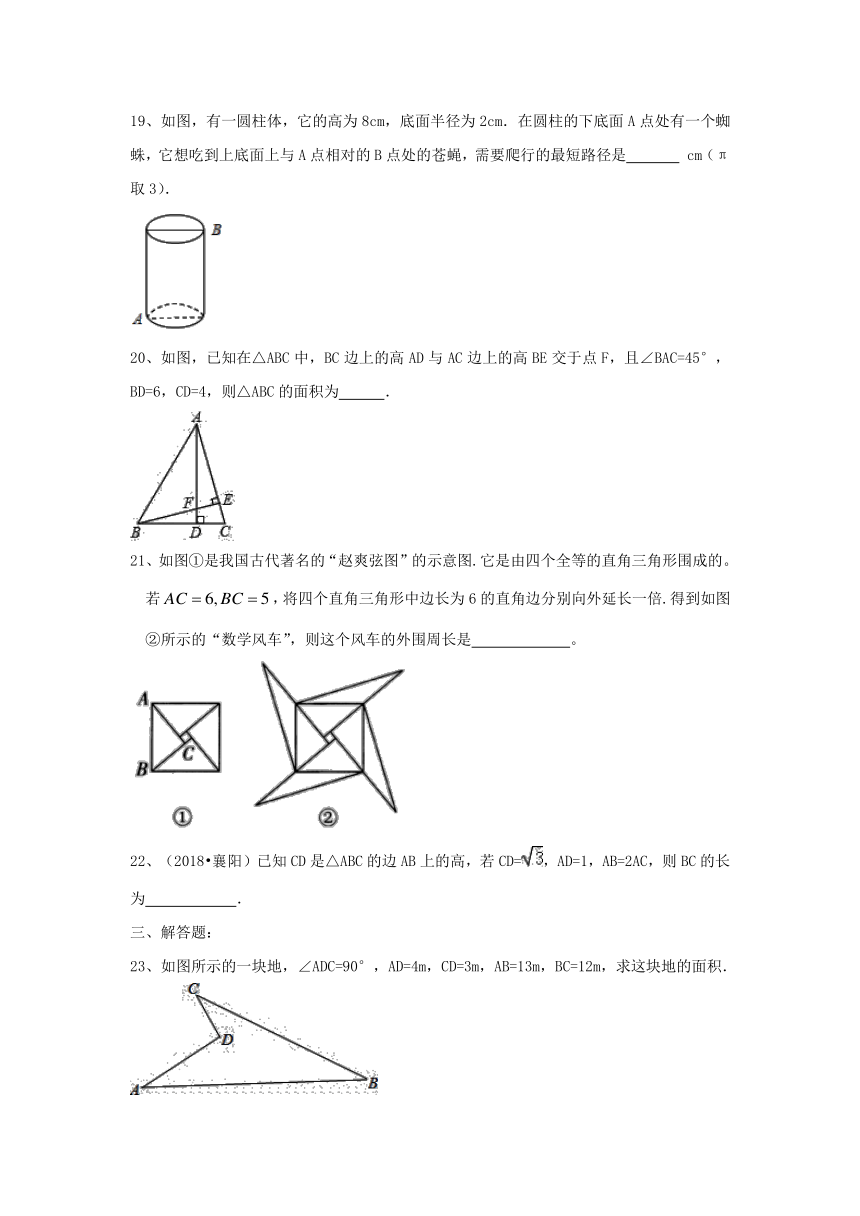
16、如图,在△ABC中,AB=AC=6,BC=7,E是BC上的一个动点(不与点B,C重合),△DEF≌△ABC,其中点A,B的对应点分别是点D,E.当点E运动时DE边始终经过点A.设EF与AC相交于点G,当△AEG是等腰三角形时,BE的长为 .
17、(2018?湘潭)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
18、(2018?吉林)如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 .
19、如图,有一圆柱体,它的高为8cm,底面半径为2cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm(π取3).
20、如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为 .
21、如图①是我国古代著名的“赵爽弦图”的示意图.它是由四个全等的直角三角形围成的。若,将四个直角三角形中边长为6的直角边分别向外延长一倍.得到如图②所示的“数学风车”,则这个风车的外围周长是 。
22、(2018?襄阳)已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
三、解答题:
23、如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.
24、某路段限速标志规定:小汽车在此路段上行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30米的C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离50米.
(1)求BC的长;
(2)这辆小汽车超速了吗?
25、为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?
26、如图所示,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再转向北走到4.5 km处往东一拐,仅走0.5 km就找到了宝藏.则登陆点A与宝藏埋藏点B之间的距离是多少?
27、(2018?杭州)如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.
(1)若∠A=28°,求∠ACD的度数.
(2)设BC=a,AC=b.
①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.
②若AD=EC,求的值.
一、选择题:
1、A
2、C
3、C
4、B
5、C
6、A
7、C
8、A
9、D
10、C
11、B
12、B
二、填空题:
13、12/5
14、8
15、17
16、1或13/7
17、x2+32=(10﹣x)2
18、(﹣1,0)
19、10
20、60
21、76
22、2或2
三、解答题:
23、24m2
24、解:(1)∵AC=30米 AB=50米
又∵三角形ABC为直角三角形,根据勾股定理:
AC2+BC2=AB2
∴BC=40米
(2)汽车的速度为40米÷2秒=20米/秒=72千米/时
∴这辆小汽车超速了
25、解:(1)连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
则S四边形ABCD=S△BAD+S△DBC=?AD?AB+DB?BC=×4×3+×12×5=36;
(2)所以需费用36×200=7200(元).
26、解:如图,过点B作BC⊥AD于点C,
则AC=4-2+0.5=2.5(km),BC=4.5+1.5=6(km).
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=2.52+62=6.52,∴AB=6.5(km).
答:登陆点A与宝藏埋藏点B之间的距离是6.5 km.
27、解:(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°﹣∠BCD=31°;
(2)①由勾股定理得,AB==,
∴AD=﹣a,
解方程x2+2ax﹣b2=0得,x==﹣a,
∴线段AD的长是方程x2+2ax﹣b2=0的一个根;
②∵AD=AE,
∴AE=EC=,
由勾股定理得,a2+b2=(b+a)2,
整理得, =.
一、选择题:
1、下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 ;B.2,3,4; C.4,6,7; D.5,11,12;
2、直角三角形有一条直角边长为6,另两条边长是连续偶数,则该三角形的周长为( )
A. 20 B. 22 C. 24 D. 26
3、如图,每个小正方形的边长为1,若是小正方形的顶点,则的度数为( )
A. 90? B. 60? C. 45? D. 30?
4、等腰直角三角尺与直尺按如图位置摆放,且三角尺在直角顶点在直尺的一边上.若∠1=35°,则∠2的度数是( )
A.95° B.100° C.105° D.110°
5、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的面积为………( )
A.16㎝ B.15㎝ ;C.14㎝ ; D.9㎝;
6、在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
7、如图,一架云梯长25 m,斜靠在一面墙上,梯子底端离墙7m.如果梯子的顶端下滑4 m,那么梯子的底部在水平方向上滑动了( )
A. 4 m B. 6m C. 8 m D. 10 m
8、(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. B. C. D.
9、有五根小木棒,其长度分别为7、15、20、24、25,现将它们摆成两个直角三角形,其中摆放方法正确的是( )
10、如图所示,直线l上有三个正方形a,b,c,若正方形a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
11、(2018?温州)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A.20 B.24 C. D.
12、如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9中,正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
二、填空题:
13、直角三角形两直角边长分别为3和4,则它斜边上的高为
14、如图,在中,cm,cm,于点,则
cm.
15、已知两条线段的长分别为15 cm和8 cm,则当第三条线段的长取整数 cm时,这三条线段能组成一个直角三角形.
16、如图,在△ABC中,AB=AC=6,BC=7,E是BC上的一个动点(不与点B,C重合),△DEF≌△ABC,其中点A,B的对应点分别是点D,E.当点E运动时DE边始终经过点A.设EF与AC相交于点G,当△AEG是等腰三角形时,BE的长为 .
17、(2018?湘潭)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
18、(2018?吉林)如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 .
19、如图,有一圆柱体,它的高为8cm,底面半径为2cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm(π取3).
20、如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为 .
21、如图①是我国古代著名的“赵爽弦图”的示意图.它是由四个全等的直角三角形围成的。若,将四个直角三角形中边长为6的直角边分别向外延长一倍.得到如图②所示的“数学风车”,则这个风车的外围周长是 。
22、(2018?襄阳)已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
三、解答题:
23、如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.
24、某路段限速标志规定:小汽车在此路段上行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30米的C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离50米.
(1)求BC的长;
(2)这辆小汽车超速了吗?
25、为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?
26、如图所示,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再转向北走到4.5 km处往东一拐,仅走0.5 km就找到了宝藏.则登陆点A与宝藏埋藏点B之间的距离是多少?
27、(2018?杭州)如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.
(1)若∠A=28°,求∠ACD的度数.
(2)设BC=a,AC=b.
①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.
②若AD=EC,求的值.
一、选择题:
1、A
2、C
3、C
4、B
5、C
6、A
7、C
8、A
9、D
10、C
11、B
12、B
二、填空题:
13、12/5
14、8
15、17
16、1或13/7
17、x2+32=(10﹣x)2
18、(﹣1,0)
19、10
20、60
21、76
22、2或2
三、解答题:
23、24m2
24、解:(1)∵AC=30米 AB=50米
又∵三角形ABC为直角三角形,根据勾股定理:
AC2+BC2=AB2
∴BC=40米
(2)汽车的速度为40米÷2秒=20米/秒=72千米/时
∴这辆小汽车超速了
25、解:(1)连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
则S四边形ABCD=S△BAD+S△DBC=?AD?AB+DB?BC=×4×3+×12×5=36;
(2)所以需费用36×200=7200(元).
26、解:如图,过点B作BC⊥AD于点C,
则AC=4-2+0.5=2.5(km),BC=4.5+1.5=6(km).
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=2.52+62=6.52,∴AB=6.5(km).
答:登陆点A与宝藏埋藏点B之间的距离是6.5 km.
27、解:(1)∵∠ACB=90°,∠A=28°,
∴∠B=62°,
∵BD=BC,
∴∠BCD=∠BDC=59°,
∴∠ACD=90°﹣∠BCD=31°;
(2)①由勾股定理得,AB==,
∴AD=﹣a,
解方程x2+2ax﹣b2=0得,x==﹣a,
∴线段AD的长是方程x2+2ax﹣b2=0的一个根;
②∵AD=AE,
∴AE=EC=,
由勾股定理得,a2+b2=(b+a)2,
整理得, =.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
