八年级苏科版数学第3章《勾股定理》单元提高测试(含答案)
文档属性
| 名称 | 八年级苏科版数学第3章《勾股定理》单元提高测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 00:00:00 | ||
图片预览


文档简介
八年级苏科版数学第3章《勾股定理》同步提高测试
一、选择题:
1、一个底边长为16,底边上的高位6的等腰三角形的腰长为( )
A.8;B.9; C.10; D.13;
2、下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
A. 6、8、10 B. 5、12、13
C. 9、40、41 D. 7、9、12
3、如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
A.1个 B.2个 C.3个 D.4个
4、有六根细木棒,它们的长度分别是2,4,6,8,10,12(单位:cm).若从中取出三根,首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A. 2,4,8 B. 4,8,10
C. 6,8,10 D. 8,10,12
5、(2018?长沙)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
6、如图,在中,,,点在上,,,是上的动点,则的最小值为( )
A. 4 B. 5 C.6 D.7
7、如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不与端点B,C重合).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
8、长方形台球桌ABCD上,一球从AB边上某处P击出,分别撞击球桌的边BC、DA各1次后,又回到出发点P处,每次球撞击桌边时,撞击前后的路线与桌边所成的角相等(例如图∠α=∠β)若AB=3,BC=4,则此球所走路线的总长度(不计球的大小)为( )
A.不确定 B.12 C.11 D.10
9、如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.6cm; B.7cm; C.8cm; D.9cm;
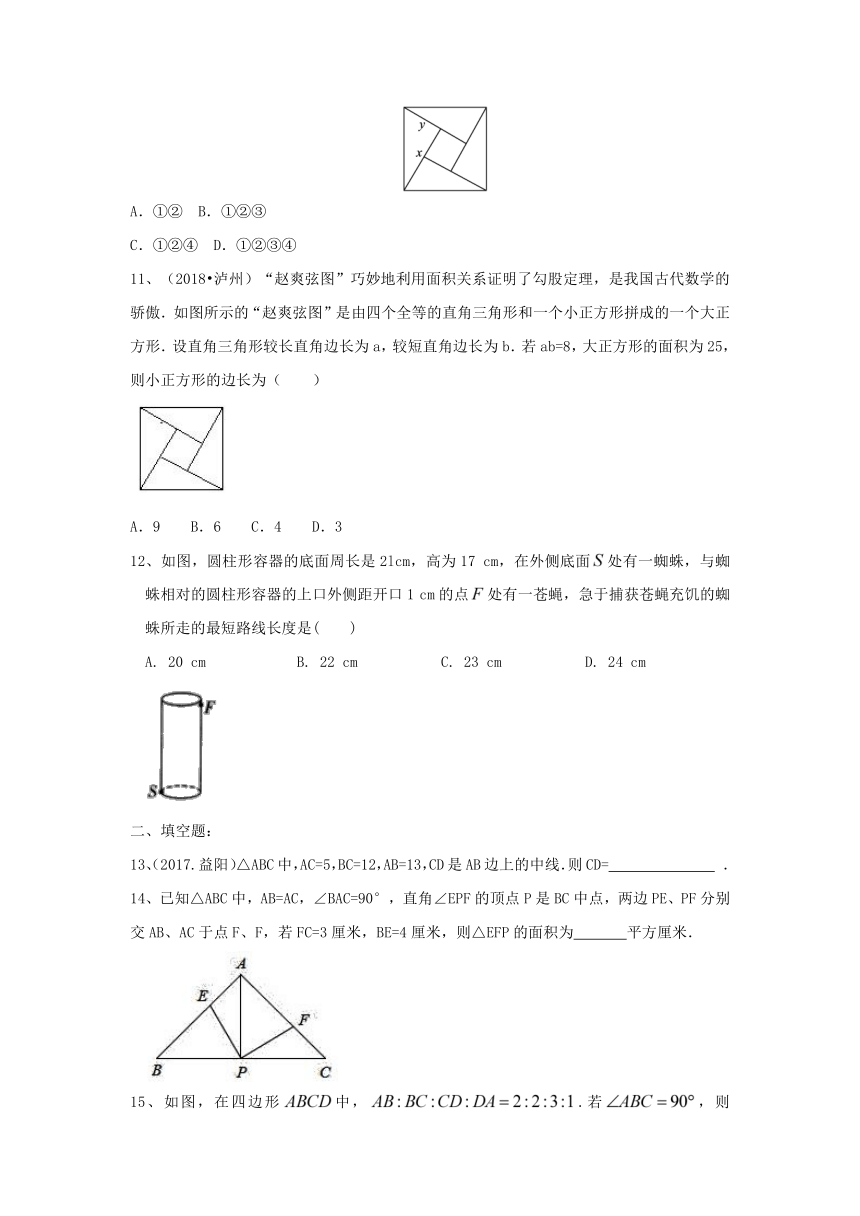
10、如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9中,正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
11、(2018?泸州)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
12、如图,圆柱形容器的底面周长是2lcm,高为17 cm,在外侧底面处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1 cm的点处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )
A. 20 cm B. 22 cm C. 23 cm D. 24 cm
二、填空题:
13、(2017.益阳)△ABC中,AC=5,BC=12,AB=13,CD是AB边上的中线.则CD= .
14、已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点F、F,若FC=3厘米,BE=4厘米,则△EFP的面积为 平方厘米.
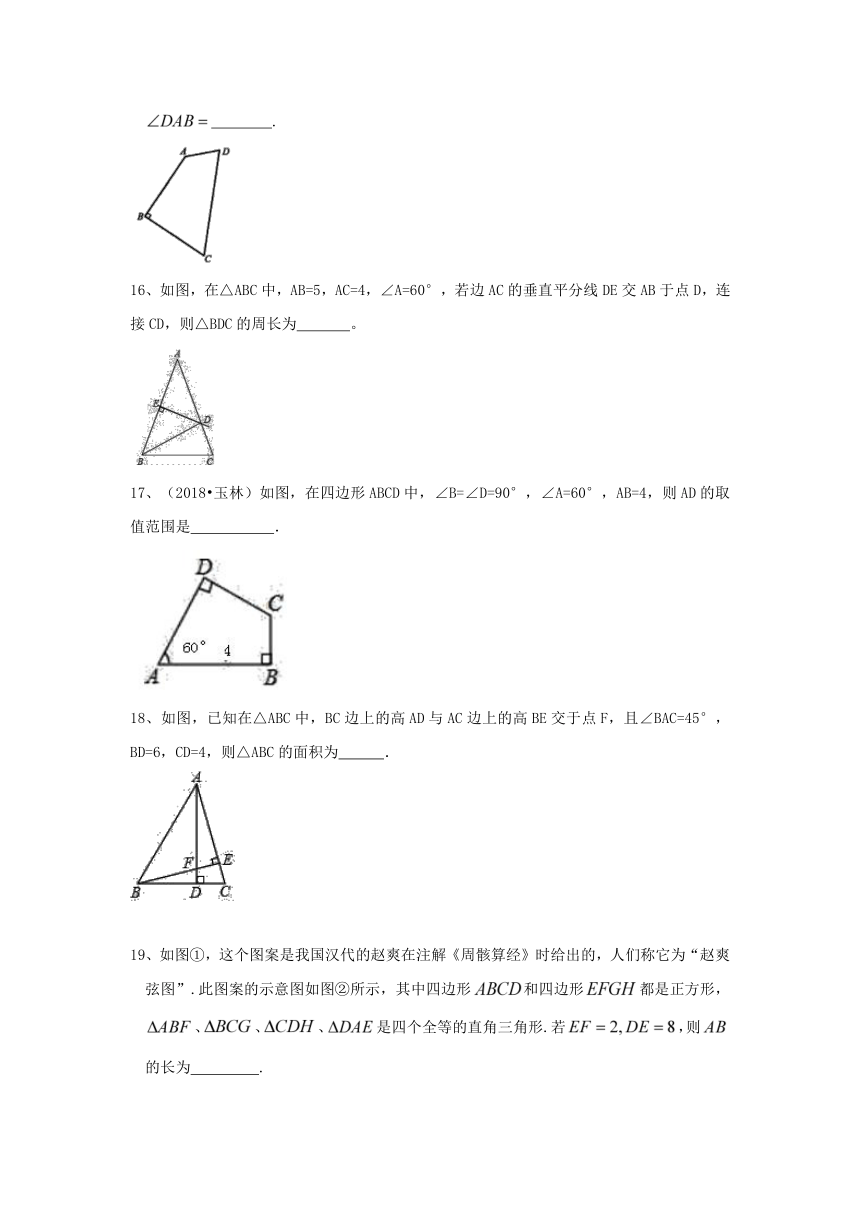
15、如图,在四边形中,.若,则 .
16、如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,则△BDC的周长为 。
17、(2018?玉林)如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是 .
18、如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为 .
19、如图①,这个图案是我国汉代的赵爽在注解《周骸算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②所示,其中四边形和四边形都是正方形,、、、是四个全等的直角三角形.若,则的长为 .
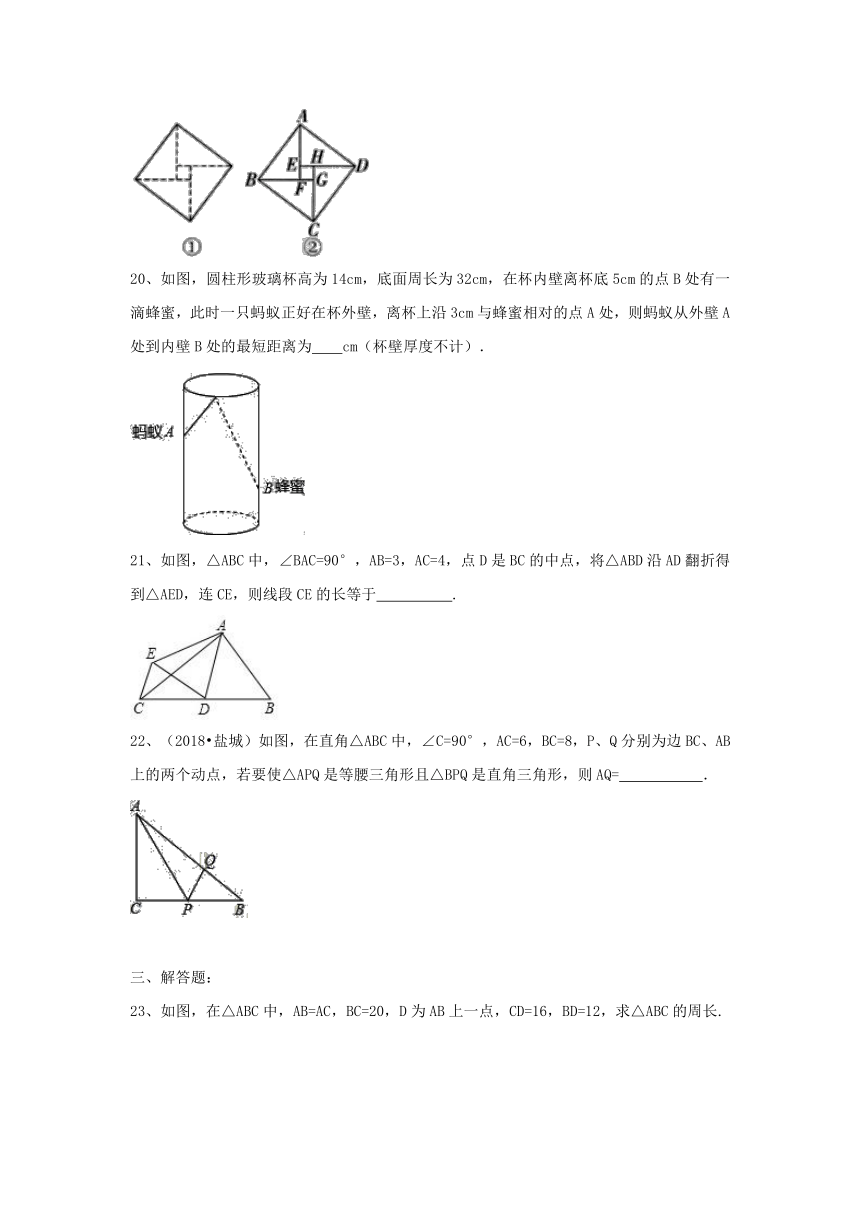
20、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
21、如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于 .
22、(2018?盐城)如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ= .
三、解答题:
23、如图,在△ABC中,AB=AC,BC=20,D为AB上一点,CD=16,BD=12,求△ABC的周长.
24、如图,在4×4正方形网格中,每个小正方形的边长都为1.
(1)求△ABC的周长;
(2)求证:∠ABC=90°.
25、如图,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.
(1)求BC的长;
(2)当点P,Q运动2 s时,求P,Q两点之间的距离;
(3)P,Q两点运动几秒时,AP=CQ?
26、如图,甲、乙两船同时从A港口出发,甲船以每小时30海里的速度向西偏北32°的方向航行2小时到达C岛,乙船以每小时40海里的速度航行2小时到B岛,已知B、C两岛相距100海里,求乙船航行的方向.
27、(2018?台湾)嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
答案:
一、选择题:
1、C
2、D
3、C
4、C
5、A
6、B
7、C
8、D
9、C
10、B
11、D
12、A
二、填空题:
13、6.5
14、25/4
15、135°
16、5+√21
17、2<AD<8
18、60
19、10
20、20
21、7/5
22、15/4或30/7
三、解答题:
23、160/3
24、解:(1)AB==2,BC==,AC==5,
△ABC的周长=2++5=3+5,
(2)∵AC2=25,AB2=20,BC2=5,
∴AC2=AB2+BC2,
∴∠ABC=90°.
21.解:(1)∵∠C=90°,AB=2.5,BC=0.7,
∴AC===2.4(米),
答:此时梯顶A距地面的高度AC是2.4米;
(2)∵梯子的顶端A下滑了0.9米至点A′,
∴A′C=AC﹣A′A=2.4﹣0.9=1.5(m),
在Rt△A′CB′中,由勾股定理得:A′C2+B′C2=A′B′2,
即1.52+B′C2=2.52,
∴B′C=2(m),
∴BB′=CB′﹣BC=2﹣0.7=1.3(m),
答:梯子的底端B在水平方向滑动了1.3m.
25、解:(1)∵在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm,∴BC2=AC2-AB2=252-72=242,∴BC=24 cm.
(2)连接PQ,
由题意知BP=7-2=5(cm),BQ=6×2=12(cm),
在Rt△BPQ中,由勾股定理,得PQ=BP2+BQ2=52+122=132,∴PQ=13 cm.
(3)设P,Q两点运动t s时,AP=CQ,则t=24-6t,
解得t=.
答:P,Q两点运动 s时,AP=CQ.
26、解:由题意得:甲2小时的路程=30×2=60海里,乙2小时的路程=40×2=80海里,且BC=100海里,
∵AC2+AB2=602+802=10000,
BC2=1002=10000,
∴AC2+AB2=BC2,
∴∠BAC=90°,
∵C岛在A西偏北32°方向,
∴B岛在A东偏北58°方向.
∴乙船航行的方向是东偏北58°方向.
27、解:第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
一、选择题:
1、一个底边长为16,底边上的高位6的等腰三角形的腰长为( )
A.8;B.9; C.10; D.13;
2、下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
A. 6、8、10 B. 5、12、13
C. 9、40、41 D. 7、9、12
3、如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
A.1个 B.2个 C.3个 D.4个
4、有六根细木棒,它们的长度分别是2,4,6,8,10,12(单位:cm).若从中取出三根,首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A. 2,4,8 B. 4,8,10
C. 6,8,10 D. 8,10,12
5、(2018?长沙)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
6、如图,在中,,,点在上,,,是上的动点,则的最小值为( )
A. 4 B. 5 C.6 D.7
7、如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不与端点B,C重合).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
8、长方形台球桌ABCD上,一球从AB边上某处P击出,分别撞击球桌的边BC、DA各1次后,又回到出发点P处,每次球撞击桌边时,撞击前后的路线与桌边所成的角相等(例如图∠α=∠β)若AB=3,BC=4,则此球所走路线的总长度(不计球的大小)为( )
A.不确定 B.12 C.11 D.10
9、如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.6cm; B.7cm; C.8cm; D.9cm;
10、如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边(x>y),则下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9中,正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
11、(2018?泸州)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
12、如图,圆柱形容器的底面周长是2lcm,高为17 cm,在外侧底面处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1 cm的点处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )
A. 20 cm B. 22 cm C. 23 cm D. 24 cm
二、填空题:
13、(2017.益阳)△ABC中,AC=5,BC=12,AB=13,CD是AB边上的中线.则CD= .
14、已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点F、F,若FC=3厘米,BE=4厘米,则△EFP的面积为 平方厘米.
15、如图,在四边形中,.若,则 .
16、如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,则△BDC的周长为 。
17、(2018?玉林)如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是 .
18、如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为 .
19、如图①,这个图案是我国汉代的赵爽在注解《周骸算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②所示,其中四边形和四边形都是正方形,、、、是四个全等的直角三角形.若,则的长为 .
20、如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
21、如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于 .
22、(2018?盐城)如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P、Q分别为边BC、AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ= .
三、解答题:
23、如图,在△ABC中,AB=AC,BC=20,D为AB上一点,CD=16,BD=12,求△ABC的周长.
24、如图,在4×4正方形网格中,每个小正方形的边长都为1.
(1)求△ABC的周长;
(2)求证:∠ABC=90°.
25、如图,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.
(1)求BC的长;
(2)当点P,Q运动2 s时,求P,Q两点之间的距离;
(3)P,Q两点运动几秒时,AP=CQ?
26、如图,甲、乙两船同时从A港口出发,甲船以每小时30海里的速度向西偏北32°的方向航行2小时到达C岛,乙船以每小时40海里的速度航行2小时到B岛,已知B、C两岛相距100海里,求乙船航行的方向.
27、(2018?台湾)嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 编号 图例 行径位置
第一条路径 R1 _ A→C→D→B
第二条路径 R2 … A→E→D→F→B
第三条路径 R3 ▂ A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
答案:
一、选择题:
1、C
2、D
3、C
4、C
5、A
6、B
7、C
8、D
9、C
10、B
11、D
12、A
二、填空题:
13、6.5
14、25/4
15、135°
16、5+√21
17、2<AD<8
18、60
19、10
20、20
21、7/5
22、15/4或30/7
三、解答题:
23、160/3
24、解:(1)AB==2,BC==,AC==5,
△ABC的周长=2++5=3+5,
(2)∵AC2=25,AB2=20,BC2=5,
∴AC2=AB2+BC2,
∴∠ABC=90°.
21.解:(1)∵∠C=90°,AB=2.5,BC=0.7,
∴AC===2.4(米),
答:此时梯顶A距地面的高度AC是2.4米;
(2)∵梯子的顶端A下滑了0.9米至点A′,
∴A′C=AC﹣A′A=2.4﹣0.9=1.5(m),
在Rt△A′CB′中,由勾股定理得:A′C2+B′C2=A′B′2,
即1.52+B′C2=2.52,
∴B′C=2(m),
∴BB′=CB′﹣BC=2﹣0.7=1.3(m),
答:梯子的底端B在水平方向滑动了1.3m.
25、解:(1)∵在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm,∴BC2=AC2-AB2=252-72=242,∴BC=24 cm.
(2)连接PQ,
由题意知BP=7-2=5(cm),BQ=6×2=12(cm),
在Rt△BPQ中,由勾股定理,得PQ=BP2+BQ2=52+122=132,∴PQ=13 cm.
(3)设P,Q两点运动t s时,AP=CQ,则t=24-6t,
解得t=.
答:P,Q两点运动 s时,AP=CQ.
26、解:由题意得:甲2小时的路程=30×2=60海里,乙2小时的路程=40×2=80海里,且BC=100海里,
∵AC2+AB2=602+802=10000,
BC2=1002=10000,
∴AC2+AB2=BC2,
∴∠BAC=90°,
∵C岛在A西偏北32°方向,
∴B岛在A东偏北58°方向.
∴乙船航行的方向是东偏北58°方向.
27、解:第一条路径的长度为++=2+,
第二条路径的长度为++1+=+++1,
第三条路径的长度为+=2+,
∵2+<2+<+++1,
∴最长路径为A→E→D→F→B;最短路径为A→G→B.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
