沪科版九年级上册第21章二次函数与反比例函数 单元测试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册第21章二次函数与反比例函数 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 171.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-15 20:47:49 | ||
图片预览




文档简介
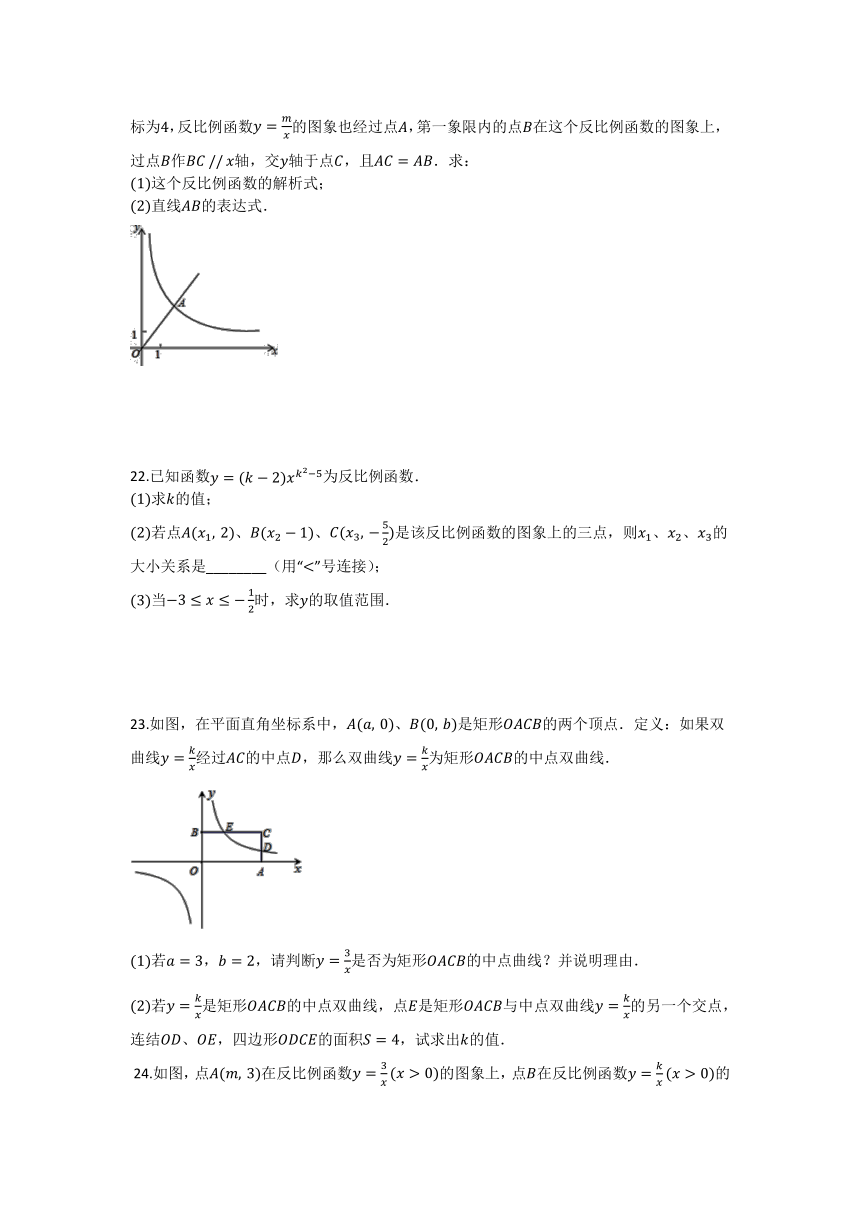
第21章 二次函数与反比例函数 单元检测试题
一、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.抛物线的部分图象如图所示,则当??<0时,??的取值范围是________.
/
?2.抛物线??=??
??
2
+????+??与??轴的公共点是(?2,?0),(6,?0),则此抛物线的对称轴是________.
?3.如图,点??是双曲线??=
4
3
??
(??>0)上动点,在??轴上取点??,使得以??、??、???为顶点的三角形是含有
30
°
角的直角三角形,则符合条件的点??的坐标是________.
/
?4.若点??(2,???)在反比例函数??=
4
??
的图象上,则??=________.
?5.心理学家发现,学生对概念的接受能力??与提出概念所用时间??(分)之间满足关系??=?0.1
??
2
+2.6??+43(0≤??≤30)??值越大,表示接受能力越强,在第________分钟时,学生接受能力最强.
?6.已知抛物线??=2
??
2
+3??+??,且当?1?7.已知二次函数??=??
??
2
+????+??(??≠0)的图象如图所示,有下列结论: ①
??
2
?4????>0;②??????>0;③8??+??>0;④9??+3??+??<0.?其中,正确结论的有________.
?/
8.如图,??是抛物线??=2(???2
)
2
对称轴上的一个动点,直线??=??平行??轴,分别与??=??、抛物线交于点??、??.若△??????是以点??或点??为直角顶点的等腰直角三角形,求满足条件的??的值,则??=________.
/
?9.把一个小球在离地面2??处向上抛起,上升的高度??(??)与时间??(??)的关系为??=10???5
??
2
,则小球运动到最高处时距离地面________??.
?10.一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做??点的横坐标,将该数的3倍记做??点的纵坐标.如图,抛物线??=?
??
2
+4??+5与??轴负半轴交于点??,点??(4,?5)在该抛物线上,则点??落在抛物线与直线????围成的区域内(阴影部分,含边界)的概率是________.
/
二、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,反比例函数??=
??
??
(??≠0)的图象经过点??(?2,?1),则??的值为( )
/
A.2
B.?2
C.±2
D.?4
?12.用20????长的绳子围成一个矩形,如果这个矩形的一边长为???????,面积是?????
??
2
,则??与??的函数关系式为( )
A.??=??(20???)
B.??=??(20?2??)
C.??=??(10???)
D.??=2??(10???)
?13.反比例函数??=?
2
??
与正比例函数??=????的一个交点为(?1,?2),则关于??的方程?
2
??
=????的解为( )
A.
??
1
=?1,
??
2
=1
B.
??
1
=?1,
??
2
=2
C.
??
1
=?2,
??
2
=1
D.
??
1
=?1,
??
2
=?2
14.对于反比例函数??=
??
??
,当??>0时,??随??的增大而增大,则二次函数??=??
??
2
+????的大致图象是( )
A./
B./
C./
D./
?15.购买??斤水果需24元,购买一斤水果的单价??与??的关系式是( )
A.??=
24
??
(??>0)
B.??=
24
??
(??为自然数)
C.??=
24
??
(??为整数)
D.??=
24
??
(??为正整数)
?16.如果等腰三角形的面积为10,底边长为??,底边上的高为??,则??与??的函数关系式为( )
A.??=
10
??
B.??=
5
??
C.??=
20
??
D.??=
??
20
?17.若按????/min的速度向容积为20的水池中注水,注满水池需??min.则所需时间??min与注水速度????/min之间的函数关系用图象大致表示为( )
A./
B./
C./
D./
?18.平面直角坐标系中,已知??(2,?1)、??(2,?6)两点,过反比例函数??=
??
??
的图象上任意一点??作??轴的垂线????,??为垂足,??为坐标原点.若反比例函数??=
??
??
的图象与线段????相交,则△??????面积??的取值范围是( )
A.
1
2
≤??≤3
B.1≤??≤6
C.2≤??≤12
D.??≤2或??≥12
?19.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度??(单位:????/
??
3
)与体积??(单位:
??
3
)满足函数关系式??=
??
??
(??为常数,??≠0),其图象如图所示,则??的值为( )
/
A.9
B.?9
C.4
D.?4
?20.如果函数??=?????2(??≠0)的图象不经过第一象限,那么函数??=
??
??
的图象一定在( )
A.第一,二象限
B.第三,四象限
C.第一,三象限
D.第二,四象限
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
21.已知:如图,在平面直角坐标系??????中,正比例函数??=
4
3
??的图象经过点??,点??的纵坐标为4,反比例函数??=
??
??
的图象也经过点??,第一象限内的点??在这个反比例函数的图象上,过点??作?????//???轴,交??轴于点??,且????=????.求: (1)这个反比例函数的解析式; (2)直线????的表达式.
/
?
22.已知函数??=(???2)
??
??
2
?5
为反比例函数.
(1)求??的值;
(2)若点??(
??
1
,?2)、??(
??
2
?1)、??(
??
3
,??
5
2
)是该反比例函数的图象上的三点,则
??
1
、
??
2
、
??
3
的大小关系是________(用“<”号连接);
(3)当?3≤??≤?
1
2
时,求??的取值范围.
?
23.如图,在平面直角坐标系中,??(??,?0)、??(0,???)是矩形????????的两个顶点.定义:如果双曲线??=
??
??
经过????的中点??,那么双曲线??=
??
??
为矩形????????的中点双曲线.
/
(1)若??=3,??=2,请判断??=
3
??
是否为矩形????????的中点曲线?并说明理由.
(2)若??=
??
??
是矩形????????的中点双曲线,点??是矩形????????与中点双曲线??=
??
??
的另一个交点,连结????、????,四边形????????的面积??=4,试求出??的值.
?24.如图,点??(??,?3)在反比例函数??=
3
??
(??>0)的图象上,点??在反比例函数??=
??
??
(??>0)的图象上,?????//???轴,过点??作????⊥??轴于点??,连接????与????相交于点??,且????=2????.
/
(1)求??的值;
(2)求反比例函数??=
??
??
的表达式.
?
25.如图,在平面直角坐标系中,直线??=2??+??(??<0)与坐标轴交于??.??两点,与双曲线??=
??
??
(??>0)交于点??,过点??作????⊥??轴,垂足为??,且点??是????的中点,连接????,
/
(1)如果??=?2,求双曲线的关系式;
(2)试探究??与??的数量关系,并求出直线????的关系式.
?
26.如图,已知点??在抛物线??=
1
8
??
2
上,点??(0,?2)在??轴上,直线??:??=?2与??轴交于点??,????⊥??于??
(1)如图1,若点??的横坐标为6,则????=________,????=________;
(2)当∠??????=
60
°
时,求??点的坐标;
(3)如图2,若点??为抛物线上任意一点(原点??除外),直线????交??于点??,过点??作????⊥??,交抛物线于点??,求证:直线????一定经过点??(0,?2).
/
答案
1.??>3或??2.??=2
3.(0,?2
3
)、(0,?2)、(0,?
8
3
3
)、(0,?8)
4.2
5.13
6.?59
8
7.①②③④
8.
5±
5
2
或1或3
9.7
10.
1
3
11-20:BCACA CBBAD
21.解:∵正比例函数??=
4
3
??的图象经过点??,点??的纵坐标为4, ∴点??的坐标为(3,?4), ∵反比例函数??=
??
??
的图象经过点??, ∴??=12, ∴反比例函数的解析式为:??=
12
??
; (2)如图,
/
连接????、????,作????⊥????于??, ∵????=????,????⊥????, ∴????=2????=6, ∴点??的坐标为:(6,?2), 设直线????的表达式为:??=????+??, 由题意得,
3??+??=4
6??+??=2
, 解得,
??=?
2
3
??=6
, ∴直线????的表达式为:??=?
2
3
??+6.
22.
??
1
<
??
3
<
??
2
.(3)把??=?3代入??=?
4
??
得:??=
4
3
, 把??=?
1
2
代入??=?
4
??
得:??=8, ∴??的取值范围是
4
3
≤??≤8.
23.解:(1)是, 理由: ??=3,??=2, ∴??(3,?0),??(0,?2), ∴??(3,?2), ∴????的中点坐标为(3,?1), 当??=3时,??=
3
??
=
3
3
=1, ∴????的中点在双曲线??=
3
??
的图象上, ∴??=
3
??
是为矩形????????的中点曲线.(2)如图,
/
∵点??,??在双曲线??=
??
??
的图象上, ∴
??
△??????
=
1
2
??,
??
△??????
=
1
2
??, ∵四边形????????的面积??=4, ∴矩形????????的面积=??+4, ∵??=
??
??
是矩形????????的中点双曲线, 设点??(??,???), ∴????=??,??(??,?2??), ∴矩形????????的面积为2????=2??, ∴2??=??+4, ∴??=4,
24.解:(1)∵点??(??,?3)在反比例函数??=
3
??
(??>0)的图象上, ∴3=
3
??
,解得??=1,
/
(2)过点??作????⊥??轴于??,延长线段????,交??轴于??, ∵?????//???轴, ∴????⊥??轴, ∴四边形????????是矩形,四边形????????是矩形, ∴????=????,????=????, ∴????=????, ∵点??在双曲线??=??=
3
??
(??>0)上, ∴
??
矩形????????
=3, 同理
??
矩形????????
=??, ∵?????//?????, ∴
????
????
=
????
????
=
1
2
, ∴????=2????, ∴????=2????, ∴
??
矩形????????
=3
??
矩形????????
=9, ∴??=9, ∴反比例函数??=
??
??
的表达式为??=
9
??
.
25.解:(1)当??=?2时, 直线??=2???2与坐标轴交点的坐标为??(1,?0),??(0,??2), ∵点??是????的中点, ∴????=2????=2, ∴??的横坐标为2, ∵点??在??=2???2上, ∴??=2×2?2=2, ∴点??的坐标为(2,?2). ∵点??在双曲线??=
??
??
(??>0)的图象上, ∴??=2×2=4, ∴双曲线的关系式??=
4
??
;(2)直线??=2??+??与坐标轴交点的坐标为??(?
??
2
,?0),??(0,???),∵点??是????的中点, ∴????=????,∵????⊥??轴, ∴∠??????=∠??????=
90
°
, 在△??????与△??????中,
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△???????△??????, ∴????=????,????=????, ∴点??的坐标为(???,????). ∵点??在双曲线??=
??
??
(??>0)的图象上, ∴??=(???)?(???)=
??
2
. 即??与??的数量关系为:??=
??
2
. 直线????的解析式为:??=??.
26.
13
2
13
2
(2)如图1中,作????⊥????于??,设??点坐标为(??,?
1
8
??
2
),则????=
??
2
+(
1
8
??
2
?2
)
2
=2+
1
8
??
2
,
/
∵????=2+
1
8
??
2
, ∴????=????, ∵∠??????=
60
°
, ∴△??????是等边三角形, ∵????=????,????⊥????, ∴????=????=4, ∴点??的纵坐标为6, 当??=6时,6=
1
8
??
2
, ∴??=±4
3
, ∴点??坐标为(?4
3
,?6)或(4
3
,?6).(3)证明:如图2中,设点??(??,?
1
8
??
2
),
/
∴直线????解析式为??=
??
8
??, ∵直线??=?2平行??轴, 令??=?2,则??=?
16
??
, ∴直线????与??交于??(?
16
??
,??2), ∵????⊥??,???//???轴, ∴??横坐标为?
16
??
, ∵点??在抛物线上, ∴??(?
16
??
,?
32
??
2
) 设直线????解析式为??=????+??, ∴
????+??=
1
8
??
2
?
16
??
???+??=
32
??
2
, 解得
??=
??
2
?16
8??
??=2
∴直线????解析式为??=
??
2
?16
8??
??+2, ∴直线????一定经过点??(0,?2).
一、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.抛物线的部分图象如图所示,则当??<0时,??的取值范围是________.
/
?2.抛物线??=??
??
2
+????+??与??轴的公共点是(?2,?0),(6,?0),则此抛物线的对称轴是________.
?3.如图,点??是双曲线??=
4
3
??
(??>0)上动点,在??轴上取点??,使得以??、??、???为顶点的三角形是含有
30
°
角的直角三角形,则符合条件的点??的坐标是________.
/
?4.若点??(2,???)在反比例函数??=
4
??
的图象上,则??=________.
?5.心理学家发现,学生对概念的接受能力??与提出概念所用时间??(分)之间满足关系??=?0.1
??
2
+2.6??+43(0≤??≤30)??值越大,表示接受能力越强,在第________分钟时,学生接受能力最强.
?6.已知抛物线??=2
??
2
+3??+??,且当?1?7.已知二次函数??=??
??
2
+????+??(??≠0)的图象如图所示,有下列结论: ①
??
2
?4????>0;②??????>0;③8??+??>0;④9??+3??+??<0.?其中,正确结论的有________.
?/
8.如图,??是抛物线??=2(???2
)
2
对称轴上的一个动点,直线??=??平行??轴,分别与??=??、抛物线交于点??、??.若△??????是以点??或点??为直角顶点的等腰直角三角形,求满足条件的??的值,则??=________.
/
?9.把一个小球在离地面2??处向上抛起,上升的高度??(??)与时间??(??)的关系为??=10???5
??
2
,则小球运动到最高处时距离地面________??.
?10.一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做??点的横坐标,将该数的3倍记做??点的纵坐标.如图,抛物线??=?
??
2
+4??+5与??轴负半轴交于点??,点??(4,?5)在该抛物线上,则点??落在抛物线与直线????围成的区域内(阴影部分,含边界)的概率是________.
/
二、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,反比例函数??=
??
??
(??≠0)的图象经过点??(?2,?1),则??的值为( )
/
A.2
B.?2
C.±2
D.?4
?12.用20????长的绳子围成一个矩形,如果这个矩形的一边长为???????,面积是?????
??
2
,则??与??的函数关系式为( )
A.??=??(20???)
B.??=??(20?2??)
C.??=??(10???)
D.??=2??(10???)
?13.反比例函数??=?
2
??
与正比例函数??=????的一个交点为(?1,?2),则关于??的方程?
2
??
=????的解为( )
A.
??
1
=?1,
??
2
=1
B.
??
1
=?1,
??
2
=2
C.
??
1
=?2,
??
2
=1
D.
??
1
=?1,
??
2
=?2
14.对于反比例函数??=
??
??
,当??>0时,??随??的增大而增大,则二次函数??=??
??
2
+????的大致图象是( )
A./
B./
C./
D./
?15.购买??斤水果需24元,购买一斤水果的单价??与??的关系式是( )
A.??=
24
??
(??>0)
B.??=
24
??
(??为自然数)
C.??=
24
??
(??为整数)
D.??=
24
??
(??为正整数)
?16.如果等腰三角形的面积为10,底边长为??,底边上的高为??,则??与??的函数关系式为( )
A.??=
10
??
B.??=
5
??
C.??=
20
??
D.??=
??
20
?17.若按????/min的速度向容积为20的水池中注水,注满水池需??min.则所需时间??min与注水速度????/min之间的函数关系用图象大致表示为( )
A./
B./
C./
D./
?18.平面直角坐标系中,已知??(2,?1)、??(2,?6)两点,过反比例函数??=
??
??
的图象上任意一点??作??轴的垂线????,??为垂足,??为坐标原点.若反比例函数??=
??
??
的图象与线段????相交,则△??????面积??的取值范围是( )
A.
1
2
≤??≤3
B.1≤??≤6
C.2≤??≤12
D.??≤2或??≥12
?19.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也随之改变.密度??(单位:????/
??
3
)与体积??(单位:
??
3
)满足函数关系式??=
??
??
(??为常数,??≠0),其图象如图所示,则??的值为( )
/
A.9
B.?9
C.4
D.?4
?20.如果函数??=?????2(??≠0)的图象不经过第一象限,那么函数??=
??
??
的图象一定在( )
A.第一,二象限
B.第三,四象限
C.第一,三象限
D.第二,四象限
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
21.已知:如图,在平面直角坐标系??????中,正比例函数??=
4
3
??的图象经过点??,点??的纵坐标为4,反比例函数??=
??
??
的图象也经过点??,第一象限内的点??在这个反比例函数的图象上,过点??作?????//???轴,交??轴于点??,且????=????.求: (1)这个反比例函数的解析式; (2)直线????的表达式.
/
?
22.已知函数??=(???2)
??
??
2
?5
为反比例函数.
(1)求??的值;
(2)若点??(
??
1
,?2)、??(
??
2
?1)、??(
??
3
,??
5
2
)是该反比例函数的图象上的三点,则
??
1
、
??
2
、
??
3
的大小关系是________(用“<”号连接);
(3)当?3≤??≤?
1
2
时,求??的取值范围.
?
23.如图,在平面直角坐标系中,??(??,?0)、??(0,???)是矩形????????的两个顶点.定义:如果双曲线??=
??
??
经过????的中点??,那么双曲线??=
??
??
为矩形????????的中点双曲线.
/
(1)若??=3,??=2,请判断??=
3
??
是否为矩形????????的中点曲线?并说明理由.
(2)若??=
??
??
是矩形????????的中点双曲线,点??是矩形????????与中点双曲线??=
??
??
的另一个交点,连结????、????,四边形????????的面积??=4,试求出??的值.
?24.如图,点??(??,?3)在反比例函数??=
3
??
(??>0)的图象上,点??在反比例函数??=
??
??
(??>0)的图象上,?????//???轴,过点??作????⊥??轴于点??,连接????与????相交于点??,且????=2????.
/
(1)求??的值;
(2)求反比例函数??=
??
??
的表达式.
?
25.如图,在平面直角坐标系中,直线??=2??+??(??<0)与坐标轴交于??.??两点,与双曲线??=
??
??
(??>0)交于点??,过点??作????⊥??轴,垂足为??,且点??是????的中点,连接????,
/
(1)如果??=?2,求双曲线的关系式;
(2)试探究??与??的数量关系,并求出直线????的关系式.
?
26.如图,已知点??在抛物线??=
1
8
??
2
上,点??(0,?2)在??轴上,直线??:??=?2与??轴交于点??,????⊥??于??
(1)如图1,若点??的横坐标为6,则????=________,????=________;
(2)当∠??????=
60
°
时,求??点的坐标;
(3)如图2,若点??为抛物线上任意一点(原点??除外),直线????交??于点??,过点??作????⊥??,交抛物线于点??,求证:直线????一定经过点??(0,?2).
/
答案
1.??>3或??2.??=2
3.(0,?2
3
)、(0,?2)、(0,?
8
3
3
)、(0,?8)
4.2
5.13
6.?59
8
7.①②③④
8.
5±
5
2
或1或3
9.7
10.
1
3
11-20:BCACA CBBAD
21.解:∵正比例函数??=
4
3
??的图象经过点??,点??的纵坐标为4, ∴点??的坐标为(3,?4), ∵反比例函数??=
??
??
的图象经过点??, ∴??=12, ∴反比例函数的解析式为:??=
12
??
; (2)如图,
/
连接????、????,作????⊥????于??, ∵????=????,????⊥????, ∴????=2????=6, ∴点??的坐标为:(6,?2), 设直线????的表达式为:??=????+??, 由题意得,
3??+??=4
6??+??=2
, 解得,
??=?
2
3
??=6
, ∴直线????的表达式为:??=?
2
3
??+6.
22.
??
1
<
??
3
<
??
2
.(3)把??=?3代入??=?
4
??
得:??=
4
3
, 把??=?
1
2
代入??=?
4
??
得:??=8, ∴??的取值范围是
4
3
≤??≤8.
23.解:(1)是, 理由: ??=3,??=2, ∴??(3,?0),??(0,?2), ∴??(3,?2), ∴????的中点坐标为(3,?1), 当??=3时,??=
3
??
=
3
3
=1, ∴????的中点在双曲线??=
3
??
的图象上, ∴??=
3
??
是为矩形????????的中点曲线.(2)如图,
/
∵点??,??在双曲线??=
??
??
的图象上, ∴
??
△??????
=
1
2
??,
??
△??????
=
1
2
??, ∵四边形????????的面积??=4, ∴矩形????????的面积=??+4, ∵??=
??
??
是矩形????????的中点双曲线, 设点??(??,???), ∴????=??,??(??,?2??), ∴矩形????????的面积为2????=2??, ∴2??=??+4, ∴??=4,
24.解:(1)∵点??(??,?3)在反比例函数??=
3
??
(??>0)的图象上, ∴3=
3
??
,解得??=1,
/
(2)过点??作????⊥??轴于??,延长线段????,交??轴于??, ∵?????//???轴, ∴????⊥??轴, ∴四边形????????是矩形,四边形????????是矩形, ∴????=????,????=????, ∴????=????, ∵点??在双曲线??=??=
3
??
(??>0)上, ∴
??
矩形????????
=3, 同理
??
矩形????????
=??, ∵?????//?????, ∴
????
????
=
????
????
=
1
2
, ∴????=2????, ∴????=2????, ∴
??
矩形????????
=3
??
矩形????????
=9, ∴??=9, ∴反比例函数??=
??
??
的表达式为??=
9
??
.
25.解:(1)当??=?2时, 直线??=2???2与坐标轴交点的坐标为??(1,?0),??(0,??2), ∵点??是????的中点, ∴????=2????=2, ∴??的横坐标为2, ∵点??在??=2???2上, ∴??=2×2?2=2, ∴点??的坐标为(2,?2). ∵点??在双曲线??=
??
??
(??>0)的图象上, ∴??=2×2=4, ∴双曲线的关系式??=
4
??
;(2)直线??=2??+??与坐标轴交点的坐标为??(?
??
2
,?0),??(0,???),∵点??是????的中点, ∴????=????,∵????⊥??轴, ∴∠??????=∠??????=
90
°
, 在△??????与△??????中,
∠??????=∠??????
????=????
∠??????=∠??????
, ∴△???????△??????, ∴????=????,????=????, ∴点??的坐标为(???,????). ∵点??在双曲线??=
??
??
(??>0)的图象上, ∴??=(???)?(???)=
??
2
. 即??与??的数量关系为:??=
??
2
. 直线????的解析式为:??=??.
26.
13
2
13
2
(2)如图1中,作????⊥????于??,设??点坐标为(??,?
1
8
??
2
),则????=
??
2
+(
1
8
??
2
?2
)
2
=2+
1
8
??
2
,
/
∵????=2+
1
8
??
2
, ∴????=????, ∵∠??????=
60
°
, ∴△??????是等边三角形, ∵????=????,????⊥????, ∴????=????=4, ∴点??的纵坐标为6, 当??=6时,6=
1
8
??
2
, ∴??=±4
3
, ∴点??坐标为(?4
3
,?6)或(4
3
,?6).(3)证明:如图2中,设点??(??,?
1
8
??
2
),
/
∴直线????解析式为??=
??
8
??, ∵直线??=?2平行??轴, 令??=?2,则??=?
16
??
, ∴直线????与??交于??(?
16
??
,??2), ∵????⊥??,???//???轴, ∴??横坐标为?
16
??
, ∵点??在抛物线上, ∴??(?
16
??
,?
32
??
2
) 设直线????解析式为??=????+??, ∴
????+??=
1
8
??
2
?
16
??
???+??=
32
??
2
, 解得
??=
??
2
?16
8??
??=2
∴直线????解析式为??=
??
2
?16
8??
??+2, ∴直线????一定经过点??(0,?2).
