北师大版八年级上册第三章 位置与坐标检测卷(含答案)
文档属性
| 名称 | 北师大版八年级上册第三章 位置与坐标检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 219.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-16 00:00:00 | ||
图片预览



文档简介
第三章检测卷
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1.某班级第3组第4排位置可以用数对(3,4)表示,则数对(1,2)表示的位置是( )
A.第2组第1排 B.第1组第1排
C.第1组第2排 D.第2组第2排
2.如图,在直角坐标系中阴影部分盖住的数可能是( )
A.(2,3) B.(-2,1)
C.(-2,-2.5) D.(3,-2)
3.如图,在正方形网格中,若A(1,1),B(2,0),则点C的坐标为( )
A.(-3,-2) B.(3,-2)
C.(-2,-3) D.(2,-3)
4.若点P(-m+2,m-1)在y轴上,则点P的坐标为( )
A.(0,-2) B.(1,0)
C.(0,1) D.(0,2)
5.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(小圆半径是1km).若小艇C相对于游船的位置可表示为(270°,-1.5),则描述图中另外两个小艇A,B的位置,正确的是( )
A.小艇A(60°,3),小艇B(-30°,2)
B.小艇A(60°,3),小艇B(60°,2)
6.已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
7.若点P(2-a,2a-1)到x轴的距离为3,则a的值为( )
A.2 B.-2
C.2或-1 D.-1
8.从车站向东走400m,再向北走500m到小红家;从车站向北走500m,再向西走200m到小强家.若以车站为原点,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,则小红家、小强家的坐标分别为( )
A.(400,500),(500,200) B.(400,500),(200,500)
C.(400,500),(-200,500) D.(500,400),(500,-200)
9.如图,直线BC经过原点O,点A在x轴上,AD⊥BC于D.若B(m,2),C(n,-3),A(2,0),则AD·BC的值为( )
A.不能确定 B.5
C.10 D.7
10.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
A.(-3,1) B.(-2,1)
C.(-4,1) D.(-2.5,1)
二、填空题(每小题3分,共24分)
11.若点P(x,y)满足xy<0,则点P在第________象限.
12.已知△ABC在直角坐标系中的位置如右图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为________.
13.若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是________.
14.若点P在第二象限,且到x轴、y轴的距离分别为3和4,则点P的坐标为________.
15.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b=________.
16.如果将点(-b,-a)称为点(a,b)的“反称点”,那么点(a,b)也是点(-b,-a)的“反称点”,此时称点(a,b)和点(-b,-a)互为“反称点”.容易发现,互为“反称点”的两点有时是重合的,例如(0,0)的“反称点”还是(0,0).请再写出一个这样的点:____________.
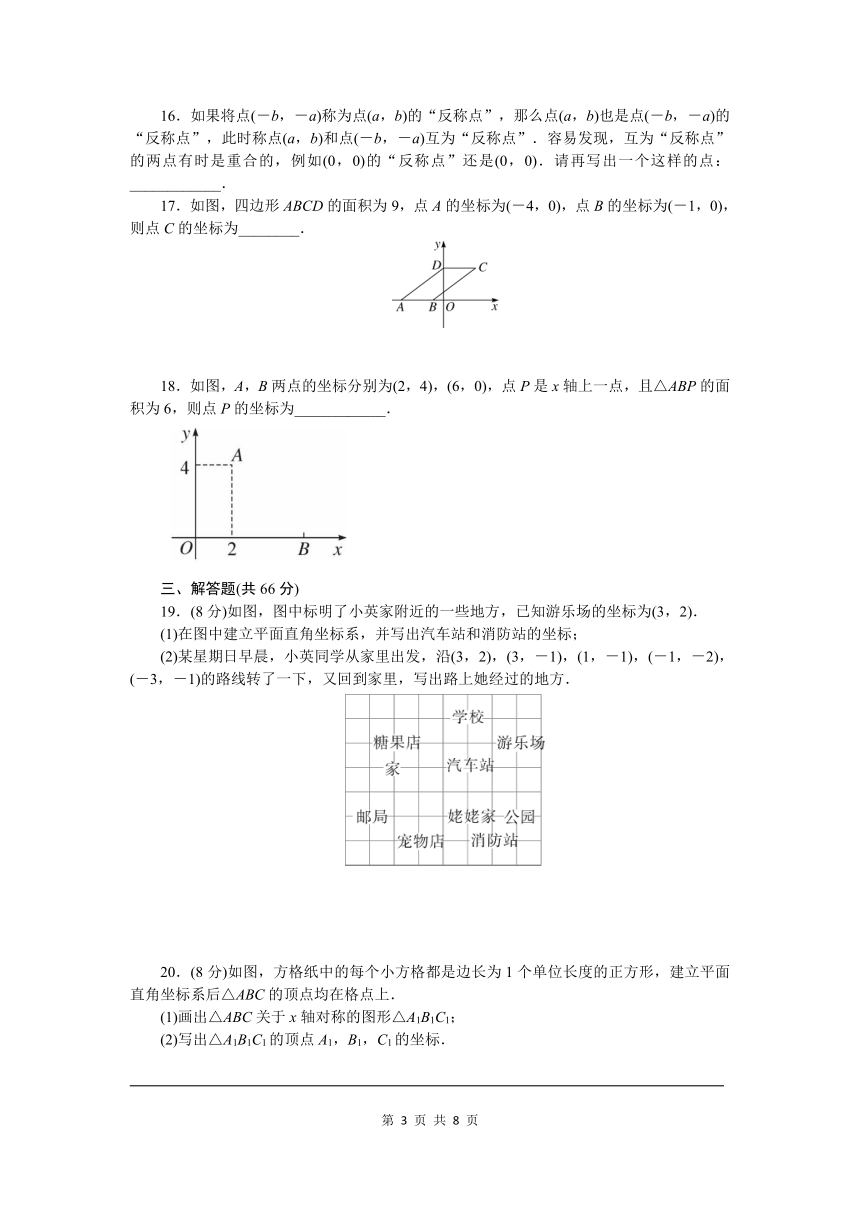
17.如图,四边形ABCD的面积为9,点A的坐标为(-4,0),点B的坐标为(-1,0),则点C的坐标为________.
18.如图,A,B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为____________.
三、解答题(共66分)
19.(8分)如图,图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).
(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
20.(8分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出△A1B1C1的顶点A1,B1,C1的坐标.
21.(8分)如图,正方形ABCD的边长为4,AD∥y轴,D(1,-1).
(1)写出A,B,C三个顶点的坐标;
(2)写出BC的中点P的坐标.
22.(8分)在平面直角坐标系中,已知A(2,a+3),B(b,b-3).
(1)当点A在第一象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴距离的2倍时,求点B所在的象限.
23.(10分)如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
24.(12分)已知A(0,1),B(2,0),C(4,3).
(1)在坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
25.(12分)如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
(4)观察图形,说出(3)中的关系在第三象限中是否存在?
答案
1.C 2.B 3.B 4.C 5.C 6.C 7.C 8.C
9.C 解析:根据三角形面积公式得S△ABC=AD·BC,而S△ABC=S△ABO+S△ACO=×2×2+×2×3=5,因此得到AD·BC=5,∴AD·BC=10.
10.A 解析:∵a,b满足关系式a=+2,∴b2-9=0,b+3≠0,∴b=3,a=2.∴点A(0,2),B(3,0),C(3,4).∵点B,C的横坐标都是3,∴BC∥y轴,∴BC=4-0=4,S三角形ABC=×4×3=6.∵OA=2,点P(m,1)在第二象限,∴S四边形ABOP=S三角形AOP+S三角形AOB=×2(-m)+×2×3=-m+3.∵S四边形ABOP=S三角形ABC,∴-m+3=6,解得m=-3,∴点P的坐标为(-3,1).故选A.
11.二或四 12.(4,2) 13.(3,-2) 14.(-4,3)
15.3 16.(-2,2)(答案不唯一) 17.(3,3)
18.(3,0)或(9,0) 解析:设点P的坐标为(x,0),根据题意得×4×|6-x|=6,解得x=3或9,所以点P的坐标为(3,0)或(9,0).
19.解:(1)建立平面直角坐标系如图所示;(2分)汽车站的坐标为(1,1),消防站的坐标为(2,-2).(4分)
(2)家→游乐场→公园→姥姥家→宠物店→邮局→家.(8分)
20.解:(1)作图略.(4分)
(2)A1(-1,-4),B1(-2,-2),C1(0,-1).(8分)
21.解:(1)A(1,3),B(-3,3),C(-3,-1).(6分)
(2)P(-3,1).(8分)
22.解:(1)由题意得a+3=2,解得a=-1.(3分)
(2)由题意得|b-3|=2|b|,解得b=-3或b=1.(5分)当b=-3时,b-3=-6,点B(-3,-6)在第三象限;当b=1时,b-3=-2,点B(1,-2)在第四象限.(8分)
23.解:(1)过B作BF⊥x轴于F,过A作AG⊥x轴于G,如图所示.(2分)∴S四边形ABCO=S三角形BCF+S梯形ABFG+S三角形AGO=×102=2500(平方米).(6分)
(2)把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,即将这个四边形向右平移2个单位长度,(8分)故所得到的四边形的面积与原四边形的面积相等,为2500平方米.(10分)
24.解:(1)△ABC如图所示.(3分)
(2)如图,过点C向x轴、y轴作垂线,垂足分别为D,E.(4分)∴S长方形DOEC=3×4=12,S△BCD=×2×3=3,S△ACE=×2×4=4,S△AOB=×2×1=1.(6分)∴S△ABC=S长方形DOEC-S△ACE-S△BCD-S△AOB=12-4-3-1=4.(7分)
(3)当点P在x轴上时,S△ABP=AO·BP=4,即×1·BP=4,解得BP=8.∵点B的坐标为(2,0).∴点P的坐标为(10,0)或(-6,0);(9分)当点P在y轴上时,S△ABP=BO·AP=4,即×2AP=4,解得AP=4.∵点A的坐标为(0,1),∴点P的坐标为(0,5)或(0,-3).(11分)综上所述,点P的坐标为(10,0)或(-6,0)或(0,5)或(0,-3).(12分)
25.解:(1)
(2)如图所示.(6分)
(3)第一象限内的拐点的横坐标与纵坐标相等.(9分)
(4)存在.(12分)
时间:120分钟 满分:120分
一、选择题(每小题3分,共30分)
1.某班级第3组第4排位置可以用数对(3,4)表示,则数对(1,2)表示的位置是( )
A.第2组第1排 B.第1组第1排
C.第1组第2排 D.第2组第2排
2.如图,在直角坐标系中阴影部分盖住的数可能是( )
A.(2,3) B.(-2,1)
C.(-2,-2.5) D.(3,-2)
3.如图,在正方形网格中,若A(1,1),B(2,0),则点C的坐标为( )
A.(-3,-2) B.(3,-2)
C.(-2,-3) D.(2,-3)
4.若点P(-m+2,m-1)在y轴上,则点P的坐标为( )
A.(0,-2) B.(1,0)
C.(0,1) D.(0,2)
5.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(小圆半径是1km).若小艇C相对于游船的位置可表示为(270°,-1.5),则描述图中另外两个小艇A,B的位置,正确的是( )
A.小艇A(60°,3),小艇B(-30°,2)
B.小艇A(60°,3),小艇B(60°,2)
6.已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
7.若点P(2-a,2a-1)到x轴的距离为3,则a的值为( )
A.2 B.-2
C.2或-1 D.-1
8.从车站向东走400m,再向北走500m到小红家;从车站向北走500m,再向西走200m到小强家.若以车站为原点,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,则小红家、小强家的坐标分别为( )
A.(400,500),(500,200) B.(400,500),(200,500)
C.(400,500),(-200,500) D.(500,400),(500,-200)
9.如图,直线BC经过原点O,点A在x轴上,AD⊥BC于D.若B(m,2),C(n,-3),A(2,0),则AD·BC的值为( )
A.不能确定 B.5
C.10 D.7
10.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
A.(-3,1) B.(-2,1)
C.(-4,1) D.(-2.5,1)
二、填空题(每小题3分,共24分)
11.若点P(x,y)满足xy<0,则点P在第________象限.
12.已知△ABC在直角坐标系中的位置如右图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为________.
13.若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是________.
14.若点P在第二象限,且到x轴、y轴的距离分别为3和4,则点P的坐标为________.
15.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b=________.
16.如果将点(-b,-a)称为点(a,b)的“反称点”,那么点(a,b)也是点(-b,-a)的“反称点”,此时称点(a,b)和点(-b,-a)互为“反称点”.容易发现,互为“反称点”的两点有时是重合的,例如(0,0)的“反称点”还是(0,0).请再写出一个这样的点:____________.
17.如图,四边形ABCD的面积为9,点A的坐标为(-4,0),点B的坐标为(-1,0),则点C的坐标为________.
18.如图,A,B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为____________.
三、解答题(共66分)
19.(8分)如图,图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).
(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
20.(8分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出△A1B1C1的顶点A1,B1,C1的坐标.
21.(8分)如图,正方形ABCD的边长为4,AD∥y轴,D(1,-1).
(1)写出A,B,C三个顶点的坐标;
(2)写出BC的中点P的坐标.
22.(8分)在平面直角坐标系中,已知A(2,a+3),B(b,b-3).
(1)当点A在第一象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴距离的2倍时,求点B所在的象限.
23.(10分)如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
24.(12分)已知A(0,1),B(2,0),C(4,3).
(1)在坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
25.(12分)如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
(4)观察图形,说出(3)中的关系在第三象限中是否存在?
答案
1.C 2.B 3.B 4.C 5.C 6.C 7.C 8.C
9.C 解析:根据三角形面积公式得S△ABC=AD·BC,而S△ABC=S△ABO+S△ACO=×2×2+×2×3=5,因此得到AD·BC=5,∴AD·BC=10.
10.A 解析:∵a,b满足关系式a=+2,∴b2-9=0,b+3≠0,∴b=3,a=2.∴点A(0,2),B(3,0),C(3,4).∵点B,C的横坐标都是3,∴BC∥y轴,∴BC=4-0=4,S三角形ABC=×4×3=6.∵OA=2,点P(m,1)在第二象限,∴S四边形ABOP=S三角形AOP+S三角形AOB=×2(-m)+×2×3=-m+3.∵S四边形ABOP=S三角形ABC,∴-m+3=6,解得m=-3,∴点P的坐标为(-3,1).故选A.
11.二或四 12.(4,2) 13.(3,-2) 14.(-4,3)
15.3 16.(-2,2)(答案不唯一) 17.(3,3)
18.(3,0)或(9,0) 解析:设点P的坐标为(x,0),根据题意得×4×|6-x|=6,解得x=3或9,所以点P的坐标为(3,0)或(9,0).
19.解:(1)建立平面直角坐标系如图所示;(2分)汽车站的坐标为(1,1),消防站的坐标为(2,-2).(4分)
(2)家→游乐场→公园→姥姥家→宠物店→邮局→家.(8分)
20.解:(1)作图略.(4分)
(2)A1(-1,-4),B1(-2,-2),C1(0,-1).(8分)
21.解:(1)A(1,3),B(-3,3),C(-3,-1).(6分)
(2)P(-3,1).(8分)
22.解:(1)由题意得a+3=2,解得a=-1.(3分)
(2)由题意得|b-3|=2|b|,解得b=-3或b=1.(5分)当b=-3时,b-3=-6,点B(-3,-6)在第三象限;当b=1时,b-3=-2,点B(1,-2)在第四象限.(8分)
23.解:(1)过B作BF⊥x轴于F,过A作AG⊥x轴于G,如图所示.(2分)∴S四边形ABCO=S三角形BCF+S梯形ABFG+S三角形AGO=×102=2500(平方米).(6分)
(2)把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,即将这个四边形向右平移2个单位长度,(8分)故所得到的四边形的面积与原四边形的面积相等,为2500平方米.(10分)
24.解:(1)△ABC如图所示.(3分)
(2)如图,过点C向x轴、y轴作垂线,垂足分别为D,E.(4分)∴S长方形DOEC=3×4=12,S△BCD=×2×3=3,S△ACE=×2×4=4,S△AOB=×2×1=1.(6分)∴S△ABC=S长方形DOEC-S△ACE-S△BCD-S△AOB=12-4-3-1=4.(7分)
(3)当点P在x轴上时,S△ABP=AO·BP=4,即×1·BP=4,解得BP=8.∵点B的坐标为(2,0).∴点P的坐标为(10,0)或(-6,0);(9分)当点P在y轴上时,S△ABP=BO·AP=4,即×2AP=4,解得AP=4.∵点A的坐标为(0,1),∴点P的坐标为(0,5)或(0,-3).(11分)综上所述,点P的坐标为(10,0)或(-6,0)或(0,5)或(0,-3).(12分)
25.解:(1)
(2)如图所示.(6分)
(3)第一象限内的拐点的横坐标与纵坐标相等.(9分)
(4)存在.(12分)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
