24.1.4 圆周角课时作业（2）

24.1.4 圆周角课时作业（2）
姓名：__________班级：__________考号：__________
一 、选择题
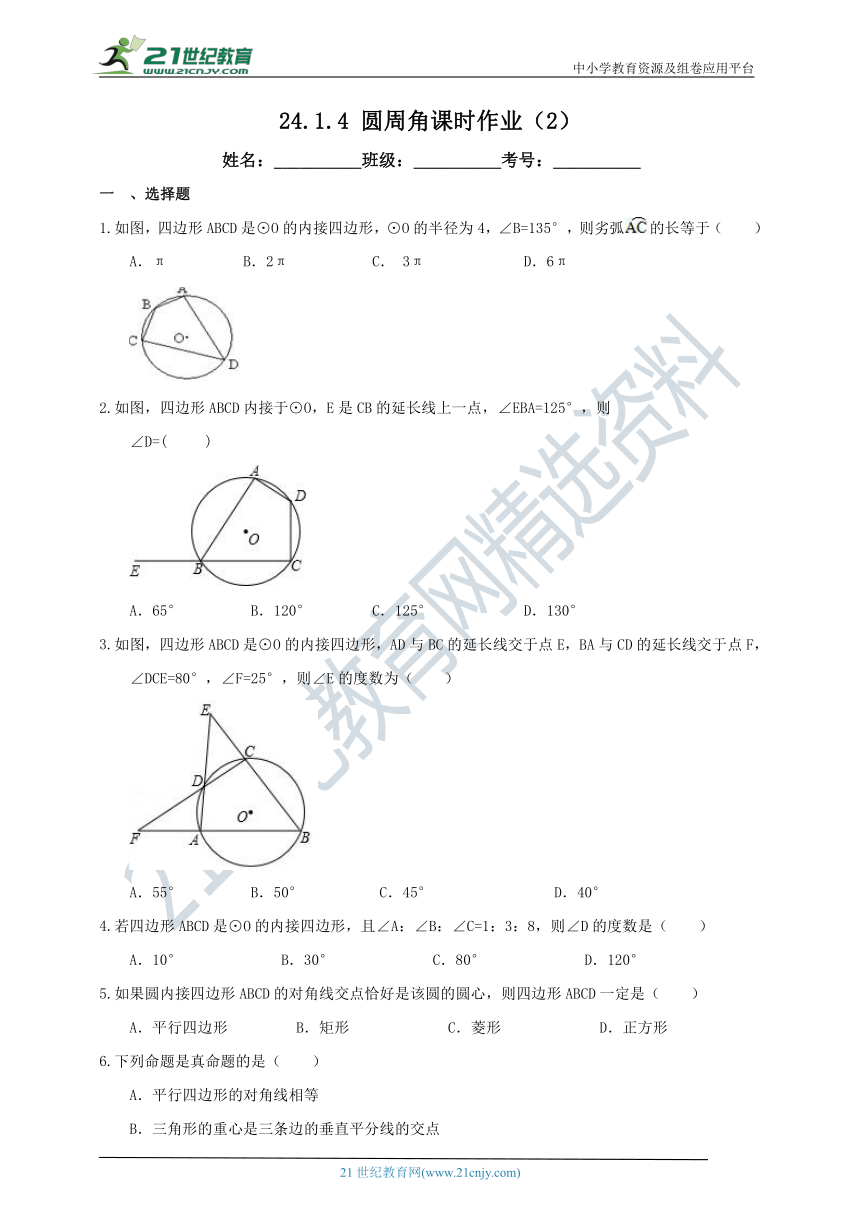
1.如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则劣弧的长等于（ ）　　
A．π B．2π C． 3π D．6π
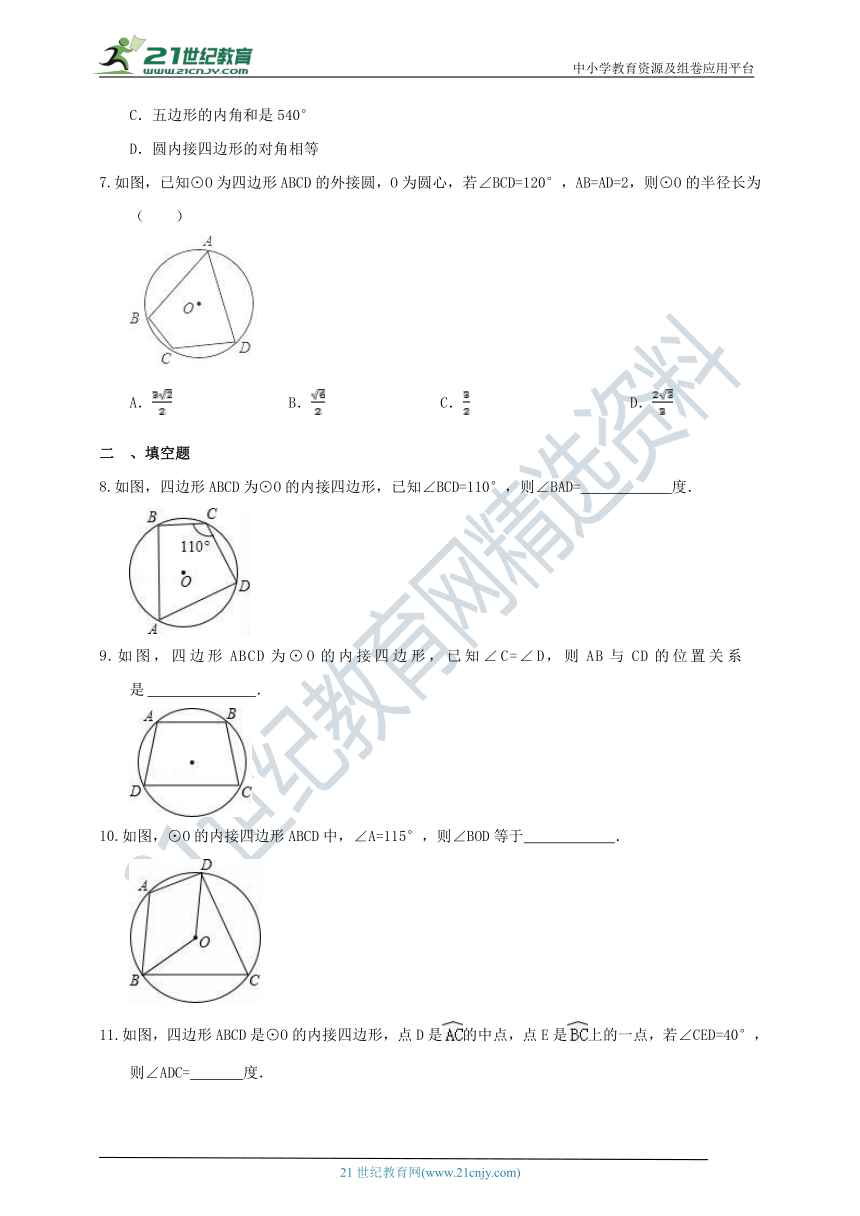
2.如图，四边形ABCD内接于⊙O，E是CB的延长线上一点，∠EBA=125°，则
∠D=( )
A．65° B．120° C．125° D．130°
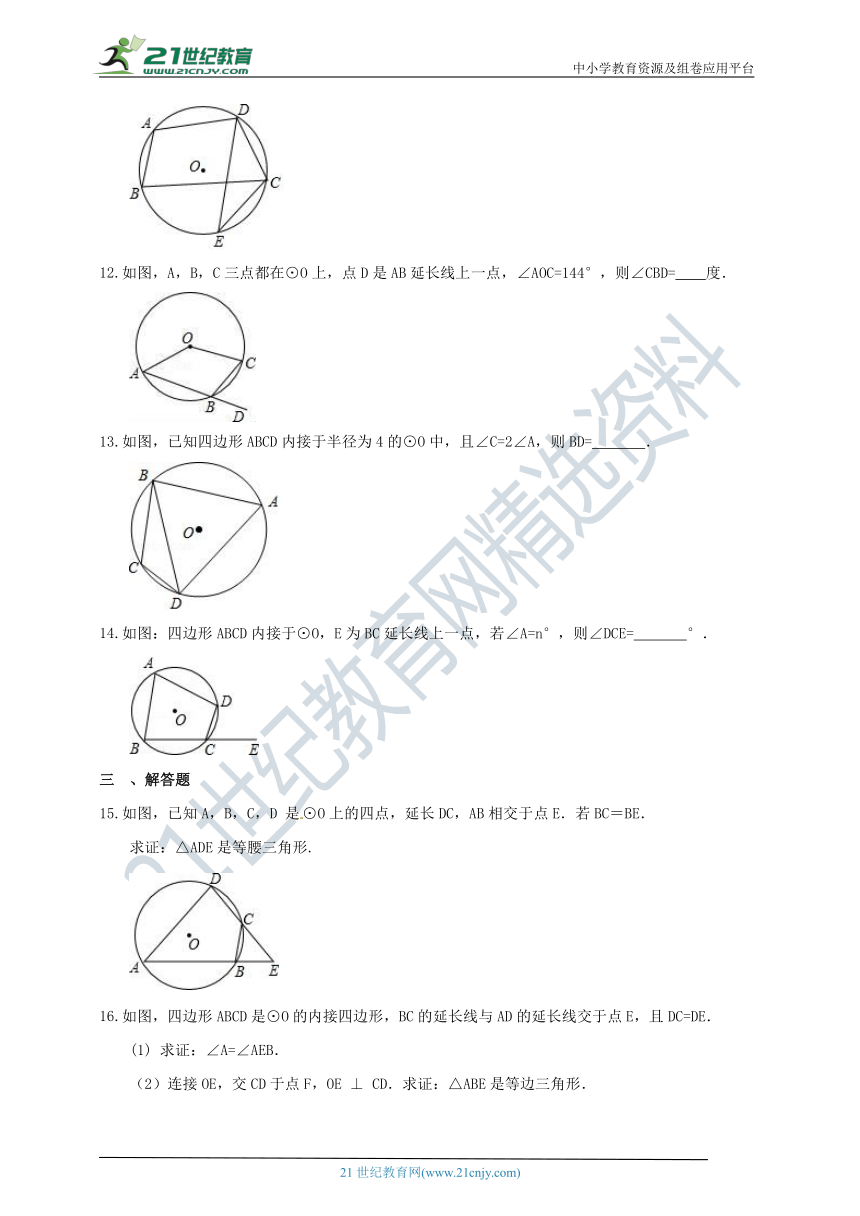
3.如图，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，∠DCE=80°，∠F=25°，则∠E的度数为（　　）
A．55° B．50° C．45° D．40°
4.若四边形ABCD是⊙O的内接四边形，且∠A：∠B：∠C=1：3：8，则∠D的度数是（　　）
A．10° B．30° C．80° D．120°
5.如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心，则四边形ABCD一定是（　　）
A．平行四边形 B．矩形 C．菱形 D．正方形
6.下列命题是真命题的是（　　）
A．平行四边形的对角线相等
B．三角形的重心是三条边的垂直平分线的交点
C．五边形的内角和是540°
D．圆内接四边形的对角相等
7.如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（　　）
A． B． C． D．
二 、填空题
8.如图，四边形ABCD为⊙O的内接四边形，已知∠BCD=110°，则∠BAD=　　　　　　度．
9.如图，四边形ABCD为⊙O的内接四边形，已知∠C=∠D，则AB与CD的位置关系是　　　　　　．
10.如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于　　　　　　．
11.如图，四边形ABCD是⊙O的内接四边形，点D是的中点，点E是上的一点，若∠CED=40°，则∠ADC=　 　度．
12.如图，A，B，C三点都在⊙O上，点D是AB延长线上一点，∠AOC=144°，则∠CBD=　　度．
13.如图，已知四边形ABCD内接于半径为4的⊙O中，且∠C=2∠A，则BD=　 　．
14.如图：四边形ABCD内接于⊙O，E为BC延长线上一点，若∠A=n°，则∠DCE=　 　°．
三 、解答题
15.如图，已知A，B，C，D 是⊙O上的四点，延长DC，AB相交于点E．若BC＝BE．
求证：△ADE是等腰三角形.
16.如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．
(1) 求证：∠A=∠AEB．
（2）连接OE，交CD于点F，OE ⊥ CD．求证：△ABE是等边三角形．

17.在△ABC中，CE，BD分别是边AB，AC上的高，F是BC边上的中点．
（1）指出图中的一个等腰三角形，并说明理由．
（2）若∠A=x°，求∠EFD的度数（用含x的代数式表达）．
（3）猜想∠ABC和∠EDA的数量关系，并证明．
18.如图，⊙的内接四边形ABCD两组对边的延长线分别相交于点E、F
（1）若∠E=∠F时，求证：∠ADC=∠ABC；
（2）若∠E=∠F=42°时，求∠A的度数；
（3）若∠E=α，∠F=β，且。α≠β.请你用含有α、β的代数式表示∠A的大小.
答案解析
一 、选择题
1.【考点】圆内接四边形的性质
【分析】连接OA、OC，然后根据圆周角定理求得∠AOC的度数，最后根据弧长公式求解．
解：∵四边形ABCD是⊙O的内接四边形，∠B=135°，
∴∠D=45°，
∴劣弧的度数是90°，
又∵⊙O的半径为4，
∴=，
故选：B．
2.【考点】圆内接四边形的性质．
【分析】先求出∠ABC，根据圆内接四边形的对角互补求出即可．
解：∵∠EBA=125°，
∴∠ABC=180°﹣125°=55°，
∵四边形ABCD内接于⊙O，
∴∠D+∠ABC=180°，
∴∠D=180°﹣55°=125°，
故选C．
【点评】本题考查了圆内接四边形的性质的应用，注意：圆内接四边形的对角互补，难度适中．
3.【考点】圆内接四边形的性质；圆周角定理．
【分析】根据三角形的外角的性质求出∠B，根据圆内接四边形的性质和三角形内角和定理计算即可．
解：∠B=∠DCE﹣∠F=55°，
∵四边形ABCD是⊙O的内接四边形，
∴∠EDC=∠B=55°，
∴∠E=180°﹣∠DCE﹣∠EDC=45°，
故选：C．
4.【考点】圆内接四边形的性质．
【分析】题可设∠A=x，则∠B=3x，∠C=8x；利用圆内接四边形的对角互补，可求出∠A、∠C的度数，进而求出∠B和∠D的度数，由此得解．
解：设∠A=x，则∠B=3x，∠C=8x，
因为四边形ABCD为圆内接四边形，
所以∠A+∠C=180°，
即：x+8x=180，
∴x=20°，
则∠A=20°，∠B=60°，∠C=160°，
所以∠D=120°，
故选D．
5.【考点】圆内接四边形的性质．
【分析】由圆内接四边形ABCD的对角线交点恰好是该圆的圆心，根据直径所对的圆周角是直角，可求得四边形ABCD的四个内角都是直角，即可判定四边形ABCD一定是矩形．
解：∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心，
∴∠A=∠B=∠C=∠D=90°，
∴四边形ABCD一定是矩形．
故选B．
6.【考点】命题与定理
【分析】根据正多边形的内角和的计算公式、矩形的性质、菱形的判定、圆内接四边形的性质判断即可．
解：正五边形的内角和=（5﹣2）×180°=540°，A是真命题；
矩形的对角线相等，B是真命题；
对角线互相垂直的平行四边形是菱形，C是假命题；
圆内接四边形的对角互补，D是真命题；
故选：C．
【点评】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
7.【考点】 圆内接四边形的性质．.
【分析】连接BD，作OE⊥AD，连接OD，先由圆内接四边形的性质求出∠BAD的度数，再由AD=AB可得出△ABD是等边三角形，则DE=AD，∠ODE=∠ADB=30°，根据锐角三角函数的定义即可得出结论．
解：连接BD，作OE⊥AD，连接OD，
∵⊙O为四边形ABCD的外接圆，∠BCD=120°，
∴∠BAD=60°．
∵AD=AB=2，
∴△ABD是等边三角形．
∴DE=AD=1，∠ODE=∠ADB=30°，
∴OD==．
故选D．
【点评】本题考查的是圆内接四边形的性质，熟知圆内接四边形对角互补是解答此题的关键．
二 、填空题
8.【考点】圆内接四边形的性质；圆周角定理．
【分析】根据圆内接四边形的对角互补求∠BAD的度数即可．
解：∵四边形ABCD为⊙O的内接四边形，
∴∠BCD+∠BAD=180°（圆内接四边形的对角互补）；
又∵∠BCD=110°，
∴∠BAD=70°．
故答案为：70．
9.【考点】圆内接四边形的性质．
【分析】由圆内接四边形的对角互补的性质以及等角的补角相等求解即可．
解：∵四边形ABCD为⊙O的内接四边形，
∴∠A+∠C=180°
又∵∠C=∠D，
∴∠A+∠D=180°．
∴AB∥CD．
故答案为：AB∥CD．
10.【考点】圆内接四边形的性质；圆周角定理．
【分析】根据圆内接四边形的对角互补求得∠C的度数，再根据圆周角定理求解即可．
解：∵∠A=115°
∴∠C=180°﹣∠A=65°
∴∠BOD=2∠C=130°．
故答案为：130°．
【点评】本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．
11.【考点】圆内接四边形的性质；圆周角定理．
【分析】先求出∠AEC，再用圆内接四边形的性质即可得出结论．
解：如图，
连接AE，
∵点D是的中点，
∴∠AED=∠CED，
∵∠CED=40°，
∴∠AEC=2∠CED=80°，
∵四边形ADCE是圆内接四边形，
∴∠ADC+∠AEC=180°，
∴∠ADC=180°﹣∠AEC=100°，
故答案为：100．
12.【考点】圆内接四边形的性质；圆周角定理．
【分析】首先在优弧AC上取点E，连接AE，CE，由圆周角定理可求得∠E的度数，又由圆的内接四边形的性质，可得∠CBD=∠E．
解：在优弧AC上取点E，连接AE，CE，
∵∠AOC=144°，
∴∠E=∠AOC=72°，
∵∠ABC=180°﹣∠E，∠ABC=180°﹣∠CBD，
∴∠CBD=∠E=72°．
故答案为：72°．
13.【考点】圆内接四边形的性质；解直角三角形．
【分析】连接OD、OB，过点O作OF⊥BD，垂足为F，由垂径定理可知DF=BF，∠DOF=∠BOF，再由圆内接四边形的性质求出∠A的度数，故可得出∠BOD的度数，再由锐角三角函数的定义求出BF的长，进而可得出结论．
解：连接OD、OB，过点O作OF⊥BD，垂足为F，
∵OF⊥BD，
∴DF=BF，∠DOF=∠BOF．
∵四边形ABCD内接于⊙O，
∴∠A+∠C=180°．
∵∠C=2∠A，
∴∠A=60°，
∴∠BOD=120°，
∴∠BOF=60°．
∵OB=4，
∴BF=OB?sin∠BOF=4×sin60°=2，
∴BD=2BF=4．
故答案为：4．
14.【考点】圆内接四边形的性质
【分析】利用圆内接四边形的对角互补和邻补角的性质求解．
解：∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠DCB=180°，
又∵∠DCE+∠DCB=180°
∴∠DCE=∠A=n°
故答案为：n
【点评】本题考查了圆内接四边形的性质．解决本题的关键是掌握：圆内接四边形的对角互补．
三 、解答题
15.【考点】圆内接四边形的性质,等腰三角形的判定
【分析】求出∠A=∠BCE=∠E，即可得出AD=DE，从而判定等腰三角形．
证明：∵BC＝BE，
∴∠E＝∠BCE.
∵ 四边形ABCD是圆内接四边形，
∴∠A＋∠DCB＝180°.
∵∠BCE＋∠DCB＝180°,
∴∠A＝∠BCE.
∴∠A＝∠E.
∴ AD＝DE.
∴△ADE是等腰三角形
【点评】考查了圆内接四边形的性质、等腰三角形的判定的知识，属于基础题，相对比较简单．
16.【考点】圆内接四边形的性质；等边三角形的判定与性质；圆周角定理．.
【分析】（1）根据圆内接四边形的性质可得∠A+∠BCD=180°，根据邻补角互补可得∠DCE+∠BCD=180°，进而得到∠A=∠DCE，然后利用等边对等角可得∠DCE=∠AEB，进而可得∠A=∠AEB；
（2）首先证明△DCE是等边三角形，进而可得∠AEB=60°，再根据∠A=∠AEB，可得△ABE是等腰三角形，进而可得△ABE是等边三角形．
证明：（1）∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠BCD=180°，
∵∠DCE+∠BCD=180°，
∴∠A=∠DCE，
∵DC=DE，
∴∠DCE=∠AEB，
∴∠A=∠AEB；
（2）∵∠A=∠AEB，
∴△ABE是等腰三角形，
∵EO⊥CD，
∴CF=DF，
∴EO是CD的垂直平分线，
∴ED=EC，
∵DC=DE，
∴DC=DE=EC，
∴△DCE是等边三角形，
∴∠AEB=60°，
∴△ABE是等边三角形．
17.【考点】三角形内角和定理，等腰三角形的性质，圆内接四边形的性质
【分析】(1）根据直角三角形的性质得到EF=BC，DF=BC，等量代换即可；
（2）根据三角形内角和定理和等腰三角形的性质计算；
（3）根据圆内接四边形的性质解答．
解：（1）△DEF是等腰三角形．
∵CE，BD分别是边AB，AC上的高，F是BC边上的中点，
∴EF=BC，DF=BC，
∴EF=DF，
∴△DEF是等腰三角形；
（2）∵FE=FB，FD=FC，
∴∠FEB=∠FBE，∠FDC=∠FCD，
∴∠FEB+∠FDC=∠FBE+∠FCD=180°﹣∠A=180°﹣x°，
∠AED+∠ADE=180°﹣∠A=180°﹣x°，
∴∠FED+∠FDE=360°﹣（180°﹣x°）﹣（180°﹣x°）=2x°，
∴∠EFD=180°﹣2x°；
（3）∠ABC=∠EDA．
∵∠BEC=∠BDC=90°，
∴B、E、D、C四点共圆，
∴∠ABC=∠EDA．
18.【考点】三角形内角和定理；圆内接四边形的性质．
【分析】（1）在△CDE与△CBF中，根据三角形内角和定理以及∠E=∠F，∠ECD=∠FCB，可得∠CDE=∠CBF，从而得∠ADC=∠ABC，由圆内接四边形定理可得∠ADC+∠ABC=180°，从而可得∠ADC=∠ABC=90°；
（2）由（1）可知∠ABC=90°，从而∠A=90°-∠E=48°；
（3）由四边形ABCD内接于⊙O，可得∠ADC+∠ABC=180°，从而得∠EDC+∠FBC=180°，在利用三角形内角和定理可得∠E+∠F+∠ECD+∠FCB=180°，从而得∠ECD+∠FCB=180°-（α+β），由周角可得∠BCD+∠FCE=180°+（α+β），从而可得∠BCD=90°+，从而得∠A=90°﹣．
解：（1）∠E=∠F，
∵∠DCE=∠BCF，
∴∠ADC=∠E+∠DCE，∠ABC=∠F+∠BCF，
∴∠ADC=∠ABC；
（2）由（1）知∠ADC=∠ABC，
∵∠EDC=∠ABC，
∴∠EDC=∠ADC，
∴∠ADC=90°，
∴∠A=90°﹣42°=48°；
（3）连结EF，如图，
∵四边形ABCD为圆的内接四边形，
∴∠ECD=∠A，
∵∠ECD=∠1+∠2，
∴∠A=∠1+∠2，
∵∠A+∠1+∠2+∠E+∠F=180°，
∴2∠A+α+β=180°，
∴∠A=90°﹣．