13.4课题学习最短路径问题课件(34张PPT)
文档属性
| 名称 | 13.4课题学习最短路径问题课件(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 772.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-16 14:31:27 | ||
图片预览






文档简介
l
八年级一班同学做游戏,在活动区域边缘放了一些球(如下图),小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
A
B小明
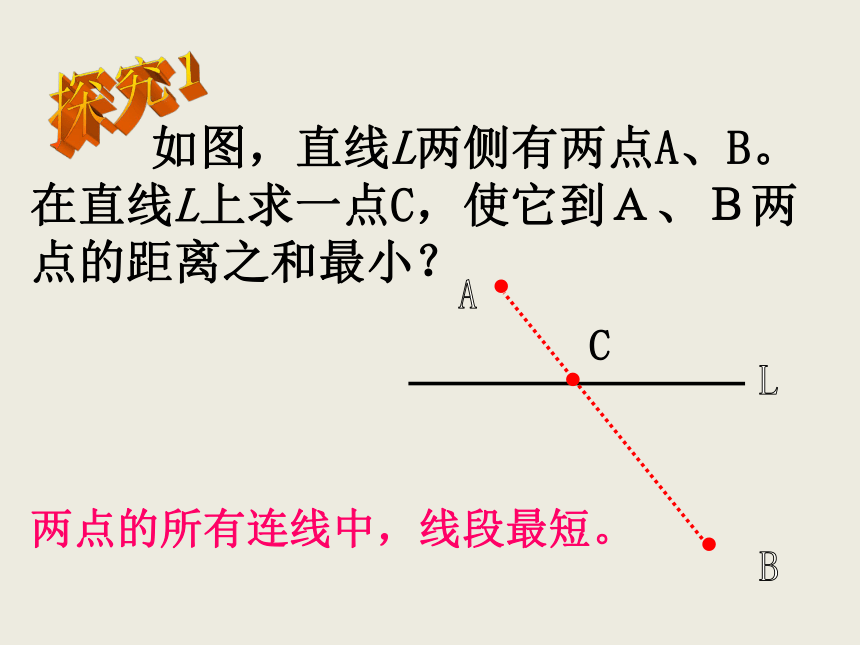
如图,直线L两侧有两点A、B。
在直线L上求一点C,使它到A、B两点的距离之和最小?
两点的所有连线中,线段最短。
C
A
B
C
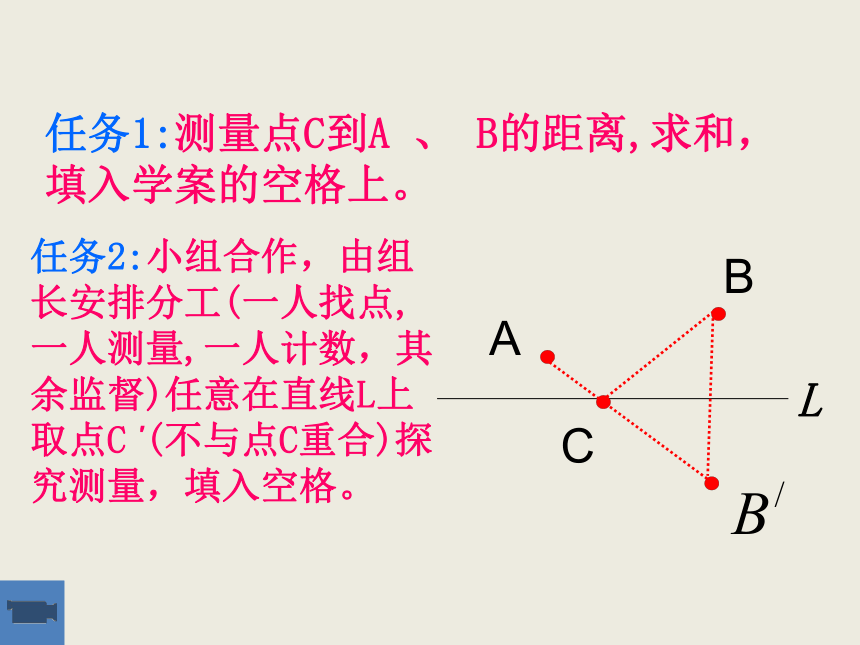
如图,直线L同侧有两点A、B。
在直线L上求一点C,使它到A、B两点的距离之和最小?
l
A
B
C
任务1:测量点C到A 、 B的距离,求和,填入学案的空格上。
任务2:小组合作,由组长安排分工(一人找点,一人测量,一人计数,其余监督)任意在直线L上取点C ′(不与点C重合)探究测量,填入空格。
L
A
B
C
l
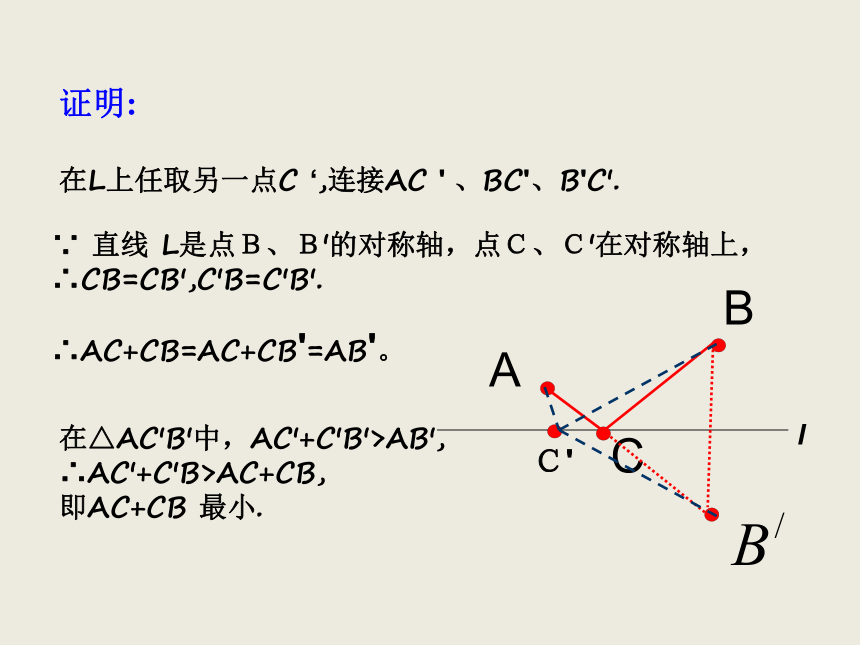
在L上任取另一点C ‘,连接AC ' 、BC'、B'C'.
∵ 直线 L是点B、B'的对称轴,点C、C'在对称轴上,
∴CB=CB',C'B=C'B'.
∴AC+CB=AC+CB'=AB'。
在△AC'B'中,AC'+C'B'>AB',
∴AC'+C'B>AC+CB,
即AC+CB 最小.
证明:
C'
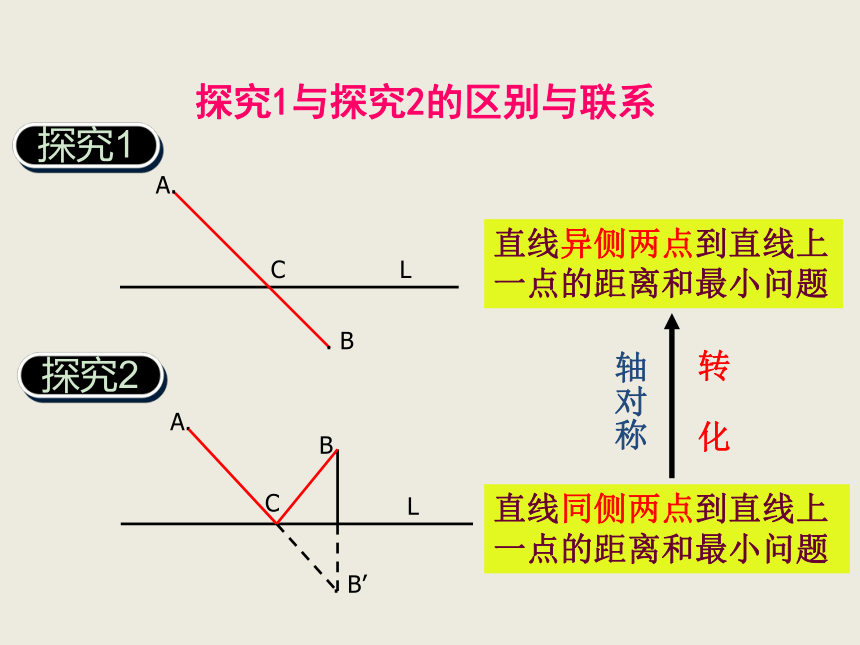
直线同侧两点到直线上一点的距离和最小问题
直线异侧两点到直线上一点的距离和最小问题
探究1与探究2的区别与联系
C
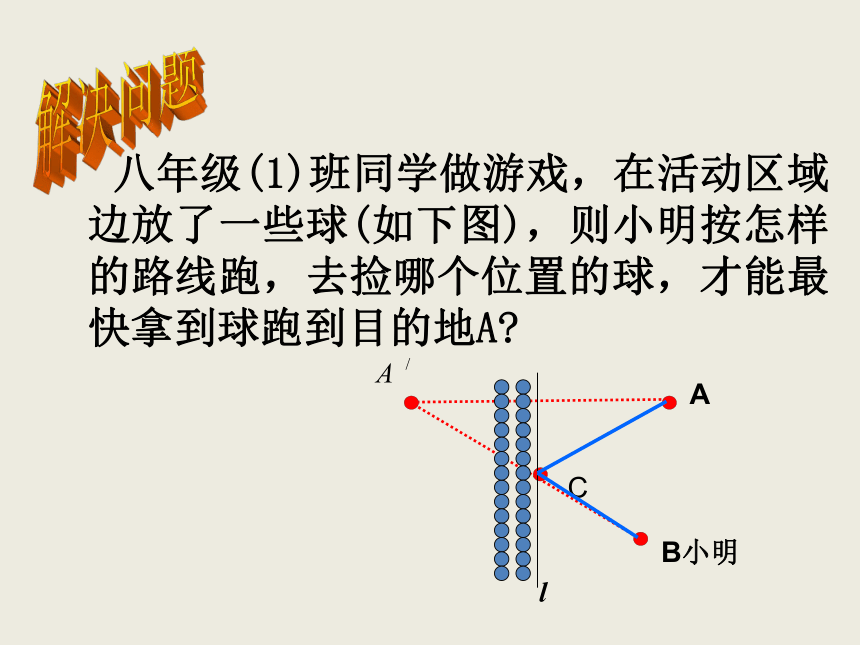
八年级(1)班同学做游戏,在活动区域边放了一些球(如下图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
A
B小明
l
巩固新知
∠AOB的边OA上有两点M、N,在∠AOB 的角平分线OC上找一点P,使MP+NP最小,下列作法正确的是()
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
P
P
P
P
N’
(A)
(D)
(C)
(B)
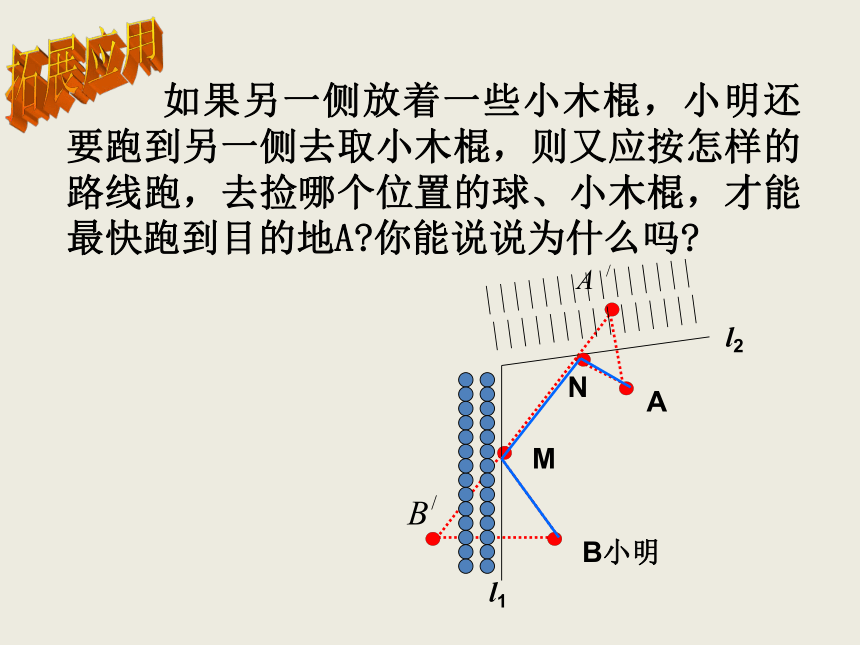
如果另一侧放着一些小木棍,小明还要跑到另一侧去取小木棍,则又应按怎样的路线跑,去捡哪个位置的球、小木棍,才能最快跑到目的地A?你能说说为什么吗?
M
N
A
B小明
l1
l2
要在燃气管道l上修建一个泵站,分别向A、B两镇供气.
(1)泵站修在管道的什么地方,可使它到A、B两镇的距离相等?
(2)泵站修在管道的什么地方,可使所用的输气管线最短?
A
B
l
造桥选址问题
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
思维分析
1、如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?
M
N
2、利用线段公理解决问题我们遇到了什么障碍呢?
我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图形变换能帮助我们呢?
思维火花
各抒己见
1、把A平移到岸边.
2、把B平移到岸边.
3、把桥平移到和A相连.
4、把桥平移到和B相连.
上述方法都能做到使AM+MN+BN不变吗?请检验.
合作与交流
1、2两种方法改变了.
怎样调整呢?
把A或B分别向下或上平移一个桥长
那么怎样确定桥的位置呢?
问题解决
A1
M
N
如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
理由;另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.
在△A1N1B中,由线段公理知A1N1+BN1>A1B
因此AM1+M1N1+BN1> AM+MN+BN
作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸与点M,
则点M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得BN∥EM且BN=EM,MN=CD,BD∥CE, BD=CE,
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC.CD.DB.CE,
则AB两地的距离为:
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN
所以桥的位置建在CD处,AB两地的路程最短。
A·
问题延伸一
如图,A和B两地之间有两条河,现要在两条河上各造一座桥MN和PQ.桥分别建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)
思维分析
如图,问题中所走总路径是AM+MN+NP+PQ+QB.
桥MN和PQ在中间,且方向不能改变,仍无法直接利用“两点之间,线段最短”解决问题,只有利用平移变换转移到两侧或同一侧先走桥长.
平移的方法有三种:两个桥长都平移到A点处、都平移到B点处、MN平移到A点处,PQ平移到B点处
思维方法一
1、沿垂直于第一条河岸的方向平移A点至AA1使AA1=MN,此时问题转化为问题基本题型两点(A1、B点)和一条河建桥(PQ)
2、利用基本问题的解决方法确定桥PQ:
(1)在沿垂直于第二条河岸的方向平移A1至A2,
使A1A2=PQ.
(2)连接A2B交A2的对岸Q点,在点处建桥PQ.
3、确定PQ的位置,也确定了BQ和PQ,此时问题可转化为由A点、P点和第一条河确定桥MN的位置.
连接A1P交A1的对岸于N点,在N点处建桥MN.
问题解决
沿垂直于河岸方向依次把A点A1、A2,使AA1=MN,A1A2 =PQ ;
连接A2B交于B点相邻河岸于Q点,建桥PQ;
连接A1P交A1的对岸于N点,建桥MN;
从A点到B点的最短路径为
AM+MN+NP+PQ+QB.
思维方法二
沿垂直于第一条河岸方向平移A点至A1 点,沿垂直于第二条河岸方向平移B点至B1点,连接A1B1 分别交A、B的对岸于N、P两点,建桥MN和PQ.
最短路径AM+MN+NP+PQ+QB转化为AA1+A1B1+BB1.
思维方法三
沿垂直于河岸方向依次把B点平移至B1、B2,使BB1=PQ,B1B2 =MN ;
连接B2A交于A点相邻河岸于M点,建桥MN;
连接B1N交B1的对岸于P点,建桥PQ;
从A点到B点的最短路径为AM+MN+NP+MN+NP+PQ+QB转化为AB2+B2B1+B1B.
问题延伸二
如图,A和B两地之间有三条河,现要在两条河上各造一座桥MN、PQ和GH.桥分别建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)
思维分析
如图,问题中所走总路径是AM+MN+NP+PQ+QG+GH+HB.
桥MN、PQ和GH在中间,且方向不能改变,仍无法直接利用“两点之间,线段最短”解决问题,只有利用平移变换转移到两侧或同一侧先走桥长.
平移的方法有四种:三个桥长都平移到A点处;都平移到B点处;MN、PQ平移到A点处;PQ、GH平移到B点处
问题解决
沿垂直于河岸方向依次把A点平移至A1、A2、A3,使AA1=MN,A1A2 =PQ,A2A3 =GH ;
连接A3B交于B点相邻河岸于H点,建桥GH;
连接A2G交第二河与G对岸的P点,建桥PQ;
连接A1P交第一条河与A的对岸于N点,建桥MN.
此时从A到B点路径最短.
沿垂直于河岸方向依次把A点平移至A1,使AA1=MN,平移B点至B1、B2 ,使BB1=GH,B1B2 =PQ ;
连接A1B2交第一条河与A点相对河岸于N点,交第二条河与N相邻河岸于P点,建桥MN、PQ;
连接B1Q交第三条河与Q相邻河岸的G点,建桥GH;
此时从A到B点路径最短.
问题解决
沿垂直于河岸方向依次把A点平移至A1、A2,使AA1=MN,A1A2=PQ,平移B点至B1 ,使BB1=GH ;
连接A2B1交第三条河与B点相对河岸于G点,交第二条河与G相邻河岸于Q点,建桥GH、PQ;
连接A1P交第一条河与P相邻河岸的N点,建桥MN;
此时从A到B点路径最短.
问题解决
延伸小结
同样,当A、B两点之间有4、5、6,...n条河时,我们仍可以利用平移转化桥长来解决问题.
例如: 沿垂直于河岸方向平移A点依次至A1、A2、A3 ,...,An,平移距离分别等于各自河宽,AnB交第n条河近B点河岸于Nn,建桥MnNn,连接MnAn-1交第(n-1)条河近B点河岸与Nn-1,建桥Mn-1Nn-1,...,连接M1A交第一条河近B点河岸于N1,建桥M1N1,此时所走路径最短.
通过这节课的学习说说你的收获:
课本P93复习题第15题。
作 业
八年级一班同学做游戏,在活动区域边缘放了一些球(如下图),小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
A
B小明
如图,直线L两侧有两点A、B。
在直线L上求一点C,使它到A、B两点的距离之和最小?
两点的所有连线中,线段最短。
C
A
B
C
如图,直线L同侧有两点A、B。
在直线L上求一点C,使它到A、B两点的距离之和最小?
l
A
B
C
任务1:测量点C到A 、 B的距离,求和,填入学案的空格上。
任务2:小组合作,由组长安排分工(一人找点,一人测量,一人计数,其余监督)任意在直线L上取点C ′(不与点C重合)探究测量,填入空格。
L
A
B
C
l
在L上任取另一点C ‘,连接AC ' 、BC'、B'C'.
∵ 直线 L是点B、B'的对称轴,点C、C'在对称轴上,
∴CB=CB',C'B=C'B'.
∴AC+CB=AC+CB'=AB'。
在△AC'B'中,AC'+C'B'>AB',
∴AC'+C'B>AC+CB,
即AC+CB 最小.
证明:
C'
直线同侧两点到直线上一点的距离和最小问题
直线异侧两点到直线上一点的距离和最小问题
探究1与探究2的区别与联系
C
八年级(1)班同学做游戏,在活动区域边放了一些球(如下图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
A
B小明
l
巩固新知
∠AOB的边OA上有两点M、N,在∠AOB 的角平分线OC上找一点P,使MP+NP最小,下列作法正确的是()
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
P
P
P
P
N’
(A)
(D)
(C)
(B)
如果另一侧放着一些小木棍,小明还要跑到另一侧去取小木棍,则又应按怎样的路线跑,去捡哪个位置的球、小木棍,才能最快跑到目的地A?你能说说为什么吗?
M
N
A
B小明
l1
l2
要在燃气管道l上修建一个泵站,分别向A、B两镇供气.
(1)泵站修在管道的什么地方,可使它到A、B两镇的距离相等?
(2)泵站修在管道的什么地方,可使所用的输气管线最短?
A
B
l
造桥选址问题
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
思维分析
1、如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?
M
N
2、利用线段公理解决问题我们遇到了什么障碍呢?
我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图形变换能帮助我们呢?
思维火花
各抒己见
1、把A平移到岸边.
2、把B平移到岸边.
3、把桥平移到和A相连.
4、把桥平移到和B相连.
上述方法都能做到使AM+MN+BN不变吗?请检验.
合作与交流
1、2两种方法改变了.
怎样调整呢?
把A或B分别向下或上平移一个桥长
那么怎样确定桥的位置呢?
问题解决
A1
M
N
如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
理由;另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.
在△A1N1B中,由线段公理知A1N1+BN1>A1B
因此AM1+M1N1+BN1> AM+MN+BN
作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸与点M,
则点M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得BN∥EM且BN=EM,MN=CD,BD∥CE, BD=CE,
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC.CD.DB.CE,
则AB两地的距离为:
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN
所以桥的位置建在CD处,AB两地的路程最短。
A·
问题延伸一
如图,A和B两地之间有两条河,现要在两条河上各造一座桥MN和PQ.桥分别建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)
思维分析
如图,问题中所走总路径是AM+MN+NP+PQ+QB.
桥MN和PQ在中间,且方向不能改变,仍无法直接利用“两点之间,线段最短”解决问题,只有利用平移变换转移到两侧或同一侧先走桥长.
平移的方法有三种:两个桥长都平移到A点处、都平移到B点处、MN平移到A点处,PQ平移到B点处
思维方法一
1、沿垂直于第一条河岸的方向平移A点至AA1使AA1=MN,此时问题转化为问题基本题型两点(A1、B点)和一条河建桥(PQ)
2、利用基本问题的解决方法确定桥PQ:
(1)在沿垂直于第二条河岸的方向平移A1至A2,
使A1A2=PQ.
(2)连接A2B交A2的对岸Q点,在点处建桥PQ.
3、确定PQ的位置,也确定了BQ和PQ,此时问题可转化为由A点、P点和第一条河确定桥MN的位置.
连接A1P交A1的对岸于N点,在N点处建桥MN.
问题解决
沿垂直于河岸方向依次把A点A1、A2,使AA1=MN,A1A2 =PQ ;
连接A2B交于B点相邻河岸于Q点,建桥PQ;
连接A1P交A1的对岸于N点,建桥MN;
从A点到B点的最短路径为
AM+MN+NP+PQ+QB.
思维方法二
沿垂直于第一条河岸方向平移A点至A1 点,沿垂直于第二条河岸方向平移B点至B1点,连接A1B1 分别交A、B的对岸于N、P两点,建桥MN和PQ.
最短路径AM+MN+NP+PQ+QB转化为AA1+A1B1+BB1.
思维方法三
沿垂直于河岸方向依次把B点平移至B1、B2,使BB1=PQ,B1B2 =MN ;
连接B2A交于A点相邻河岸于M点,建桥MN;
连接B1N交B1的对岸于P点,建桥PQ;
从A点到B点的最短路径为AM+MN+NP+MN+NP+PQ+QB转化为AB2+B2B1+B1B.
问题延伸二
如图,A和B两地之间有三条河,现要在两条河上各造一座桥MN、PQ和GH.桥分别建在何处才能使从A到B的路径最短?(假定河的两岸是平行的直线,桥要与河岸垂直)
思维分析
如图,问题中所走总路径是AM+MN+NP+PQ+QG+GH+HB.
桥MN、PQ和GH在中间,且方向不能改变,仍无法直接利用“两点之间,线段最短”解决问题,只有利用平移变换转移到两侧或同一侧先走桥长.
平移的方法有四种:三个桥长都平移到A点处;都平移到B点处;MN、PQ平移到A点处;PQ、GH平移到B点处
问题解决
沿垂直于河岸方向依次把A点平移至A1、A2、A3,使AA1=MN,A1A2 =PQ,A2A3 =GH ;
连接A3B交于B点相邻河岸于H点,建桥GH;
连接A2G交第二河与G对岸的P点,建桥PQ;
连接A1P交第一条河与A的对岸于N点,建桥MN.
此时从A到B点路径最短.
沿垂直于河岸方向依次把A点平移至A1,使AA1=MN,平移B点至B1、B2 ,使BB1=GH,B1B2 =PQ ;
连接A1B2交第一条河与A点相对河岸于N点,交第二条河与N相邻河岸于P点,建桥MN、PQ;
连接B1Q交第三条河与Q相邻河岸的G点,建桥GH;
此时从A到B点路径最短.
问题解决
沿垂直于河岸方向依次把A点平移至A1、A2,使AA1=MN,A1A2=PQ,平移B点至B1 ,使BB1=GH ;
连接A2B1交第三条河与B点相对河岸于G点,交第二条河与G相邻河岸于Q点,建桥GH、PQ;
连接A1P交第一条河与P相邻河岸的N点,建桥MN;
此时从A到B点路径最短.
问题解决
延伸小结
同样,当A、B两点之间有4、5、6,...n条河时,我们仍可以利用平移转化桥长来解决问题.
例如: 沿垂直于河岸方向平移A点依次至A1、A2、A3 ,...,An,平移距离分别等于各自河宽,AnB交第n条河近B点河岸于Nn,建桥MnNn,连接MnAn-1交第(n-1)条河近B点河岸与Nn-1,建桥Mn-1Nn-1,...,连接M1A交第一条河近B点河岸于N1,建桥M1N1,此时所走路径最短.
通过这节课的学习说说你的收获:
课本P93复习题第15题。
作 业
