24.2.2 直线和圆的位置关系课时作业(5)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系课时作业(5) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-17 10:49:35 | ||
图片预览



文档简介
24.2.2 直线和圆的位置关系课时作业(5)
姓名:__________班级:__________考号:__________
一、选择题
1.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
2.如图,⊙O 是△ABC 的内切圆,切点分别是 D、E、F.已知∠A=100°,∠C=40°,则∠DFE 的 度数是( )
A.55° B.60° C.65° D.70°
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
4.如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A.240° B.360° C.480° D.540°
5.已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )
A. B. C. D.
6.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
7.如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
A.2 B.3 C. D.
8.如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心 B.点O是△ABC的外心
C.△ABC是正三角形 D.△ABC是等腰三角形
二、填空题
9.直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .
10.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.
11.在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为
12.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .
13.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为______.
14.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
三、解答题
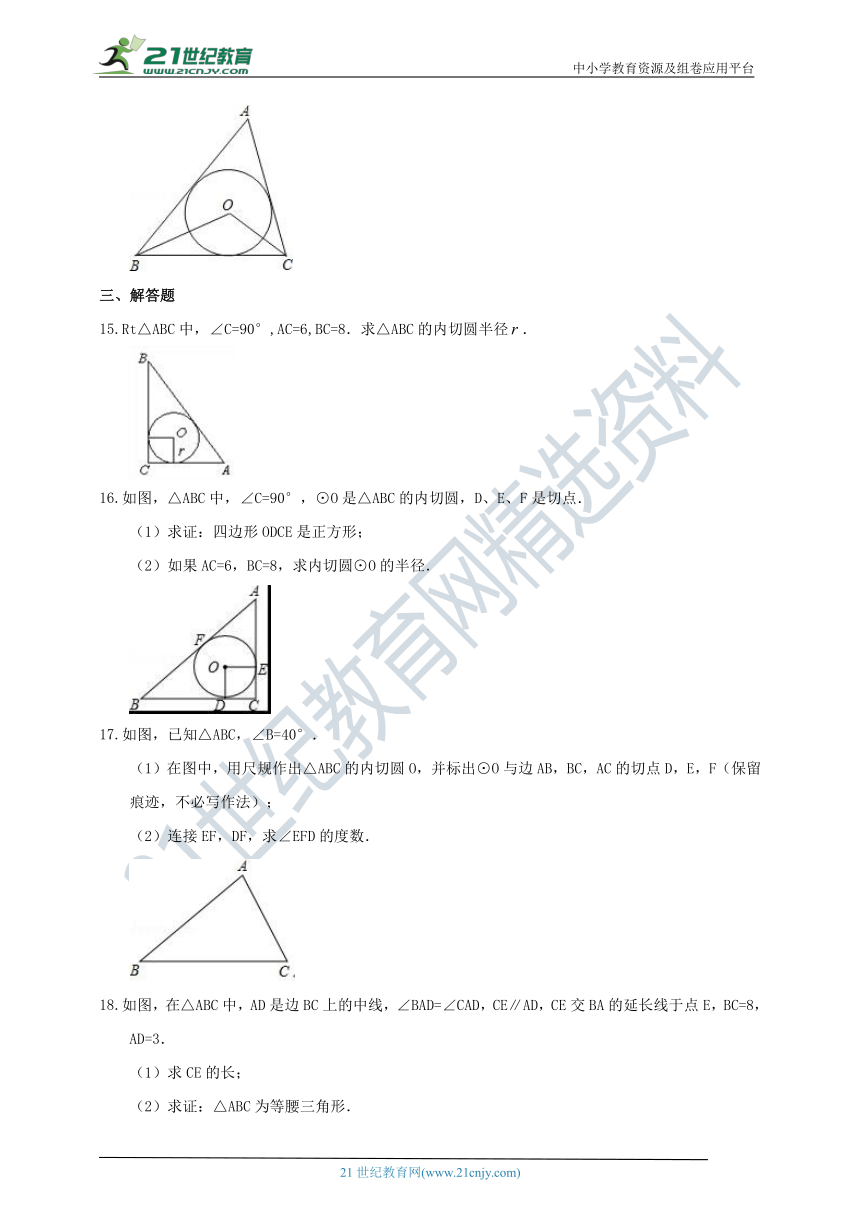
15.Rt△ABC中,∠C=90°,AC=6,BC=8.求△ABC的内切圆半径.
16.如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果AC=6,BC=8,求内切圆⊙O的半径.
17.如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
18.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
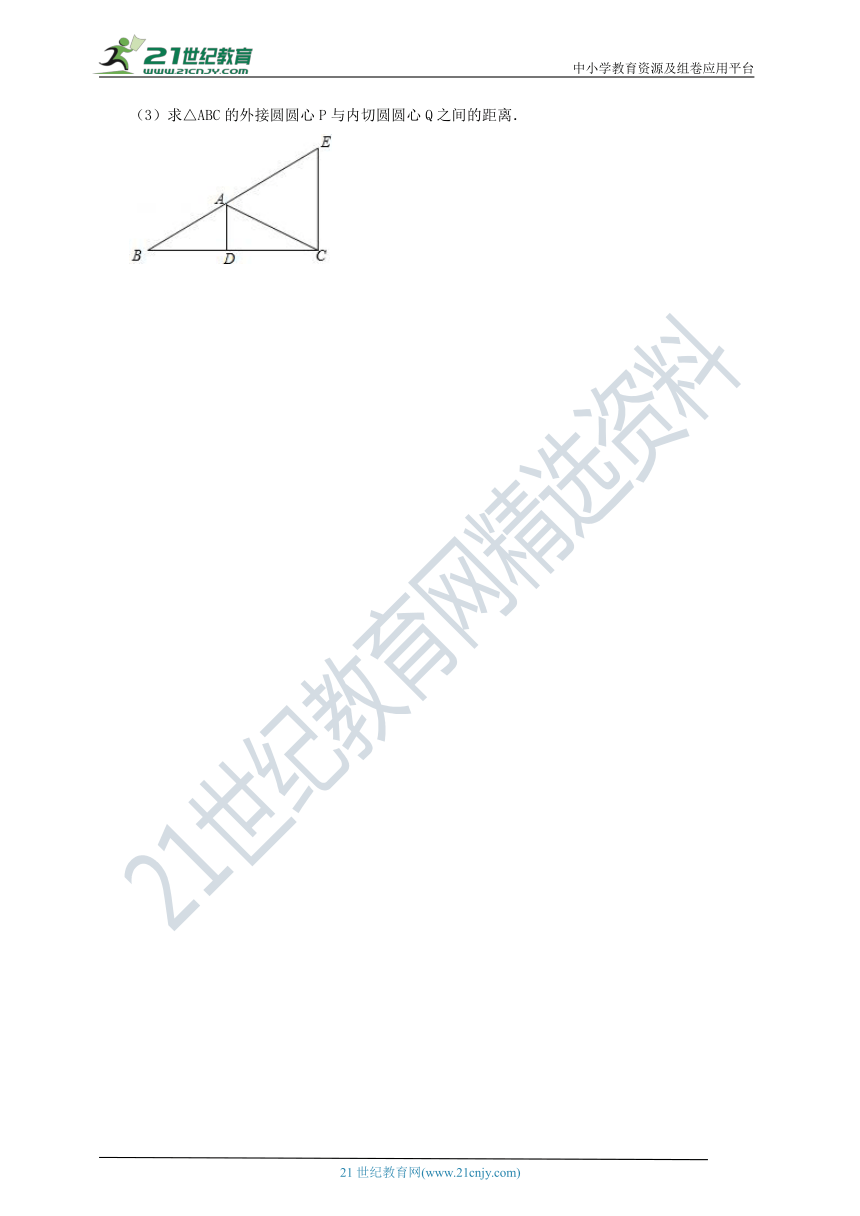
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
答案解析
一 、选择题
1.【考点】三角形的内切圆与内心;勾股定理;三角形的外接圆与外心.
【分析】直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r=;外接圆的半径就是斜边的一半.
解:∵AB=5,AC=3,
∴BC==4,
∴外接圆半径==2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径==1.
故选C.
【点评】解决此题的关键是熟练掌握直角三角形的三边与外接圆半径,内切圆半径之间的关系.
2.【考点】三角形的内切圆与内心.
【分析】根据三角形的内角和定理求得∠B=40°,再根据切线的性质以及四边形的内角和定理得出
∠DOE=140°,再根据圆周角定理即可得出∠DFE=70°.
解:∵∠A=100°,∠C=40°,
∴∠B=180°﹣∠A﹣∠C=40°,
∵⊙O 是△ABC 的内切圆,切点分别是 D、E、F,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°﹣∠B=140°,
∴∠DFE= ∠DOE=70°.
故选:D.
【点评】本题考查了三角形的内切圆、切线的性质、圆周角定理、四边形内角和定理;熟练掌握切 线的性质,求出∠DOE 是解决问题的关键.
3.【考点】三角形的内切圆与内心.
【分析】根据三角形的内切圆得出点O到三边的距离相等,即可得出结论.
解:∵⊙O是△ABC的内切圆,
则点O到三边的距离相等,
∴点O是△ABC的三条角平分线的交点;
故选:B.
4.【考点】三角形的内切圆与内心;等边三角形的性质;旋转的性质.
【分析】根据正三角形的性质分别得出点O转动的角度,进而得出答案.
解:由题意可得:第一次AO顺时针转动了120°,第二次AO顺时针转动了240°,第三次AO顺时针转动了120°,
故当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是:120°+240°+120°=480°.
故选:C.
5.【考点】三角形的内切圆与内心.
【分析】如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.由AD2=AB2﹣BD2=AC2﹣CD2,可得72﹣x2=82﹣(5﹣x)2,解得x=1,推出AD=4,由?BC?AD=(AB+BC+AC)?r,列出方程即可解决问题.
解:如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.
由勾股定理可知:AD2=AB2﹣BD2=AC2﹣CD2,
即72﹣x2=82﹣(5﹣x)2,解得x=1,
∴AD=4,
∵?BC?AD=(AB+BC+AC)?r,
×5×4=×20×r,
∴r=,
故选C
6.【考点】三角形的内切圆与内心
【分析】由点I是△ABC的内心知∠BAC=2∠IAC、∠ACB=2∠ICA,从而求得∠B=180°﹣(∠BAC+∠ACB)=180°﹣2(180°﹣∠AIC),再利用圆内接四边形的外角等于内对角可得答案.
解:∵点I是△ABC的内心,
∴∠BAC=2∠IAC、∠ACB=2∠ICA,
∵∠AIC=124°,
∴∠B=180°﹣(∠BAC+∠ACB)
=180°﹣2(∠IAC+∠ICA)
=180°﹣2(180°﹣∠AIC)
=68°,
又四边形ABCD内接于⊙O,
∴∠CDE=∠B=68°,
故选:C.
【点评】本题主要考查三角形的内切圆与内心,解题的关键是掌握三角形的内心的性质及圆内接四边形的性质.
7.【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【分析】过点P作PD⊥AC,PE⊥BC,PF⊥AB,由点P是内切圆的圆心可知PD=PE=PF,再由切线长定理可知CD=CE,BE=BF,故可得出四边形PDCE是正方形,再由勾股定理求出AB的长,故可得出PD的长,由BE=BC﹣CE可得出BE的长,根据点O为直角三角形的外心可得出OB的长,进而得出OF的长,根据勾股定理即可得出结论.
解:过点P作PD⊥AC,PE⊥BC,PF⊥AB,
∵点P是内切圆的圆心,
∴PD=PE=PF,CD=CE,BE=BF
∴四边形PDCE是正方形.
∵△ABC中,∠C=90°,BC=6,AC=8,
∴AB==10,
∴PE=PF=PE==2,
∴BE=BF=6﹣2=4.
∵点O为△ABC的外心,
∴OB=AB=5,
∴OF=OB﹣BF=5﹣4=1,
∴OP===.
故选C.
【点评】本题考查的是三角形的内切圆与内心,熟知直角三角形的内心与外心的求法是解答此题的关键.
8.【考点】三角形的内切圆与内心.
【分析】过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,根据垂径定理和已知求出DM=KQ=FN,根据勾股定理求出OM=ON=OQ,根据三角形内心的定义求出即可.
解:
过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
故选A.
【点评】本题考查了垂径定理,勾股定理,三角形的内心的应用,注意:三角形的内心到三角形三边的距离相等.
二 、填空题
9.【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【分析】首先根据勾股定理求得该直角三角形的斜边是5,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解:∵直角三角形两直角边为3,4,
∴斜边长==5,
∴外接圆半径==2.5,内切圆半径==1,
∴外接圆和内切圆半径之和=2.5+1=3.5.
故答案为:3.5.
10.【考点】 三角形的内切圆与内心;等腰三角形的性质.
【分析】如图,设△ABC的内切圆半径为r,由勾股定理得AD=12,再由切线长定理得AE=8,根据勾股定理求得r即可.
解:如图,∵AB=AC=13cm,BC=10cm,
∴BD=5cm,
∴AD=12cm,
根据切线长定理,AE=AB﹣BE=AB﹣BD=13﹣5=8,
设△ABC的内切圆半径为r,
∴AO=12﹣r,
∴(12﹣r)2﹣r2=64,
解得r=,
故答案为.
【点评】本题考查了勾股定理、三角形的内切圆和等腰三角形的性质,是基础知识要熟练掌握.
11.【考点】勾股定理;三角形的内切圆与内心
【分析】先利用勾股定理计算出AB的长,再利用直角三角形内切圆的半径的计算方法求出△ABC的内切圆的半径,然后利用圆的面积公式求解.
解:∵∠C=90°,CA=8,CB=6,
∴AB==10,
∴△ABC的内切圆的半径==2,
∴△ABC内切圆的周长=π?22=4π.
故答案为4π.
【点评】本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.记住直角三角形内切圆半径的计算方法.
12.【考点】勾股定理,三角形的内切圆
【分析】先利用勾股定理计算出BC=8,然后利用直角三角形内切圆的半径=(a、b为直角边,c为斜边)进行计算.
解:∵∠C=90°,AB=10,AC=6,
∴BC==8,
∴这个三角形的内切圆半径==2.
故答案为2.
13.【考点】三角形的内切圆与内心;圆周角定理.
【分析】根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=÷2=58°,
∴∠BEC=180°﹣58°=122°.
故答案为:122°.
14.【考点】三角形的内切圆与内心.
【分析】由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线;再利用角平分线的定义可知∠OBC+∠OCB=(∠ABC+∠ACB),代入数值即可求∠BOC=115°.
解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°﹣65°=115°.
【点评】本题通过三角形内切圆,考查切线的性质.
三 、解答题
15.【考点】切线长定理,三角形的内切圆半径
【分析】设AB、BC、AC与⊙O的切点分别为D、E、F;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF= (AC+BC-AB),由此可求出r的长.
解:如图,
在Rt△ABC,∠C=90°,AC=6,BC=8,∴AB==10,
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=(AC+BC-AB),
即:r=(6+8-10)=2.
【点睛】本题主要考查了切线长定理以及三角形的内切圆半径,能结合图形选择恰当的方法是解题的关键.
16.【考点】正方形的判定,三角形的内切圆与内心,勾股定理,切线长定理
【分析】(1)根据三角形内切圆的性质可得OE⊥AC,OD⊥BC,OE=OD,据此可证明四边形ODCE是正方形;
(2)先根据勾股定理求出AB的长;接下来利用由切线长定理得,AF=AE,BD=BF,CD=CE,由CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB即可求出⊙O的半径为2.
解:方形的判定,三角形的内切圆与内心,勾股定理,切线长定理
(1)∵⊙O是△ABC的内切圆,
∴OD⊥BC,OE⊥AC,又∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形;
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
由切线长定理得,AF=AE,BD=BF,CD=CE,
∴CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB=4,
则CE=2,即⊙O的半径为2.
【点睛】本题主要考查对正方形的判定,三角形的内切圆与内心,勾股定理,切线长定理等知识点的理解和掌握,能熟练地运用这些性质进行推理和计算是解此题的关键.
17.【考点】作图—复杂作图;三角形的内切圆与内心.
【分析】(1)直接利用基本作图即可得出结论;
(2)利用四边形的性质,三角形的内切圆的性质即可得出结论.
解:(1)如图1,
⊙O即为所求.
(2)如图2,
连接OD,OE,
∴OD⊥AB,OE⊥BC,
∴∠ODB=∠OEB=90°,
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD=70°.
18.【考点】平行线的性质;等腰三角形的判定与性质;三角形的外接圆与外心;三角形的内切圆与内心
【分析】(1)证明AD为△BCE的中位线得到CE=2AD=6;
(2)通过证明AC=AE得到AB=AC;
(3)如图,连接BP、BQ、CQ,先利用勾股定理计算出AB=5,设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中利用勾股定理得到(R﹣3)2+42=R2,解得R=,则PD=,再利用面积法求出r=,即QD=,然后计算PD+QD即可.
(1)解:∵AD是边BC上的中线,
∴BD=CD,
∵CE∥AD,
∴AD为△BCE的中位线,
∴CE=2AD=6;
(2)证明:∵CE∥AD,
∴∠BAD=∠E,∠CAD=∠ACE,
而∠BAD=∠CAD,
∴∠ACE=∠E,
∴AE=AC,
而AB=AE,
∴AB=AC,
∴△ABC为等腰三角形.
(3)如图,连接BP、BQ、CQ,
在Rt△ABD中,AB==5,
设⊙P的半径为R,⊙Q的半径为r,
在Rt△PBD中,(R﹣3)2+42=R2,解得R=,
∴PD=PA﹣AD=﹣3=,
∵S△ABQ+S△BCQ+S△ACQ=S△ABC,
∴?r?5+?r?8+?r?5=?3?8,解得r=,
即QD=,
∴PQ=PD+QD=+=.
答:△ABC的外接圆圆心P与内切圆圆心Q之间的距离为.
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等腰三角形的判定与性质和三角形的外接圆.
姓名:__________班级:__________考号:__________
一、选择题
1.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
2.如图,⊙O 是△ABC 的内切圆,切点分别是 D、E、F.已知∠A=100°,∠C=40°,则∠DFE 的 度数是( )
A.55° B.60° C.65° D.70°
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
4.如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A.240° B.360° C.480° D.540°
5.已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )
A. B. C. D.
6.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
7.如图,△ABC中,∠C=90°,⊙P为△ABC的内切圆,点O为△ABC的外心,BC=6,AC=8,则OP的长为( )
A.2 B.3 C. D.
8.如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心 B.点O是△ABC的外心
C.△ABC是正三角形 D.△ABC是等腰三角形
二、填空题
9.直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .
10.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.
11.在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为
12.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为 .
13.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为______.
14.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.
三、解答题
15.Rt△ABC中,∠C=90°,AC=6,BC=8.求△ABC的内切圆半径.
16.如图,△ABC中,∠C=90°,⊙O是△ABC的内切圆,D、E、F是切点.
(1)求证:四边形ODCE是正方形;
(2)如果AC=6,BC=8,求内切圆⊙O的半径.
17.如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
18.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
答案解析
一 、选择题
1.【考点】三角形的内切圆与内心;勾股定理;三角形的外接圆与外心.
【分析】直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r=;外接圆的半径就是斜边的一半.
解:∵AB=5,AC=3,
∴BC==4,
∴外接圆半径==2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径==1.
故选C.
【点评】解决此题的关键是熟练掌握直角三角形的三边与外接圆半径,内切圆半径之间的关系.
2.【考点】三角形的内切圆与内心.
【分析】根据三角形的内角和定理求得∠B=40°,再根据切线的性质以及四边形的内角和定理得出
∠DOE=140°,再根据圆周角定理即可得出∠DFE=70°.
解:∵∠A=100°,∠C=40°,
∴∠B=180°﹣∠A﹣∠C=40°,
∵⊙O 是△ABC 的内切圆,切点分别是 D、E、F,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°﹣∠B=140°,
∴∠DFE= ∠DOE=70°.
故选:D.
【点评】本题考查了三角形的内切圆、切线的性质、圆周角定理、四边形内角和定理;熟练掌握切 线的性质,求出∠DOE 是解决问题的关键.
3.【考点】三角形的内切圆与内心.
【分析】根据三角形的内切圆得出点O到三边的距离相等,即可得出结论.
解:∵⊙O是△ABC的内切圆,
则点O到三边的距离相等,
∴点O是△ABC的三条角平分线的交点;
故选:B.
4.【考点】三角形的内切圆与内心;等边三角形的性质;旋转的性质.
【分析】根据正三角形的性质分别得出点O转动的角度,进而得出答案.
解:由题意可得:第一次AO顺时针转动了120°,第二次AO顺时针转动了240°,第三次AO顺时针转动了120°,
故当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是:120°+240°+120°=480°.
故选:C.
5.【考点】三角形的内切圆与内心.
【分析】如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.由AD2=AB2﹣BD2=AC2﹣CD2,可得72﹣x2=82﹣(5﹣x)2,解得x=1,推出AD=4,由?BC?AD=(AB+BC+AC)?r,列出方程即可解决问题.
解:如图,AB=7,BC=5,AC=8,内切圆的半径为r,切点为G、E、F,作AD⊥BC于D,设BD=x,则CD=5﹣x.
由勾股定理可知:AD2=AB2﹣BD2=AC2﹣CD2,
即72﹣x2=82﹣(5﹣x)2,解得x=1,
∴AD=4,
∵?BC?AD=(AB+BC+AC)?r,
×5×4=×20×r,
∴r=,
故选C
6.【考点】三角形的内切圆与内心
【分析】由点I是△ABC的内心知∠BAC=2∠IAC、∠ACB=2∠ICA,从而求得∠B=180°﹣(∠BAC+∠ACB)=180°﹣2(180°﹣∠AIC),再利用圆内接四边形的外角等于内对角可得答案.
解:∵点I是△ABC的内心,
∴∠BAC=2∠IAC、∠ACB=2∠ICA,
∵∠AIC=124°,
∴∠B=180°﹣(∠BAC+∠ACB)
=180°﹣2(∠IAC+∠ICA)
=180°﹣2(180°﹣∠AIC)
=68°,
又四边形ABCD内接于⊙O,
∴∠CDE=∠B=68°,
故选:C.
【点评】本题主要考查三角形的内切圆与内心,解题的关键是掌握三角形的内心的性质及圆内接四边形的性质.
7.【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【分析】过点P作PD⊥AC,PE⊥BC,PF⊥AB,由点P是内切圆的圆心可知PD=PE=PF,再由切线长定理可知CD=CE,BE=BF,故可得出四边形PDCE是正方形,再由勾股定理求出AB的长,故可得出PD的长,由BE=BC﹣CE可得出BE的长,根据点O为直角三角形的外心可得出OB的长,进而得出OF的长,根据勾股定理即可得出结论.
解:过点P作PD⊥AC,PE⊥BC,PF⊥AB,
∵点P是内切圆的圆心,
∴PD=PE=PF,CD=CE,BE=BF
∴四边形PDCE是正方形.
∵△ABC中,∠C=90°,BC=6,AC=8,
∴AB==10,
∴PE=PF=PE==2,
∴BE=BF=6﹣2=4.
∵点O为△ABC的外心,
∴OB=AB=5,
∴OF=OB﹣BF=5﹣4=1,
∴OP===.
故选C.
【点评】本题考查的是三角形的内切圆与内心,熟知直角三角形的内心与外心的求法是解答此题的关键.
8.【考点】三角形的内切圆与内心.
【分析】过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,根据垂径定理和已知求出DM=KQ=FN,根据勾股定理求出OM=ON=OQ,根据三角形内心的定义求出即可.
解:
过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,
由垂径定理得:DM=DE,KQ=KH,FN=FG,
∵DE=FG=HK,
∴DM=KQ=FN,
∵OD=OK=OF,
∴由勾股定理得:OM=ON=OQ,
即O到三角形ABC三边的距离相等,
∴O是△ABC的内心,
故选A.
【点评】本题考查了垂径定理,勾股定理,三角形的内心的应用,注意:三角形的内心到三角形三边的距离相等.
二 、填空题
9.【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【分析】首先根据勾股定理求得该直角三角形的斜边是5,再根据其外接圆的半径等于斜边的一半和内切圆的半径等于两条直角边的和与斜边的差的一半进行计算.
解:∵直角三角形两直角边为3,4,
∴斜边长==5,
∴外接圆半径==2.5,内切圆半径==1,
∴外接圆和内切圆半径之和=2.5+1=3.5.
故答案为:3.5.
10.【考点】 三角形的内切圆与内心;等腰三角形的性质.
【分析】如图,设△ABC的内切圆半径为r,由勾股定理得AD=12,再由切线长定理得AE=8,根据勾股定理求得r即可.
解:如图,∵AB=AC=13cm,BC=10cm,
∴BD=5cm,
∴AD=12cm,
根据切线长定理,AE=AB﹣BE=AB﹣BD=13﹣5=8,
设△ABC的内切圆半径为r,
∴AO=12﹣r,
∴(12﹣r)2﹣r2=64,
解得r=,
故答案为.
【点评】本题考查了勾股定理、三角形的内切圆和等腰三角形的性质,是基础知识要熟练掌握.
11.【考点】勾股定理;三角形的内切圆与内心
【分析】先利用勾股定理计算出AB的长,再利用直角三角形内切圆的半径的计算方法求出△ABC的内切圆的半径,然后利用圆的面积公式求解.
解:∵∠C=90°,CA=8,CB=6,
∴AB==10,
∴△ABC的内切圆的半径==2,
∴△ABC内切圆的周长=π?22=4π.
故答案为4π.
【点评】本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.记住直角三角形内切圆半径的计算方法.
12.【考点】勾股定理,三角形的内切圆
【分析】先利用勾股定理计算出BC=8,然后利用直角三角形内切圆的半径=(a、b为直角边,c为斜边)进行计算.
解:∵∠C=90°,AB=10,AC=6,
∴BC==8,
∴这个三角形的内切圆半径==2.
故答案为2.
13.【考点】三角形的内切圆与内心;圆周角定理.
【分析】根据圆周角定理可求∠CAD=32°,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=÷2=58°,
∴∠BEC=180°﹣58°=122°.
故答案为:122°.
14.【考点】三角形的内切圆与内心.
【分析】由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线;再利用角平分线的定义可知∠OBC+∠OCB=(∠ABC+∠ACB),代入数值即可求∠BOC=115°.
解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°﹣65°=115°.
【点评】本题通过三角形内切圆,考查切线的性质.
三 、解答题
15.【考点】切线长定理,三角形的内切圆半径
【分析】设AB、BC、AC与⊙O的切点分别为D、E、F;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF= (AC+BC-AB),由此可求出r的长.
解:如图,
在Rt△ABC,∠C=90°,AC=6,BC=8,∴AB==10,
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=(AC+BC-AB),
即:r=(6+8-10)=2.
【点睛】本题主要考查了切线长定理以及三角形的内切圆半径,能结合图形选择恰当的方法是解题的关键.
16.【考点】正方形的判定,三角形的内切圆与内心,勾股定理,切线长定理
【分析】(1)根据三角形内切圆的性质可得OE⊥AC,OD⊥BC,OE=OD,据此可证明四边形ODCE是正方形;
(2)先根据勾股定理求出AB的长;接下来利用由切线长定理得,AF=AE,BD=BF,CD=CE,由CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB即可求出⊙O的半径为2.
解:方形的判定,三角形的内切圆与内心,勾股定理,切线长定理
(1)∵⊙O是△ABC的内切圆,
∴OD⊥BC,OE⊥AC,又∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形;
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
由切线长定理得,AF=AE,BD=BF,CD=CE,
∴CD+CE=BC+AC﹣BD﹣AE=BC+AC﹣AB=4,
则CE=2,即⊙O的半径为2.
【点睛】本题主要考查对正方形的判定,三角形的内切圆与内心,勾股定理,切线长定理等知识点的理解和掌握,能熟练地运用这些性质进行推理和计算是解此题的关键.
17.【考点】作图—复杂作图;三角形的内切圆与内心.
【分析】(1)直接利用基本作图即可得出结论;
(2)利用四边形的性质,三角形的内切圆的性质即可得出结论.
解:(1)如图1,
⊙O即为所求.
(2)如图2,
连接OD,OE,
∴OD⊥AB,OE⊥BC,
∴∠ODB=∠OEB=90°,
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD=70°.
18.【考点】平行线的性质;等腰三角形的判定与性质;三角形的外接圆与外心;三角形的内切圆与内心
【分析】(1)证明AD为△BCE的中位线得到CE=2AD=6;
(2)通过证明AC=AE得到AB=AC;
(3)如图,连接BP、BQ、CQ,先利用勾股定理计算出AB=5,设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中利用勾股定理得到(R﹣3)2+42=R2,解得R=,则PD=,再利用面积法求出r=,即QD=,然后计算PD+QD即可.
(1)解:∵AD是边BC上的中线,
∴BD=CD,
∵CE∥AD,
∴AD为△BCE的中位线,
∴CE=2AD=6;
(2)证明:∵CE∥AD,
∴∠BAD=∠E,∠CAD=∠ACE,
而∠BAD=∠CAD,
∴∠ACE=∠E,
∴AE=AC,
而AB=AE,
∴AB=AC,
∴△ABC为等腰三角形.
(3)如图,连接BP、BQ、CQ,
在Rt△ABD中,AB==5,
设⊙P的半径为R,⊙Q的半径为r,
在Rt△PBD中,(R﹣3)2+42=R2,解得R=,
∴PD=PA﹣AD=﹣3=,
∵S△ABQ+S△BCQ+S△ACQ=S△ABC,
∴?r?5+?r?8+?r?5=?3?8,解得r=,
即QD=,
∴PQ=PD+QD=+=.
答:△ABC的外接圆圆心P与内切圆圆心Q之间的距离为.
【点评】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等腰三角形的判定与性质和三角形的外接圆.
同课章节目录
