第23章解直角三角形全章教案
图片预览




文档简介
第23章 解直角三角形
23.1 锐角的三角函数
第1课时 正切与坡度
◇教学目标◇
【知识与技能】
能运用tan A表示直角三角形中的两边之比,表示物体的倾斜度、坡度等,能利用直角三角形中的边角关系进行简单的计算.
【过程与方法】
经历观察、猜想等数学活动过程,发展合情推理能力.
【情感、态度与价值观】
使学生在学习数学的过程中体会数学与生活的密切联系,激发学生学习数学的兴趣,增强学好数学的信心.
◇教学重难点◇
【教学重点】
对正切的理解,能运用正切函数表示直角三角形中两边的比.
【教学难点】
对坡度的理解并能运用来解决实际问题.
◇教学过程◇
一、情境导入
下列图中的两个台阶哪个更陡?你是怎么判断的?
二、合作探究
探究点1 正切的意义
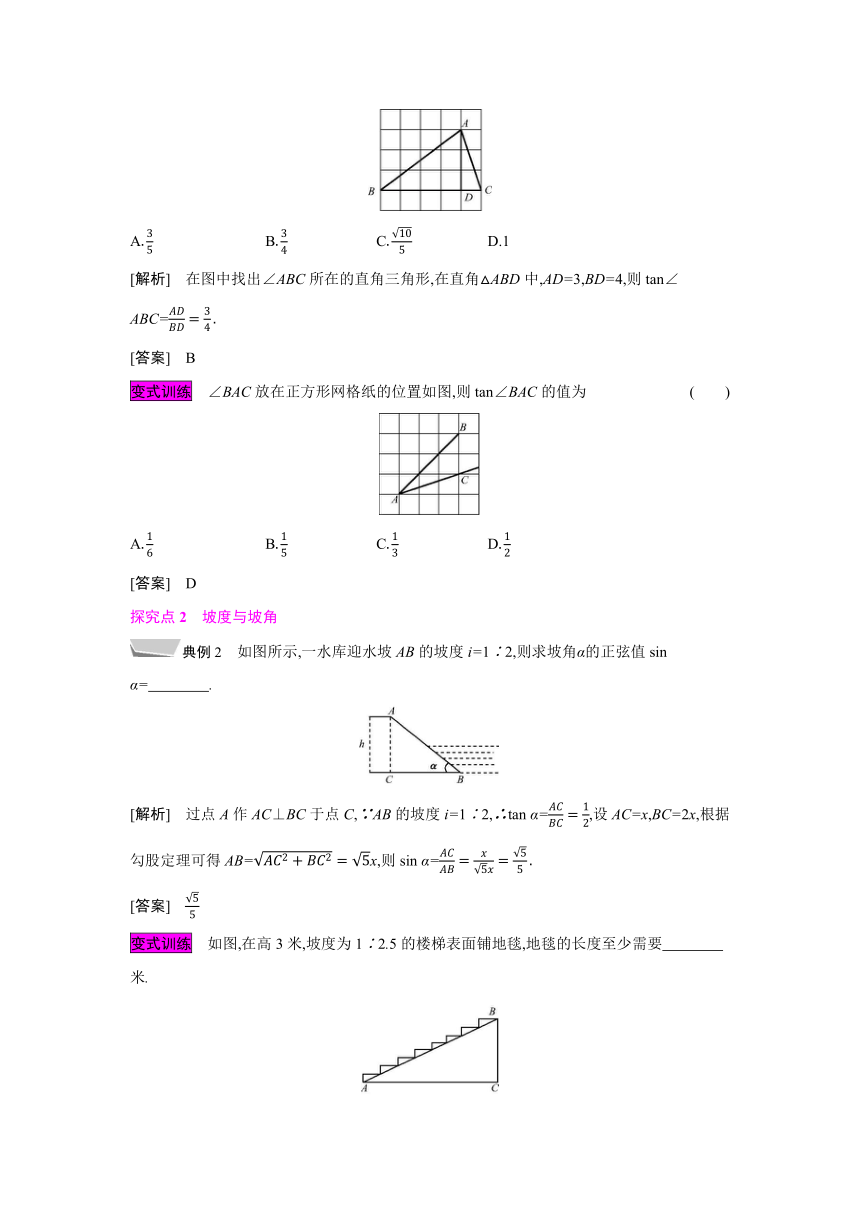
典例1 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为 ( )
A B C D.1
[解析] 在图中找出∠ABC所在的直角三角形,在直角△ABD中,AD=3,BD=4,则tan∠ABC=
[答案] B
变式训练 ∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为 ( )
A B C D
[答案] D
探究点2 坡度与坡角
典例2 如图所示,一水库迎水坡AB的坡度i=1∶2,则求坡角α的正弦值sin α= .?
[解析] 过点A作AC⊥BC于点C,∵AB的坡度i=1∶2,∴tan α=,设AC=x,BC=2x,根据勾股定理可得AB=x,则sin α=
[答案]
变式训练 如图,在高3米,坡度为1∶2.5的楼梯表面铺地毯,地毯的长度至少需要 米.?
[答案] 10.5
三、板书设计
正切与坡度
1.正切的概念:
在直角三角形ABC中,tan A=
2.坡度的概念:
坡度是坡面的铅直高度与水平宽度的比,也是坡角的正切值.
◇教学反思◇
三角函数不同于已学过的一次函数、反比例函数、二次函数,它的概念、形式和应用方式都不同,因此在最初学习如何应用时较为“别扭”,学生还处于模仿阶段,既要重视对题目的理解、形成一定的解题思路,也要重视书写格式.第2课时 正弦和余弦
◇教学目标◇
【知识与技能】
了解锐角三角函数的概念,能够正确应用sin A,cos A,tan A表示直角三角形中两边的比.
【过程与方法】
通过锐角三角函数的学习进一步认识函数,体会函数的变化与对应的思想,体会数学在解决实际问题中的应用.
【情感、态度与价值观】
培养学生的合作意识,提高学生学习数学的兴趣.
◇教学重难点◇
【教学重点】
锐角三角函数概念的理解.
【教学难点】
锐角三角函数的应用.
◇教学过程◇
一、情境导入
操场上有一个旗杆,老师让小明去测量旗杆高度.如图,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为
34°,并已知身高为1米,然后他很快就算出旗杆的高度了.你知道小明是怎样算出的吗?
二、合作探究
探究点1 正弦、余弦的概念
典例1 如图,在Rt△ABC中,∠C=90°,求sin A和sin B的值.
[解析] 如图(1),在Rt△ABC中,由勾股定理得AB==5.
因此sin A=,sin B=
如图(2),在Rt△ABC中,由勾股定理得AC==12.因此sin A=,sin B=
变式训练 在△ABC中,若AC∶BC∶AB=5∶12∶13,则sin A= ( )
A B C D
[答案] A
探究2 锐角三角函数
典例2 Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,根据下列条件计算∠A的三个三角函数值.
(1)a=2,b=;
(2)b∶c=2∶3.
[解析] (1)c==5,所以sin A=,cos A=,tan A=
(2)设b=2k,c=3k,a=k,
所以sin A=,cos A=,tan A=
变式训练
如图,在Rt△ABC中,∠C=90°,BC=6,sin A=,求cos A,tan B的值.
[解析] ∵sin A=,∴AB==6=10.
又∵AC==8,
∴cos A=,tan B=
三、板书设计
正弦和余弦
正弦和余弦
◇教学反思◇
本节课采用问题引入法,从探究性问题入手,让学生主动参与学习活动,用特殊值探究锐角的三角函数时,从作图、找边角、计算各个方面进行探究.
第3课时 30°,45°,60°角的三角函数值
◇教学目标◇
【知识与技能】
熟记30°,45°,60°角的三角函数值,并能根据这些值说出对应的锐角度数.
【过程与方法】
经历观察、操作、归纳等学习数学的过程,感受数学思考过程的合理性,感受数学说理的必要性、说理过程的严谨性,养成科学、严谨的学习态度.
【情感、态度与价值观】
培养学生把实际问题转化为数学问题的能力.
◇教学重难点◇
【教学重点】
30°,45°,60°角的三角函数值.
【教学难点】
与特殊角的三角函数值有关的计算.
◇教学过程◇
一、情境导入
观察一副三角板:它们其中有几个锐角?分别是多少度?它们的正弦、余弦、正切值又是多少呢?
二、合作探究
探究点1 30°,45°,60°特殊角的三角函数值
典例1 计算tan 60°+2sin 45°-2cos 30°的结果是 ( )
A.2 B C D.1
[解析] tan 60°+2sin 45°-2cos 30°=+2-2
[答案] C
变式训练 计算:(1)3tan 30°-tan 45°+2cos 30°+4sin 60°;
(2)|sin 45°-1|-+cos 45°-tan 60°.
[解析] (1)原式=-1++2=4-1.
(2)原式=1--1+=-
与特殊角三角函数值有关的运算,先写出每个角的函数值,然后转成实数运算,应注意此时运算的顺序和计算的方法.本题是一道与锐角三角函数值有关的计算问题,解决问题的关键是先确定函数值,然后再进行实数的运算.
探究点2 互余两角的正余弦之间的关系
典例2 若cos A=0.3521,则sin (90°-A)= .?
[解析] 根据互为余角的三角函数表达式,可得sin(90°-A)=cos A,又∵cos A=0.3521,∴sin (90°-A)=0.3521.
[答案] 0.3521
变式训练 (1)已知α为锐角,且sin α=cos 50°,则α= .?
(2)若sin 20°=cos (α+25°),则tan α= .?
[答案] (1)40°;(2)1.
三、板书设计
30°,45°,60°角的三角函数值
函数值角函数 sin α cos α tan α
30°
45° 1
60°
◇教学反思◇
三角尺是学生非常熟悉的学习用具,在这节课的教学中,教师应大胆地鼓励学生用所学的数学知识如“直角三角形中,30°角所对的边等于斜边的一半”的特性,经历探索30°,45°,60°角的三角函数值的过程,发展学生的推理能力和计算能力.给学生留充分的时间,采取多种形式让学生记住特殊角的三角函数值.
第4课时 一般锐角的三角函数值
◇教学目标◇
【知识与技能】
1.会使用计算器求锐角的三角函数值;
2.会使用计算器根据锐角三角函数的值求对应的锐角.
【过程与方法】
在做题、计算的过程中,逐步熟悉计算器的使用方法.
【情感、态度与价值观】
经历计算器的使用过程,可激发学生的学习兴趣.
◇教学重难点◇
【教学重点】
利用计算器求锐角三角函数的值.
【教学难点】
计算器的按键顺序.
◇教学过程◇
一、情境导入
通过上面几节的学习我们知道,当锐角A是30°,45°或60°等特殊角时,可以求得这些特殊角的正弦值、余弦值和正切值;如果锐角A不是这些特殊角,怎样得到它的三角函数值呢?
二、合作探究
探究点1 用计算器一般锐角三角函数值
典例1 用计算器计算(1)sin 56°;(2)sin 15°49';(3)cos 20°;(4)tan 29°;(5)tan 44°59'59″;(6)sin 15°+cos 61°+tan 76°.
[解析] (1)sin 56°≈0.8290.
(2)sin 15°49'≈0.2726.
(3)cos 20°≈0.9397.
(4)tan 29°≈0.5543.
(5)tan 44°59'59″≈1.0000.
(6)sin 15°+cos 61°+tan 76°≈0.2588+0.4848+4.0108=4.7544.
探究点2 由锐角三角函数值求角度
典例2 求满足下列条件的∠A的度数(精确到1″):
(1)cos A=0.8607;
(2)tan A=56.78.
[解析] (1)∵cos A=0.8607,
∴∠A≈30.605°=30°36'18″.
(2)∵tan A=56.78,
∴∠A≈88.991°≈88°59'28″.
探究点3 三角函数的应用
典例3
如图所示,通过计算可以求得某市在冬至日正午时分的太阳光线入射角为30°30',因此在规划建设楼高为20 m的小区时,两楼间的距离至少为 米才能保证不挡光.(精确到0.01)?
[解析] 如图所示,太阳的光线和水平地面、楼高形成Rt△ABC,当两楼间的距离为线段AC时,才能保证不挡光.
在Rt△ABC中,∠A=30°30',BC=20 m.
∵tan∠BAC=,∴AC=33.96(m).
故当两楼间的距离至少为33.96 m时,才能保证不挡光.
[答案] 33.96
三、板书设计
一般锐角的三角函数值
1.利用计算器求锐角的三角函数值,已知锐角三角函数值用计算器求出相应的锐角.
2.锐角三角函数值的增减性:对于sin A与tan A,角度越大函数值也越大;对于cos A,角度越大函数值越小.
◇教学反思◇
本节是学习用计算器求三角函数值并加以实际应用的内容,通过本节的学习,可以使学生充分认识到三角函数知识在现实世界中有着广泛的应用.
23.2 解直角三角形及其应用
第1课时 解直角三角形
◇教学目标◇
【知识与技能】
在理解解直角三角形的含义、直角三角形五个元素之间关系的基础上,会运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.
【过程与方法】
经历运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形的过程,逐步培养学生分析问题、解决问题的能力.
【情感、态度与价值观】
在探究学习的过程中,让学生在学习过程中感受到成功的喜悦,产生后继学习的激情,增强学好数学的信心.
◇教学重难点◇
【教学重点】
直角三角形的解法.
【教学难点】
灵活运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.
◇教学过程◇
一、情境导入
据报道:始建于1350年的意大利比萨斜塔落成时就已经倾斜.1972年比萨发生地震,这座高54.5 m的斜塔大幅度摇摆22分之多,仍巍然屹立.可是,塔顶中心点偏离垂直中心线的距离已由落成时的2.1 m增加至5.2 m,而且还以每年倾斜1 cm的速度继续增加,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔进行维修纠偏,2001年竣工,使塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8 cm.
根据上面的这段报道中,“塔顶中心点偏离垂直中心线的距离已由落成时的2.1 m增加至5.2 m”这句话你是怎样理解的,它能用来描述比萨斜塔的倾斜程度吗?
二、合作探究
探究点 解直角三角形
典例 在Rt△ABC中,∠C=90°,a,b,c是△ABC的三边,a=6,∠B=30°,求∠A,b,c.
[解析] ∵∠A+∠B=90°,∴∠A=90°-∠B=60°.
∵tan B=,
∴b=a·tan B=6×tan 30°=6=2
又∵cos B=,∴c==4,
∴∠A=60°,b=2,c=4
直角三角形中有关边角解法的几种类型
(1)已知一个锐角∠A和一条直角边a时,则∠B=90°-∠A,c=,b=(或b=).
(2)已知两直角边a,b,则c=,由tan A=,可求∠A,则∠B=90°-∠A.
(3)已知一斜边和一锐角,如c,∠A,则∠B=90°-∠A,a=c·sin A,b=c·cos A(或b=).
变式训练 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知a=3,b=3,求c,∠A,∠B.
(2)已知b=5,c=10,求a,∠A,∠B.
(3)已知∠A=45°,c=8,求a,b,∠B.
[解析] (1)根据勾股定理得c==3
又∵tan A==1,∴∠A=45°.
又∵∠A+∠B=90,∴∠B=45°.
(2)根据勾股定理得a==5,
又∵sin B=,∴∠B=30°.
又∵∠A+∠B=90°,∴∠A=60°.
(3)∵sin A=,∴a=c·sin A=8×sin 45°=4,
又∵cos A=,∴b=c·cos A=8×cos 45°=4,
又∵∠A+∠B=90°,∴∠B=45°.
【归纳提升】解直角三角形时需要注意的几个问题:
①尽量使用原始数据,少用有误差的近似值,使计算更加准确;②非直角三角形问题,通过添加恰当的辅助线转化为解直角三角形问题;③恰当使用方程可使一些较复杂的解直角三角形问题化繁为简、化难为易;④在选用三角函数时,尽可能做乘法,避免除法,以使运算简便.
三、板书设计
解直角三角形
解直角
三角形
的方法
◇教学反思◇
本节课在教学过程中,能灵活处理教材,敢于放手让学生通过自主学习、合作探究达到理解并掌握知识的目的,并能运用知识解决问题.
第2课时 仰角俯角中的三角函数
◇教学目标◇
【知识与技能】
使学生掌握仰角、俯角的概念,并会正确运用这些概念和解直角三角形的知识解决一些实际问题.
【过程与方法】
让学生体验方程思想和数形结合思想在解直角三角形中的用途.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
将实际问题转化为解直角三角形问题.
【教学难点】
将实际问题中的数量关系转化为直角三角形中元素间的关系求解.
◇教学过程◇
一、情境导入
某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹竿的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度,若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度.
二、合作探究
探究点 仰角、俯角问题
典例 在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin 20°,cos 20°,tan 20°)
[解析] 由题意得∠ABC=90°,
∵∠ACB=45°,∴∠CAB=90°-∠ACB=90°-45°=45°,∴AB=BC.
设AB=x,则BC=x,DB=20+x,
在Rt△ABD中,∵tan∠ADB=,
∴tan 20°=
∵tan 20°,,x=11.25.
∵BM=CE=1.5,
∴AM=11.25+1.5=12.75.
答:教学楼的高AM是12.75米.
变式训练
如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼BC的高度.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
[解析] 过点E,D分别作BC的垂线,交BC于点F,G.
在Rt△EFC中,因为FC=AE=20,∠FEC=45°,
所以EF=20,在Rt△DBG中,DG=EF=20,∠BDG=37°,
因为tan∠BDG=0.75,
所以BG≈DG×0.75=20×0.75=15,
又GF=DE=5,
所以BC=BG+GF+FC=15+5+20=40.
答:大楼BC的高度是40米.
三、板书设计
俯角仰角中的三角函数
仰角与俯角
◇教学反思◇
本节课的主要内容是掌握仰角、俯角等概念,使学生能初步用解直角三角形的相关知识解决一些实际问题.
第3课时 方位角
◇教学目标◇
【知识与技能】
会运用解直角三角形的知识解决与方位角问题有关的实际问题.
【过程与方法】
逐步培养学生分析问题、解决问题的能力,渗透数形结合的思想方法.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
解决方位角问题的实际问题.
【教学难点】
理解方位角的概念和有关术语.
◇教学过程◇
一、情境导入
在我们的某一方向有一物体,应怎样确定其方向呢?
二、合作探究
探究点 方位角的应用
典例1 据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据:1.4,1.7)
[解析] 在Rt△BCD中,
∵∠BDC=90°,∠BCD=45°,CD=100米,
∴BD=CD=100米.
在Rt△ACD中,∵∠ADC=90°,∠ACD=60°,CD=100米,
∴AD=CD·tan∠ACD=100(米).
∴AB=AD-BD=100-100≈70(米).
∴此车的速度为=17.5(米/秒).
∵17.5>16,
∴此车超过了该路段16米/秒的限制速度.
典例2 钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.
[解析] 在直角△ACM,∠CAM=45°,则△ACM是等腰直角三角形,
则AC=CM=12,∴BC=AC-AB=12-4=8,
直角△BCN中,CN=BC·tan∠CBN=BC=8,∴MN=CN-CM=8-12(海里).
答:钓鱼岛东西两端点MN之间的距离是(8-12)海里.
三、板书设计
方位角
1.方位角的定义
2.方位角的应用
◇教学反思◇
这节课,对学生来说有一定的难度,解直角三角形的应用对学生来说是一个难点.教学中应体现“问题情境——建立数学模型——应用与拓展”的模式,选择有现实意义的内容,目的是让学生掌握方位角的知识,进一步提高学生观察、分析、概括和抽象等能力.
第4课时 倾斜程度与三角函数
◇教学目标◇
【知识与技能】
会运用解直角三角形的知识解决与坡度、坡角等有关的实际问题.
【过程与方法】
逐步培养学生分析问题、解决问题的能力,渗透数形结合的思想方法.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
解决有关坡度的实际问题.
【教学难点】
理解坡度的概念和有关术语.
◇教学过程◇
一、情境导入
在现实生活中,经常会有建筑大坝、修地基等,它们的截面上底和下底不是同样宽的,侧面是有斜坡的,且倾斜程度是不一样的,这些在设计图纸上都要注明,以便施工时遵循.
二、合作探究
探究点1 与坡度坡角有关问题
典例1 如图,某地下车库的入口处有斜坡AB,它的坡度为i=1∶2,斜坡AB的长为6米,车库的高度为AH(AH⊥BC),为了让行车更安全,现将斜坡的坡角改造为14°(图中的∠ACB=14°).
(1)求车库的高度AH;
(2)求点B与点C之间的距离(结果精确到1米).
(参考数据:sin 14°=0.24,cos 14°=0.97,tan 14°=0.25)
[解析] (1)由题意可得AH∶BH=1∶2,
设AH=x,则BH=2x,故x2+(2x)2=(6)2,
解得x=6,
答:车库的高度AH为6 m.
(2)∵AH=6,∴BH=2AH=12,
∴CH=BC+BH=BC+12,
在Rt△AHC中,∠AHC=90°,故tan∠ACB=,
又∵∠ACB=14°,∴tan 14°=,∴0.25=,解得BC=12.
答:点B与点C之间的距离是12 m.
与坡角、坡度相关的实际问题解题思路
(1)弄清直角三角形的有关知识解实际中的有关仰坡角、水平距离、垂直距离、水平等概念的意义.
(2)要认真分析题意,画出示意图并找出需要求解的直角三角形.
(3)将实际问题中的数量关系归纳为直角三角形中元素间的关系,再解这个三角形.
探究点2 直线的斜率与倾斜角之间关系
典例2 求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)P1(1,3),P2(4,6);
(2)Q1(-1,6),Q2(-1,3).
[解析] (1)∵P1(1,3),P2(4,6),
=1,
则其倾斜角是45°,为锐角.
(2)∵Q1(-1,6),Q2(-1,3),
∴直线Q1Q2的斜率不存在,其倾斜角为90°,是直角.
变式训练 经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点.求直线l斜率k的范围.
[解析] kPA==-1,
kPB==1,
∵l与线段AB相交,
∴kpA≤k≤kpB,
∴-1≤k≤1.
三、板书设计
倾斜程度与三角函数
倾斜程度与
三角函数
◇教学反思◇
在教学过程中要多给学生提供练习的机会,让学生自己来作辅助线.在解直角三角形时让学生讨论,各抒己见.在有多种方法时,让学生讨论哪一种方法简单.
23.1 锐角的三角函数
第1课时 正切与坡度
◇教学目标◇
【知识与技能】
能运用tan A表示直角三角形中的两边之比,表示物体的倾斜度、坡度等,能利用直角三角形中的边角关系进行简单的计算.
【过程与方法】
经历观察、猜想等数学活动过程,发展合情推理能力.
【情感、态度与价值观】
使学生在学习数学的过程中体会数学与生活的密切联系,激发学生学习数学的兴趣,增强学好数学的信心.
◇教学重难点◇
【教学重点】
对正切的理解,能运用正切函数表示直角三角形中两边的比.
【教学难点】
对坡度的理解并能运用来解决实际问题.
◇教学过程◇
一、情境导入
下列图中的两个台阶哪个更陡?你是怎么判断的?
二、合作探究
探究点1 正切的意义
典例1 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为 ( )
A B C D.1
[解析] 在图中找出∠ABC所在的直角三角形,在直角△ABD中,AD=3,BD=4,则tan∠ABC=
[答案] B
变式训练 ∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为 ( )
A B C D
[答案] D
探究点2 坡度与坡角
典例2 如图所示,一水库迎水坡AB的坡度i=1∶2,则求坡角α的正弦值sin α= .?
[解析] 过点A作AC⊥BC于点C,∵AB的坡度i=1∶2,∴tan α=,设AC=x,BC=2x,根据勾股定理可得AB=x,则sin α=
[答案]
变式训练 如图,在高3米,坡度为1∶2.5的楼梯表面铺地毯,地毯的长度至少需要 米.?
[答案] 10.5
三、板书设计
正切与坡度
1.正切的概念:
在直角三角形ABC中,tan A=
2.坡度的概念:
坡度是坡面的铅直高度与水平宽度的比,也是坡角的正切值.
◇教学反思◇
三角函数不同于已学过的一次函数、反比例函数、二次函数,它的概念、形式和应用方式都不同,因此在最初学习如何应用时较为“别扭”,学生还处于模仿阶段,既要重视对题目的理解、形成一定的解题思路,也要重视书写格式.第2课时 正弦和余弦
◇教学目标◇
【知识与技能】
了解锐角三角函数的概念,能够正确应用sin A,cos A,tan A表示直角三角形中两边的比.
【过程与方法】
通过锐角三角函数的学习进一步认识函数,体会函数的变化与对应的思想,体会数学在解决实际问题中的应用.
【情感、态度与价值观】
培养学生的合作意识,提高学生学习数学的兴趣.
◇教学重难点◇
【教学重点】
锐角三角函数概念的理解.
【教学难点】
锐角三角函数的应用.
◇教学过程◇
一、情境导入
操场上有一个旗杆,老师让小明去测量旗杆高度.如图,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为
34°,并已知身高为1米,然后他很快就算出旗杆的高度了.你知道小明是怎样算出的吗?
二、合作探究
探究点1 正弦、余弦的概念
典例1 如图,在Rt△ABC中,∠C=90°,求sin A和sin B的值.
[解析] 如图(1),在Rt△ABC中,由勾股定理得AB==5.
因此sin A=,sin B=
如图(2),在Rt△ABC中,由勾股定理得AC==12.因此sin A=,sin B=
变式训练 在△ABC中,若AC∶BC∶AB=5∶12∶13,则sin A= ( )
A B C D
[答案] A
探究2 锐角三角函数
典例2 Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,根据下列条件计算∠A的三个三角函数值.
(1)a=2,b=;
(2)b∶c=2∶3.
[解析] (1)c==5,所以sin A=,cos A=,tan A=
(2)设b=2k,c=3k,a=k,
所以sin A=,cos A=,tan A=
变式训练
如图,在Rt△ABC中,∠C=90°,BC=6,sin A=,求cos A,tan B的值.
[解析] ∵sin A=,∴AB==6=10.
又∵AC==8,
∴cos A=,tan B=
三、板书设计
正弦和余弦
正弦和余弦
◇教学反思◇
本节课采用问题引入法,从探究性问题入手,让学生主动参与学习活动,用特殊值探究锐角的三角函数时,从作图、找边角、计算各个方面进行探究.
第3课时 30°,45°,60°角的三角函数值
◇教学目标◇
【知识与技能】
熟记30°,45°,60°角的三角函数值,并能根据这些值说出对应的锐角度数.
【过程与方法】
经历观察、操作、归纳等学习数学的过程,感受数学思考过程的合理性,感受数学说理的必要性、说理过程的严谨性,养成科学、严谨的学习态度.
【情感、态度与价值观】
培养学生把实际问题转化为数学问题的能力.
◇教学重难点◇
【教学重点】
30°,45°,60°角的三角函数值.
【教学难点】
与特殊角的三角函数值有关的计算.
◇教学过程◇
一、情境导入
观察一副三角板:它们其中有几个锐角?分别是多少度?它们的正弦、余弦、正切值又是多少呢?
二、合作探究
探究点1 30°,45°,60°特殊角的三角函数值
典例1 计算tan 60°+2sin 45°-2cos 30°的结果是 ( )
A.2 B C D.1
[解析] tan 60°+2sin 45°-2cos 30°=+2-2
[答案] C
变式训练 计算:(1)3tan 30°-tan 45°+2cos 30°+4sin 60°;
(2)|sin 45°-1|-+cos 45°-tan 60°.
[解析] (1)原式=-1++2=4-1.
(2)原式=1--1+=-
与特殊角三角函数值有关的运算,先写出每个角的函数值,然后转成实数运算,应注意此时运算的顺序和计算的方法.本题是一道与锐角三角函数值有关的计算问题,解决问题的关键是先确定函数值,然后再进行实数的运算.
探究点2 互余两角的正余弦之间的关系
典例2 若cos A=0.3521,则sin (90°-A)= .?
[解析] 根据互为余角的三角函数表达式,可得sin(90°-A)=cos A,又∵cos A=0.3521,∴sin (90°-A)=0.3521.
[答案] 0.3521
变式训练 (1)已知α为锐角,且sin α=cos 50°,则α= .?
(2)若sin 20°=cos (α+25°),则tan α= .?
[答案] (1)40°;(2)1.
三、板书设计
30°,45°,60°角的三角函数值
函数值角函数 sin α cos α tan α
30°
45° 1
60°
◇教学反思◇
三角尺是学生非常熟悉的学习用具,在这节课的教学中,教师应大胆地鼓励学生用所学的数学知识如“直角三角形中,30°角所对的边等于斜边的一半”的特性,经历探索30°,45°,60°角的三角函数值的过程,发展学生的推理能力和计算能力.给学生留充分的时间,采取多种形式让学生记住特殊角的三角函数值.
第4课时 一般锐角的三角函数值
◇教学目标◇
【知识与技能】
1.会使用计算器求锐角的三角函数值;
2.会使用计算器根据锐角三角函数的值求对应的锐角.
【过程与方法】
在做题、计算的过程中,逐步熟悉计算器的使用方法.
【情感、态度与价值观】
经历计算器的使用过程,可激发学生的学习兴趣.
◇教学重难点◇
【教学重点】
利用计算器求锐角三角函数的值.
【教学难点】
计算器的按键顺序.
◇教学过程◇
一、情境导入
通过上面几节的学习我们知道,当锐角A是30°,45°或60°等特殊角时,可以求得这些特殊角的正弦值、余弦值和正切值;如果锐角A不是这些特殊角,怎样得到它的三角函数值呢?
二、合作探究
探究点1 用计算器一般锐角三角函数值
典例1 用计算器计算(1)sin 56°;(2)sin 15°49';(3)cos 20°;(4)tan 29°;(5)tan 44°59'59″;(6)sin 15°+cos 61°+tan 76°.
[解析] (1)sin 56°≈0.8290.
(2)sin 15°49'≈0.2726.
(3)cos 20°≈0.9397.
(4)tan 29°≈0.5543.
(5)tan 44°59'59″≈1.0000.
(6)sin 15°+cos 61°+tan 76°≈0.2588+0.4848+4.0108=4.7544.
探究点2 由锐角三角函数值求角度
典例2 求满足下列条件的∠A的度数(精确到1″):
(1)cos A=0.8607;
(2)tan A=56.78.
[解析] (1)∵cos A=0.8607,
∴∠A≈30.605°=30°36'18″.
(2)∵tan A=56.78,
∴∠A≈88.991°≈88°59'28″.
探究点3 三角函数的应用
典例3
如图所示,通过计算可以求得某市在冬至日正午时分的太阳光线入射角为30°30',因此在规划建设楼高为20 m的小区时,两楼间的距离至少为 米才能保证不挡光.(精确到0.01)?
[解析] 如图所示,太阳的光线和水平地面、楼高形成Rt△ABC,当两楼间的距离为线段AC时,才能保证不挡光.
在Rt△ABC中,∠A=30°30',BC=20 m.
∵tan∠BAC=,∴AC=33.96(m).
故当两楼间的距离至少为33.96 m时,才能保证不挡光.
[答案] 33.96
三、板书设计
一般锐角的三角函数值
1.利用计算器求锐角的三角函数值,已知锐角三角函数值用计算器求出相应的锐角.
2.锐角三角函数值的增减性:对于sin A与tan A,角度越大函数值也越大;对于cos A,角度越大函数值越小.
◇教学反思◇
本节是学习用计算器求三角函数值并加以实际应用的内容,通过本节的学习,可以使学生充分认识到三角函数知识在现实世界中有着广泛的应用.
23.2 解直角三角形及其应用
第1课时 解直角三角形
◇教学目标◇
【知识与技能】
在理解解直角三角形的含义、直角三角形五个元素之间关系的基础上,会运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.
【过程与方法】
经历运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形的过程,逐步培养学生分析问题、解决问题的能力.
【情感、态度与价值观】
在探究学习的过程中,让学生在学习过程中感受到成功的喜悦,产生后继学习的激情,增强学好数学的信心.
◇教学重难点◇
【教学重点】
直角三角形的解法.
【教学难点】
灵活运用勾股定理、直角三角形的两锐角互余及锐角三角函数解直角三角形.
◇教学过程◇
一、情境导入
据报道:始建于1350年的意大利比萨斜塔落成时就已经倾斜.1972年比萨发生地震,这座高54.5 m的斜塔大幅度摇摆22分之多,仍巍然屹立.可是,塔顶中心点偏离垂直中心线的距离已由落成时的2.1 m增加至5.2 m,而且还以每年倾斜1 cm的速度继续增加,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔进行维修纠偏,2001年竣工,使塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8 cm.
根据上面的这段报道中,“塔顶中心点偏离垂直中心线的距离已由落成时的2.1 m增加至5.2 m”这句话你是怎样理解的,它能用来描述比萨斜塔的倾斜程度吗?
二、合作探究
探究点 解直角三角形
典例 在Rt△ABC中,∠C=90°,a,b,c是△ABC的三边,a=6,∠B=30°,求∠A,b,c.
[解析] ∵∠A+∠B=90°,∴∠A=90°-∠B=60°.
∵tan B=,
∴b=a·tan B=6×tan 30°=6=2
又∵cos B=,∴c==4,
∴∠A=60°,b=2,c=4
直角三角形中有关边角解法的几种类型
(1)已知一个锐角∠A和一条直角边a时,则∠B=90°-∠A,c=,b=(或b=).
(2)已知两直角边a,b,则c=,由tan A=,可求∠A,则∠B=90°-∠A.
(3)已知一斜边和一锐角,如c,∠A,则∠B=90°-∠A,a=c·sin A,b=c·cos A(或b=).
变式训练 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知a=3,b=3,求c,∠A,∠B.
(2)已知b=5,c=10,求a,∠A,∠B.
(3)已知∠A=45°,c=8,求a,b,∠B.
[解析] (1)根据勾股定理得c==3
又∵tan A==1,∴∠A=45°.
又∵∠A+∠B=90,∴∠B=45°.
(2)根据勾股定理得a==5,
又∵sin B=,∴∠B=30°.
又∵∠A+∠B=90°,∴∠A=60°.
(3)∵sin A=,∴a=c·sin A=8×sin 45°=4,
又∵cos A=,∴b=c·cos A=8×cos 45°=4,
又∵∠A+∠B=90°,∴∠B=45°.
【归纳提升】解直角三角形时需要注意的几个问题:
①尽量使用原始数据,少用有误差的近似值,使计算更加准确;②非直角三角形问题,通过添加恰当的辅助线转化为解直角三角形问题;③恰当使用方程可使一些较复杂的解直角三角形问题化繁为简、化难为易;④在选用三角函数时,尽可能做乘法,避免除法,以使运算简便.
三、板书设计
解直角三角形
解直角
三角形
的方法
◇教学反思◇
本节课在教学过程中,能灵活处理教材,敢于放手让学生通过自主学习、合作探究达到理解并掌握知识的目的,并能运用知识解决问题.
第2课时 仰角俯角中的三角函数
◇教学目标◇
【知识与技能】
使学生掌握仰角、俯角的概念,并会正确运用这些概念和解直角三角形的知识解决一些实际问题.
【过程与方法】
让学生体验方程思想和数形结合思想在解直角三角形中的用途.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
将实际问题转化为解直角三角形问题.
【教学难点】
将实际问题中的数量关系转化为直角三角形中元素间的关系求解.
◇教学过程◇
一、情境导入
某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹竿的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度,若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度.
二、合作探究
探究点 仰角、俯角问题
典例 在数学课外实践活动中,要测量教学楼的高度AM.下面是两位同学的对话:
请你根据两位同学的对话,结合图形计算教学楼的高度AM.(参考数据:sin 20°,cos 20°,tan 20°)
[解析] 由题意得∠ABC=90°,
∵∠ACB=45°,∴∠CAB=90°-∠ACB=90°-45°=45°,∴AB=BC.
设AB=x,则BC=x,DB=20+x,
在Rt△ABD中,∵tan∠ADB=,
∴tan 20°=
∵tan 20°,,x=11.25.
∵BM=CE=1.5,
∴AM=11.25+1.5=12.75.
答:教学楼的高AM是12.75米.
变式训练
如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼BC的高度.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
[解析] 过点E,D分别作BC的垂线,交BC于点F,G.
在Rt△EFC中,因为FC=AE=20,∠FEC=45°,
所以EF=20,在Rt△DBG中,DG=EF=20,∠BDG=37°,
因为tan∠BDG=0.75,
所以BG≈DG×0.75=20×0.75=15,
又GF=DE=5,
所以BC=BG+GF+FC=15+5+20=40.
答:大楼BC的高度是40米.
三、板书设计
俯角仰角中的三角函数
仰角与俯角
◇教学反思◇
本节课的主要内容是掌握仰角、俯角等概念,使学生能初步用解直角三角形的相关知识解决一些实际问题.
第3课时 方位角
◇教学目标◇
【知识与技能】
会运用解直角三角形的知识解决与方位角问题有关的实际问题.
【过程与方法】
逐步培养学生分析问题、解决问题的能力,渗透数形结合的思想方法.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
解决方位角问题的实际问题.
【教学难点】
理解方位角的概念和有关术语.
◇教学过程◇
一、情境导入
在我们的某一方向有一物体,应怎样确定其方向呢?
二、合作探究
探究点 方位角的应用
典例1 据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据:1.4,1.7)
[解析] 在Rt△BCD中,
∵∠BDC=90°,∠BCD=45°,CD=100米,
∴BD=CD=100米.
在Rt△ACD中,∵∠ADC=90°,∠ACD=60°,CD=100米,
∴AD=CD·tan∠ACD=100(米).
∴AB=AD-BD=100-100≈70(米).
∴此车的速度为=17.5(米/秒).
∵17.5>16,
∴此车超过了该路段16米/秒的限制速度.
典例2 钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.
[解析] 在直角△ACM,∠CAM=45°,则△ACM是等腰直角三角形,
则AC=CM=12,∴BC=AC-AB=12-4=8,
直角△BCN中,CN=BC·tan∠CBN=BC=8,∴MN=CN-CM=8-12(海里).
答:钓鱼岛东西两端点MN之间的距离是(8-12)海里.
三、板书设计
方位角
1.方位角的定义
2.方位角的应用
◇教学反思◇
这节课,对学生来说有一定的难度,解直角三角形的应用对学生来说是一个难点.教学中应体现“问题情境——建立数学模型——应用与拓展”的模式,选择有现实意义的内容,目的是让学生掌握方位角的知识,进一步提高学生观察、分析、概括和抽象等能力.
第4课时 倾斜程度与三角函数
◇教学目标◇
【知识与技能】
会运用解直角三角形的知识解决与坡度、坡角等有关的实际问题.
【过程与方法】
逐步培养学生分析问题、解决问题的能力,渗透数形结合的思想方法.
【情感、态度与价值观】
使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
◇教学重难点◇
【教学重点】
解决有关坡度的实际问题.
【教学难点】
理解坡度的概念和有关术语.
◇教学过程◇
一、情境导入
在现实生活中,经常会有建筑大坝、修地基等,它们的截面上底和下底不是同样宽的,侧面是有斜坡的,且倾斜程度是不一样的,这些在设计图纸上都要注明,以便施工时遵循.
二、合作探究
探究点1 与坡度坡角有关问题
典例1 如图,某地下车库的入口处有斜坡AB,它的坡度为i=1∶2,斜坡AB的长为6米,车库的高度为AH(AH⊥BC),为了让行车更安全,现将斜坡的坡角改造为14°(图中的∠ACB=14°).
(1)求车库的高度AH;
(2)求点B与点C之间的距离(结果精确到1米).
(参考数据:sin 14°=0.24,cos 14°=0.97,tan 14°=0.25)
[解析] (1)由题意可得AH∶BH=1∶2,
设AH=x,则BH=2x,故x2+(2x)2=(6)2,
解得x=6,
答:车库的高度AH为6 m.
(2)∵AH=6,∴BH=2AH=12,
∴CH=BC+BH=BC+12,
在Rt△AHC中,∠AHC=90°,故tan∠ACB=,
又∵∠ACB=14°,∴tan 14°=,∴0.25=,解得BC=12.
答:点B与点C之间的距离是12 m.
与坡角、坡度相关的实际问题解题思路
(1)弄清直角三角形的有关知识解实际中的有关仰坡角、水平距离、垂直距离、水平等概念的意义.
(2)要认真分析题意,画出示意图并找出需要求解的直角三角形.
(3)将实际问题中的数量关系归纳为直角三角形中元素间的关系,再解这个三角形.
探究点2 直线的斜率与倾斜角之间关系
典例2 求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.
(1)P1(1,3),P2(4,6);
(2)Q1(-1,6),Q2(-1,3).
[解析] (1)∵P1(1,3),P2(4,6),
=1,
则其倾斜角是45°,为锐角.
(2)∵Q1(-1,6),Q2(-1,3),
∴直线Q1Q2的斜率不存在,其倾斜角为90°,是直角.
变式训练 经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点.求直线l斜率k的范围.
[解析] kPA==-1,
kPB==1,
∵l与线段AB相交,
∴kpA≤k≤kpB,
∴-1≤k≤1.
三、板书设计
倾斜程度与三角函数
倾斜程度与
三角函数
◇教学反思◇
在教学过程中要多给学生提供练习的机会,让学生自己来作辅助线.在解直角三角形时让学生讨论,各抒己见.在有多种方法时,让学生讨论哪一种方法简单.
