江西省南康中学2018-2019学年高一上学期第一次月考数学试题+Word版含答案
文档属性
| 名称 | 江西省南康中学2018-2019学年高一上学期第一次月考数学试题+Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-17 00:00:00 | ||
图片预览



文档简介
南康中学2018~2019学年度第一学期高一第一次大考
数 学 试 卷
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
1.把集合用列举法表示为( )
A.{,} B.{x|或}
C.{} D.{}
2.下列对应关系:
①,,的平方根;
②,的倒数;
③,;
④,,.
其中是到的映射的是( )
A. ①③ B.②④ C. ②③ D. ③④
3.已知,则( )
A.2 B.3 C.4 D.5
4. 已知集合,集合,则与的关系是( )
A. B. C. D. 且
5.已知集合 则( )
A.[2,3] B. C.[1,2) D.
6.下列函数中,在上为增函数的是( )
A. B. C. D.
7.如图的曲线是幂函数在第一象限内的图象,已知分别取,2四个值,相应曲线、、、的依次为( )
A. B.
C. D.
8.已知是定义在上是减函数,则的取值范围是( )
A. B. C. D.
9.已知函数,且,则下列不等式中成立的是( )
A. B.
C. D.
10.函数在单调递减,且为奇函数.若,则满足的的取值范围是( )
A. B. C. D.
11.若、是关于的方程()的两个实根,则 的最大值等于( )
A.6 B. C.18 D.19
12.若函数是偶函数,则的最小值为( )
A. B. C. D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分。将答案填在答题卡上的相应位置)
13.设集合,.若,则 .(用列举法表示)
14.已知集合,则 .
15.已知函数的值域为,则实数的取值范围为
16.给出定义:若 (其中为整数),则叫做离实数最近的整数,记作.在此基础上给出下列关于函数的四个结论:
①函数的定义域为,值域为;
②函数的图象关于直线对称;
③函数是偶函数;④函数在上是增函数.
其中正确的结论的序号是________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17. (本小题满分10分)
设函数的定义域为集合,已知集合,,全集为.
(I)求;
(II)若,求实数的取值范围.
18.(本小题满分12分)
已知集合,.
(Ⅰ) 当时,集合的元素中整数有多少个?
(Ⅱ)若,求实数的取值范围.
19.(本小题满分12分)
已知函数是定义在R上的偶函数,已知当时, .
(1)求函数的解析式;
(2)画出函数的图象,并写出函数的单调递增区间;
(3)试确定方程的解个数.
20.(本小题满分12分)
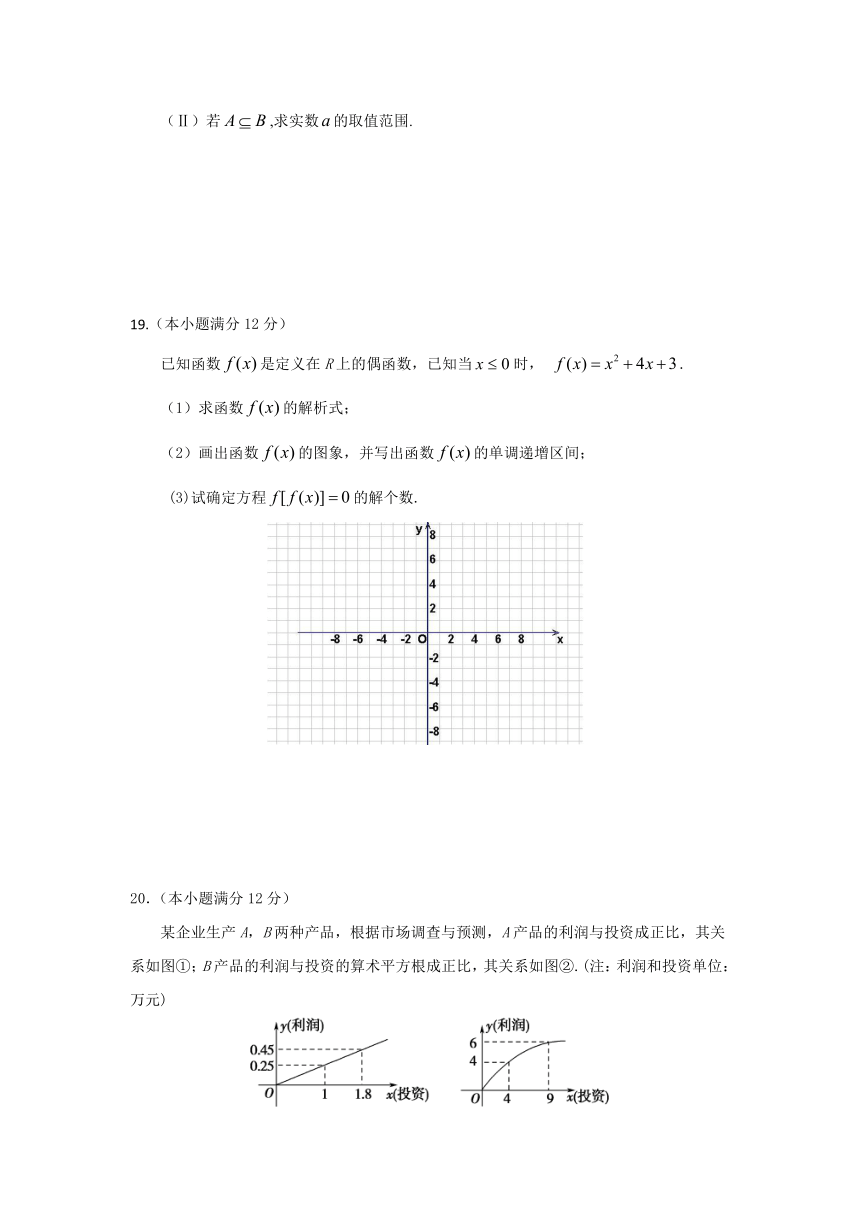
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
① ②
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
21. (本小题满分12分)
已知函数是定义在上的奇函数,且
(1)确定函数的解析式;
(2)判断函数在定义域内的单调性,并用定义证明;
(3解不等式.
22. (本小题满分12分)
已知幂函数在上单调递增.
(1)求实数的值,并写出函数的解析式;
(2)对于(1)中的函数,试判断是否存在整数,使函数在上的最大值为,若存在,求出的值;若不存在,请说明理由;
(3)设函数,若不等式对任意的恒成立,求实数的取值范围.
南康中学2018~2019学年度第一学期高一第一次大考
数学参考答案
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
A
C
B
B
B
A
C
D
C
C
二、填空题(本大题共4小题,每小题5分,共20分。将答案填在答题卡上的相应位置)
13. 14. 15. 16. ①②③
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
; ---------------5分
即实数的取值范围为. ---------------10分
注:第(1)问5分,第二问7分.
19.(1)当x>0时,-x<0 ∴f(-x)=(-x)2+4(-x)+3=x2-4x+3
∴f(x)为R上的偶函数 ∴f(-x)= f(x)= x2-4x+3
∴ --------------4分
(2)的图像略, --------------6分
f(x)单调增区间为和. ---------------8分
(3)有图知或,从而知方程有10个解. ---------------12分
20.(1)根据题意可设,。---------2分
则f(x)=0.25x(x≥0),g(x)=2 (x≥0).------------4分
(2)设B产品投入x万元,A产品投入(18-x)万元,该企业可获总利润为y万元.
则y=(18-x)+2,0≤x≤18-------------------------5分
令=t,t∈[0,3],----------------6分
则y=(-t 2+8t+18)=-(t-4)2+ .-----------------8分
所以当t=4时,ymax==8.5,-------------------------9分
此时x=16,18-x=2.
所以当A,B两种产品分别投入2万元、16万元时,可使该企业获得最大利润,
约为8.5万元.--------------------------12分
21.解:(1)由题意知,解得
此时符合 , 故 - --------------4分
(2)函数在(-1,1)为单调函数.证明如下:
任取,则
,
即
故在(-1,1)上为增函数 ---------------8分
(3)由(1)、(2)可得
则
解得:
所以,原不等式的解集为 --------------12分
22.解: (1)∵幂函数f(x)=(k2+k﹣1)x(2﹣k)(1+k)在(0,+∞)上单调递增,
可得(2﹣k)(1+k)>0,解得﹣1<k<2,
又k2+k﹣1=1,可得k=﹣2或1,
即有k=1,幂函数f(x)=x2; ---------------2分
(2)由(1)可知:g(x)=﹣mx2+(2m﹣1)x+1,
当m=0时,g(x)=1﹣x在[0,1]递减,可得g(0)取得最大值,且为1,不成立;
当m<0时,g(x)图象开口向上,最大值在g(0)或g(1)处取得,
而g(0)=1,则g(1)=5,即为m=5,不成立;
当m>0,即﹣m<0,g(x)=﹣m(x﹣)2+.
①当≤0,m>0时,解得0<m≤,
则g(x)在[0,1]上单调递减,因此在x=0处取得最大值,
而g(0)=1≠5不符合要求,应舍去;
②当≥1,m>0时,解得m不存在;
③当0<<1,m>0时,解得m>,
则g(x)在x=处取得最小值,最大值在x=0或1处取得,
而g(0)=1不符合要求;由g(1)=5,即m=5,满足m的范围.
综上可知:满足条件的m存在且m=5. ---------------7分
(3)由(1)知
令,显然在递增,. --------------9分
故原问题转化到不等式对任意的恒成立,
即不等式对任意的恒成立.
令 由双勾函数知在递减,递增
,故 ---------------12分
数 学 试 卷
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
1.把集合用列举法表示为( )
A.{,} B.{x|或}
C.{} D.{}
2.下列对应关系:
①,,的平方根;
②,的倒数;
③,;
④,,.
其中是到的映射的是( )
A. ①③ B.②④ C. ②③ D. ③④
3.已知,则( )
A.2 B.3 C.4 D.5
4. 已知集合,集合,则与的关系是( )
A. B. C. D. 且
5.已知集合 则( )
A.[2,3] B. C.[1,2) D.
6.下列函数中,在上为增函数的是( )
A. B. C. D.
7.如图的曲线是幂函数在第一象限内的图象,已知分别取,2四个值,相应曲线、、、的依次为( )
A. B.
C. D.
8.已知是定义在上是减函数,则的取值范围是( )
A. B. C. D.
9.已知函数,且,则下列不等式中成立的是( )
A. B.
C. D.
10.函数在单调递减,且为奇函数.若,则满足的的取值范围是( )
A. B. C. D.
11.若、是关于的方程()的两个实根,则 的最大值等于( )
A.6 B. C.18 D.19
12.若函数是偶函数,则的最小值为( )
A. B. C. D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分。将答案填在答题卡上的相应位置)
13.设集合,.若,则 .(用列举法表示)
14.已知集合,则 .
15.已知函数的值域为,则实数的取值范围为
16.给出定义:若 (其中为整数),则叫做离实数最近的整数,记作.在此基础上给出下列关于函数的四个结论:
①函数的定义域为,值域为;
②函数的图象关于直线对称;
③函数是偶函数;④函数在上是增函数.
其中正确的结论的序号是________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
17. (本小题满分10分)
设函数的定义域为集合,已知集合,,全集为.
(I)求;
(II)若,求实数的取值范围.
18.(本小题满分12分)
已知集合,.
(Ⅰ) 当时,集合的元素中整数有多少个?
(Ⅱ)若,求实数的取值范围.
19.(本小题满分12分)
已知函数是定义在R上的偶函数,已知当时, .
(1)求函数的解析式;
(2)画出函数的图象,并写出函数的单调递增区间;
(3)试确定方程的解个数.
20.(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
① ②
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
21. (本小题满分12分)
已知函数是定义在上的奇函数,且
(1)确定函数的解析式;
(2)判断函数在定义域内的单调性,并用定义证明;
(3解不等式.
22. (本小题满分12分)
已知幂函数在上单调递增.
(1)求实数的值,并写出函数的解析式;
(2)对于(1)中的函数,试判断是否存在整数,使函数在上的最大值为,若存在,求出的值;若不存在,请说明理由;
(3)设函数,若不等式对任意的恒成立,求实数的取值范围.
南康中学2018~2019学年度第一学期高一第一次大考
数学参考答案
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
A
C
B
B
B
A
C
D
C
C
二、填空题(本大题共4小题,每小题5分,共20分。将答案填在答题卡上的相应位置)
13. 14. 15. 16. ①②③
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤 )
; ---------------5分
即实数的取值范围为. ---------------10分
注:第(1)问5分,第二问7分.
19.(1)当x>0时,-x<0 ∴f(-x)=(-x)2+4(-x)+3=x2-4x+3
∴f(x)为R上的偶函数 ∴f(-x)= f(x)= x2-4x+3
∴ --------------4分
(2)的图像略, --------------6分
f(x)单调增区间为和. ---------------8分
(3)有图知或,从而知方程有10个解. ---------------12分
20.(1)根据题意可设,。---------2分
则f(x)=0.25x(x≥0),g(x)=2 (x≥0).------------4分
(2)设B产品投入x万元,A产品投入(18-x)万元,该企业可获总利润为y万元.
则y=(18-x)+2,0≤x≤18-------------------------5分
令=t,t∈[0,3],----------------6分
则y=(-t 2+8t+18)=-(t-4)2+ .-----------------8分
所以当t=4时,ymax==8.5,-------------------------9分
此时x=16,18-x=2.
所以当A,B两种产品分别投入2万元、16万元时,可使该企业获得最大利润,
约为8.5万元.--------------------------12分
21.解:(1)由题意知,解得
此时符合 , 故 - --------------4分
(2)函数在(-1,1)为单调函数.证明如下:
任取,则
,
即
故在(-1,1)上为增函数 ---------------8分
(3)由(1)、(2)可得
则
解得:
所以,原不等式的解集为 --------------12分
22.解: (1)∵幂函数f(x)=(k2+k﹣1)x(2﹣k)(1+k)在(0,+∞)上单调递增,
可得(2﹣k)(1+k)>0,解得﹣1<k<2,
又k2+k﹣1=1,可得k=﹣2或1,
即有k=1,幂函数f(x)=x2; ---------------2分
(2)由(1)可知:g(x)=﹣mx2+(2m﹣1)x+1,
当m=0时,g(x)=1﹣x在[0,1]递减,可得g(0)取得最大值,且为1,不成立;
当m<0时,g(x)图象开口向上,最大值在g(0)或g(1)处取得,
而g(0)=1,则g(1)=5,即为m=5,不成立;
当m>0,即﹣m<0,g(x)=﹣m(x﹣)2+.
①当≤0,m>0时,解得0<m≤,
则g(x)在[0,1]上单调递减,因此在x=0处取得最大值,
而g(0)=1≠5不符合要求,应舍去;
②当≥1,m>0时,解得m不存在;
③当0<<1,m>0时,解得m>,
则g(x)在x=处取得最小值,最大值在x=0或1处取得,
而g(0)=1不符合要求;由g(1)=5,即m=5,满足m的范围.
综上可知:满足条件的m存在且m=5. ---------------7分
(3)由(1)知
令,显然在递增,. --------------9分
故原问题转化到不等式对任意的恒成立,
即不等式对任意的恒成立.
令 由双勾函数知在递减,递增
,故 ---------------12分
同课章节目录
