24.3 正多边形和圆课时作业
图片预览


文档简介
24.3 正多边形和圆课时作业
姓名:__________班级:__________考号:__________
、选择题
1.正三角形的外接圆半径与内切圆的半径之比是( )
A.1:2 B.1: C. :1 D.2:1
2.已知某个正多边形的内切圆的半径是 ,外接圆的半径是2,则此正多边形的边数是( )
A.八 B.六 C.四 D.三
3.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
4.顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
A.△ACE是等边三角形
B.既是轴对称图形也是中心对称图形
C.连接AD,则AD分别平分∠EAC与∠EDC
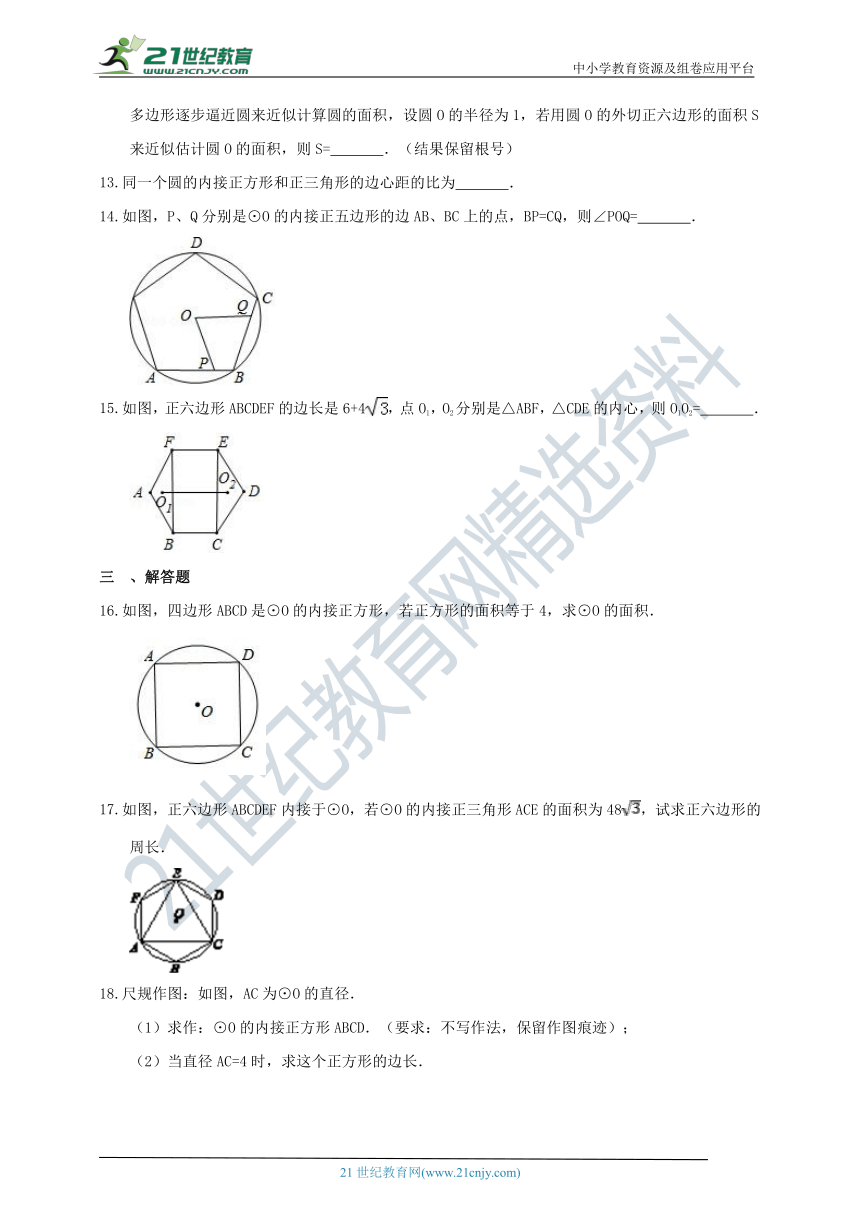
D.图中一共能画出3条对称轴
5.下列正多边形中,中心角等于内角的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
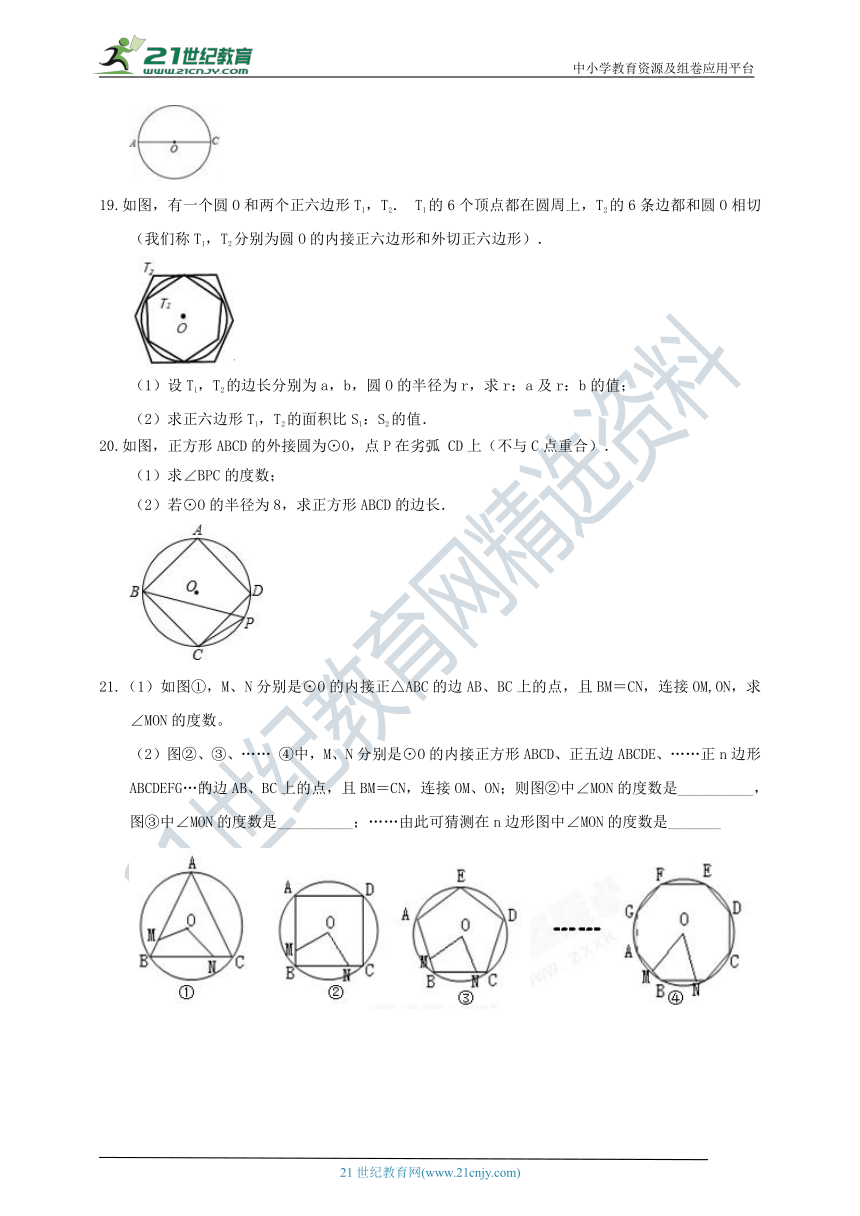
6.半径为8cm的圆的内接正三角形的边长为( )
A.8cm B.4cm C.8cm D.4cm
7.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边
重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4 B.1.1 C.0.8 D.0.5
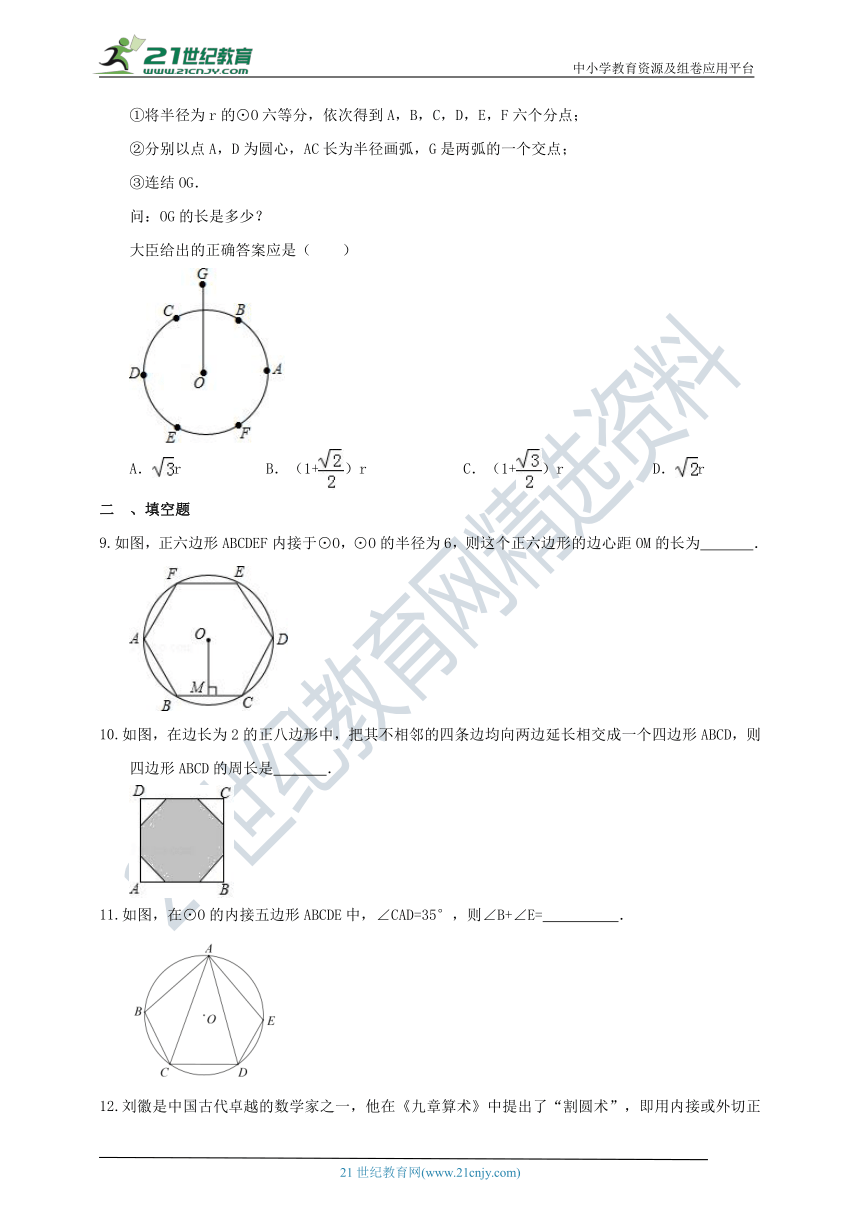
8.尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A.r B.(1+)r C.(1+)r D.r
、填空题
9.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为 .
10.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
11.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= .
12.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积S来近似估计圆O的面积,则S= .(结果保留根号)
13.同一个圆的内接正方形和正三角形的边心距的比为 .
14.如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .
15.如图,正六边形ABCDEF的边长是6+4,点O1,O2分别是△ABF,△CDE的内心,则O1O2= .
、解答题
16.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48,试求正六边形的周长.
18.尺规作图:如图,AC为⊙O的直径.
(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);
(2)当直径AC=4时,求这个正方形的边长.
19.如图,有一个圆O和两个正六边形T1,T2. T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;
(2)求正六边形T1,T2的面积比S1:S2的值.
20.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
21.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数。
(2)图②、③、…… ④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
答案解析
、选择题
1.【考点】正多边形和圆
【分析】先作出图形,根据等边三角形的性质确定它的内切圆和外接圆的圆心;通过特殊角进行计算,用内切圆半径来表示外接圆半径,最后求出比值即可.
解:如图,
△ABC是等边三角形,AD是高.点O是其外接圆的圆心,由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴OA:OD=2:1.
故选D.
2.【考点】正多边形和圆
【分析】根据正多边形的内切圆的半径,外接圆的半径,正多边形的边长的一半构成直角三角形,可得出正多边形的中心角,从而得出正多边形的边数即可.
解:根据勾股定理得:=1,
∴正多边形的边长为2,
∴正多边形的中心角为60°,
∴此正多边形是正六边形,
故选B.
3.【考点】正多边形和圆
【分析】解题的关键要记住正六边形的特点,它被半径分成六个全等的等边三角形.
解:连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2 ,高为3,
因而等边三角形的面积是3 ,
∴正六边形的面积=18 ,
故选C.
4.【考点】正多边形和圆
【分析】根据正多边形的性质和轴对称图形与中心对称图形的定义解答.解: A.∵多边形ABCDEF是正六边形,
∴△ACE是等边三角形,故本选项正确;
B.∵△ACE是等边三角形,∴是轴对称图形,不是中心对称图形,故本选项错误;
C.∵△ACE是等边三角形,∴连接AD,则AD分别平分∠EAC与∠EDC,故本选项正确;
D.∵△ACE是等边三角形,∴图中一共能画3条对称轴,故本选项正确.
故选B.
5.【考点】正多边形和圆
【分析】设正边形的边数是n,根据内角根据中心角等于内角,就可以得到一个关于n的方程,解方程就可以解得n的值
解:设正边形的边数是n.
根据题意得:180-,
解得:n=4.
故选B.
6.【考点】正多边形和圆
【分析】欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长.
解:如图所示:
∵半径为8cm的圆的内接正三角形,
∴在Rt△BOD中,OB=8cm,∠OBD=30°,
∴BD=cos30°×OB= ×8=4 (cm),
∵BD=CD,
∴BC=2BD=8 cm.
故它的内接正三角形的边长为8 cm.
故选:A.
7.【考点】正多边形和圆;旋转的性质.
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于2﹣小于等于1,由此即可判断.
解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣小于等于1,
故选C.
8.【考点】正多边形和圆;作图—复杂作图
【分析】如图连接CD,AC,DG,AG.在直角三角形即可解决问题;
解:如图连接CD,AC,DG,AG.
∵AD是⊙O直径,
∴∠ACD=90°,
在Rt△ACD中,AD=2r,∠DAC=30°,
∴AC=r,
∵DG=AG=CA,OD=OA,
∴OG⊥AD,
∴∠GOA=90°,
∴OG===r,
故选:D.
【点评】本题考查作图﹣复杂作图,正多边形与圆的关系,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
、填空题
9.【考点】正多边形和圆.
【分析】根据正六边形的性质求出∠BOM,利用余弦的定义计算即可.
解:连接OB,
∵六边形ABCDEF是⊙O内接正六边形,
∴∠BOM==30°,
∴OM=OB?cos∠BOM=6×=3;
故答案为:3.
10.【考点】正多边形和圆.
【分析】根据题意可知形成的四个小的直角三角形全等,并且四个都是等腰直角三角形,从而可以求得四边形ABCD一边的长,从而可以求得四边形ABCD的周长.
解:由题意可得,
AD=2+×2=2+2,
∴四边形ABCD的周长是:4×(2+2)=8+8,
故答案为:8+8.
11.【考点】圆内接四边形的性质,圆周角定理
【分析】连接CE,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD,然后求解即可.
解:如图,连接CE,
∵五边形ABCDE是圆内接五边形, ∴四边形ABCE是圆内接四边形, ∴∠B+∠AEC=180°, ∵∠CED=∠CAD=35°, ∴∠B+∠E=180°+35°=215°. 故答案为:215°.
【点评】本题考查了圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题的关键.
12.【考点】数学常识;正多边形和圆
【分析】根据正多边形的定义可得出△ABO为等边三角形,根据等边三角形的性质结合OM的长度可求出AB的长度,再利用三角形的面积公式即可求出S的值.
解:依照题意画出图象,如图所示.
∵六边形ABCDEF为正六边形,
∴△ABO为等边三角形,
∵⊙O的半径为1,
∴OM=1,
∴BM=AM=,
∴AB=,
∴S=6S△ABO=6×××1=2.
故答案为:2.
【点评】本题考查了正多边形和圆、三角形的面积以及数学常识,根据等边三角形的性质求出正六边形的边长是解题的关键.
13.【考点】正多边形与圆,解直角三角形,等边三角形的性质,正方形的性质
【分析】先化成同一个圆的内接正方形和内接正三角形,设⊙O的半径为R,求出正方形的边心距和正三角形的边心距,再求出比值即可.
解:设⊙O的半径为r,⊙O的内接正方形ABCD,如图,
过O作OQ⊥BC于Q,连接OB、OC,即OQ为正方形ABCD的边心距,
∵四边形BACD是正方形,⊙O是正方形ABCD的外接圆,
∴O为正方形ABCD的中心,
∴∠BOC=90°,
∵OQ⊥BC,OB=CO,
∴QC=BQ,∠COQ=∠BOQ=45°,
∴OQ=OC×cos45°=R;
设⊙O的内接正△EFG,如图,
过O作OH⊥FG于H,连接OG,即OH为正△EFG的边心距,
∵正△EFG是⊙O的外接圆,
∴∠OGF=∠EGF=30°,
∴OH=OG×sin30°=R,
∴OQ:OH=(R):(R)=:1,
故答案为::1.
【点评】本题考查了正多边形与圆、解直角三角形,等边三角形的性质、正方形的性质解直角三角形等知识点,能综合运用知识点进行推理和计算是解此题的关键.
14.【考点】正多边形和圆.
【分析】连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.
解:连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
15.【考点】正多边形和圆
【分析】设△AFB的内切圆的半径为r,过A作AM⊥BF于M,连接O1F、O1A、O1B,解直角三角形求出AM、FM、BM,根据三角形的面积求出r,即可求出答案.
解:过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A==120°,AF=AB,
∴∠AFB=∠ABF=(180°﹣120°)=30°,
∴△AFB边BF上的高AM=AF=(6+4)=3+2,FM=BM=AM=3+6,
∴BF=3+6+3+6=12+6,
设△AFB的内切圆的半径为r,
∵S△AFB=S+S+S,
∴×(3+2)×(3+6)=×r+×r+×(12+6)×r,
解得:r=,
即O1M=r=,
∴O1O2=2×+6+4=9+4,
故答案为:9+4.
、解答题
16.【考点】正多边形和圆
【分析】根据正方形的面积公式求得半径,然后根据圆的面积公式求解.
解:∵正方形的面积等于4,
∴正方形的边长AB=2,
则半径是2×=,
∴⊙O的面积=π()2=2π.
【点睛】本题考查了正多边形的计算,根据正方形的面积求得半径是关键.
17.【考点】正多边形和圆
【分析】连接OA,作OH⊥AC于点H,则∠OAH=30°. 连接OA,作OH⊥AC于点H,则∠OAH=30°. 由△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R,可求出周长.
解: 如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,AH=
=
而△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
【点睛】本题考核知识点:正多边形和圆.解题关键点:结合勾股定理求出边长.
18.【考点】正多边形和圆
【分析】(1)过点O作出直径AC的垂线,进而得出答案;
(2)利用正方形的性质结合勾股定理得出正方形ABCD的边长.
解:(1)如图所示:
(2)∵直径AC=4,∴OA=OB=2.∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,∴AB==.
【点睛】此题主要考查了复杂作图以及正多边形和圆,正确掌握正方形的性质是解题的关键.
19.【考点】正多边形和圆
【分析】根据题意画出图形,连接OE、OG,OF,由正六边形T1,得到∠EOF为60°,从而得到△EOF为等边三角形,即a=r,故得到a:r=1:1;在Rt△EOG中,由OG为角平分线,得到∠EOG=30°,利用特殊角的三角函数可求出OE及OG的长,即为r:b的比值,然后求出a:b的比值,根据正六边形T1,T2相似,其面积之比等于边长之比的平方,即可求出面积之比.
解:(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.
所以r:a=1:1;
连接圆心O和T2相邻的两个顶点,得以圆O半径为高的正三角形,
所以r:b=AO:BO=sin60°=:2;
(2)T1:T2的边长比是:2,所以S1:S2=(a:b)2=3:4.
【点睛】本题考查的是正多边形和圆及特殊角的三角函数值,解答此题的关键是根据题意画出图形,再由三角函数的定义及特殊角的三角函数值求解.
20.【考点】正多边形和圆
【分析】(1)连接OB,OC,由正方形的性质知,△BOC是等腰直角三角形,根据∠BOC=90°,由圆周角定理可以求出; (2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
解: :(1)连接OB,OC,
∵四边形ABCD为正方形,
∴∠BOC=90°,ssssss
∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=
∴BC=2BE=2×
21.【考点】正多边形和圆, 圆周角定理
【分析】(1)先分别连接OB、OC,可求出∠BOM=∠NOC,故∠MON=∠BOC,再由圆周角定理即可求出∠BOC=120°;(2)同(1)即可解答;(3)由(1)、(2)找出规律,即可解答.
解:分别连接OB、OC,
(1)∵AB=AC,
∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,
∴△OMB≌△ONC,
∴∠BOM=∠NOC,
∵∠BAC=60°,
∴∠BOC=120°;
∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON==120°;在(2)中,∠MON==90°;在(3)中∠MON=5=72°…,故当n时,∠MON=.
【睛】本题考查的是正多边形和圆,根据题意作出辅助线,构造出全等三角形是解答此题的关键.
姓名:__________班级:__________考号:__________
、选择题
1.正三角形的外接圆半径与内切圆的半径之比是( )
A.1:2 B.1: C. :1 D.2:1
2.已知某个正多边形的内切圆的半径是 ,外接圆的半径是2,则此正多边形的边数是( )
A.八 B.六 C.四 D.三
3.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
4.顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
A.△ACE是等边三角形
B.既是轴对称图形也是中心对称图形
C.连接AD,则AD分别平分∠EAC与∠EDC
D.图中一共能画出3条对称轴
5.下列正多边形中,中心角等于内角的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
6.半径为8cm的圆的内接正三角形的边长为( )
A.8cm B.4cm C.8cm D.4cm
7.已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边
重合,如图所示,按下列步骤操作:
将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4 B.1.1 C.0.8 D.0.5
8.尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A.r B.(1+)r C.(1+)r D.r
、填空题
9.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为 .
10.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
11.如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E= .
12.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积S来近似估计圆O的面积,则S= .(结果保留根号)
13.同一个圆的内接正方形和正三角形的边心距的比为 .
14.如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .
15.如图,正六边形ABCDEF的边长是6+4,点O1,O2分别是△ABF,△CDE的内心,则O1O2= .
、解答题
16.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48,试求正六边形的周长.
18.尺规作图:如图,AC为⊙O的直径.
(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);
(2)当直径AC=4时,求这个正方形的边长.
19.如图,有一个圆O和两个正六边形T1,T2. T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;
(2)求正六边形T1,T2的面积比S1:S2的值.
20.如图,正方形ABCD的外接圆为⊙O,点P在劣弧 CD上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
21.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数。
(2)图②、③、…… ④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
答案解析
、选择题
1.【考点】正多边形和圆
【分析】先作出图形,根据等边三角形的性质确定它的内切圆和外接圆的圆心;通过特殊角进行计算,用内切圆半径来表示外接圆半径,最后求出比值即可.
解:如图,
△ABC是等边三角形,AD是高.点O是其外接圆的圆心,由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴OA:OD=2:1.
故选D.
2.【考点】正多边形和圆
【分析】根据正多边形的内切圆的半径,外接圆的半径,正多边形的边长的一半构成直角三角形,可得出正多边形的中心角,从而得出正多边形的边数即可.
解:根据勾股定理得:=1,
∴正多边形的边长为2,
∴正多边形的中心角为60°,
∴此正多边形是正六边形,
故选B.
3.【考点】正多边形和圆
【分析】解题的关键要记住正六边形的特点,它被半径分成六个全等的等边三角形.
解:连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是2 ,高为3,
因而等边三角形的面积是3 ,
∴正六边形的面积=18 ,
故选C.
4.【考点】正多边形和圆
【分析】根据正多边形的性质和轴对称图形与中心对称图形的定义解答.解: A.∵多边形ABCDEF是正六边形,
∴△ACE是等边三角形,故本选项正确;
B.∵△ACE是等边三角形,∴是轴对称图形,不是中心对称图形,故本选项错误;
C.∵△ACE是等边三角形,∴连接AD,则AD分别平分∠EAC与∠EDC,故本选项正确;
D.∵△ACE是等边三角形,∴图中一共能画3条对称轴,故本选项正确.
故选B.
5.【考点】正多边形和圆
【分析】设正边形的边数是n,根据内角根据中心角等于内角,就可以得到一个关于n的方程,解方程就可以解得n的值
解:设正边形的边数是n.
根据题意得:180-,
解得:n=4.
故选B.
6.【考点】正多边形和圆
【分析】欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长.
解:如图所示:
∵半径为8cm的圆的内接正三角形,
∴在Rt△BOD中,OB=8cm,∠OBD=30°,
∴BD=cos30°×OB= ×8=4 (cm),
∵BD=CD,
∴BC=2BD=8 cm.
故它的内接正三角形的边长为8 cm.
故选:A.
7.【考点】正多边形和圆;旋转的性质.
【分析】如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,观察图象可知点B,M间的距离大于等于2﹣小于等于1,由此即可判断.
解:如图,在这样连续6次旋转的过程中,点M的运动轨迹是图中的红线,
观察图象可知点B,M间的距离大于等于2﹣小于等于1,
故选C.
8.【考点】正多边形和圆;作图—复杂作图
【分析】如图连接CD,AC,DG,AG.在直角三角形即可解决问题;
解:如图连接CD,AC,DG,AG.
∵AD是⊙O直径,
∴∠ACD=90°,
在Rt△ACD中,AD=2r,∠DAC=30°,
∴AC=r,
∵DG=AG=CA,OD=OA,
∴OG⊥AD,
∴∠GOA=90°,
∴OG===r,
故选:D.
【点评】本题考查作图﹣复杂作图,正多边形与圆的关系,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
、填空题
9.【考点】正多边形和圆.
【分析】根据正六边形的性质求出∠BOM,利用余弦的定义计算即可.
解:连接OB,
∵六边形ABCDEF是⊙O内接正六边形,
∴∠BOM==30°,
∴OM=OB?cos∠BOM=6×=3;
故答案为:3.
10.【考点】正多边形和圆.
【分析】根据题意可知形成的四个小的直角三角形全等,并且四个都是等腰直角三角形,从而可以求得四边形ABCD一边的长,从而可以求得四边形ABCD的周长.
解:由题意可得,
AD=2+×2=2+2,
∴四边形ABCD的周长是:4×(2+2)=8+8,
故答案为:8+8.
11.【考点】圆内接四边形的性质,圆周角定理
【分析】连接CE,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD,然后求解即可.
解:如图,连接CE,
∵五边形ABCDE是圆内接五边形, ∴四边形ABCE是圆内接四边形, ∴∠B+∠AEC=180°, ∵∠CED=∠CAD=35°, ∴∠B+∠E=180°+35°=215°. 故答案为:215°.
【点评】本题考查了圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题的关键.
12.【考点】数学常识;正多边形和圆
【分析】根据正多边形的定义可得出△ABO为等边三角形,根据等边三角形的性质结合OM的长度可求出AB的长度,再利用三角形的面积公式即可求出S的值.
解:依照题意画出图象,如图所示.
∵六边形ABCDEF为正六边形,
∴△ABO为等边三角形,
∵⊙O的半径为1,
∴OM=1,
∴BM=AM=,
∴AB=,
∴S=6S△ABO=6×××1=2.
故答案为:2.
【点评】本题考查了正多边形和圆、三角形的面积以及数学常识,根据等边三角形的性质求出正六边形的边长是解题的关键.
13.【考点】正多边形与圆,解直角三角形,等边三角形的性质,正方形的性质
【分析】先化成同一个圆的内接正方形和内接正三角形,设⊙O的半径为R,求出正方形的边心距和正三角形的边心距,再求出比值即可.
解:设⊙O的半径为r,⊙O的内接正方形ABCD,如图,
过O作OQ⊥BC于Q,连接OB、OC,即OQ为正方形ABCD的边心距,
∵四边形BACD是正方形,⊙O是正方形ABCD的外接圆,
∴O为正方形ABCD的中心,
∴∠BOC=90°,
∵OQ⊥BC,OB=CO,
∴QC=BQ,∠COQ=∠BOQ=45°,
∴OQ=OC×cos45°=R;
设⊙O的内接正△EFG,如图,
过O作OH⊥FG于H,连接OG,即OH为正△EFG的边心距,
∵正△EFG是⊙O的外接圆,
∴∠OGF=∠EGF=30°,
∴OH=OG×sin30°=R,
∴OQ:OH=(R):(R)=:1,
故答案为::1.
【点评】本题考查了正多边形与圆、解直角三角形,等边三角形的性质、正方形的性质解直角三角形等知识点,能综合运用知识点进行推理和计算是解此题的关键.
14.【考点】正多边形和圆.
【分析】连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.
解:连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
15.【考点】正多边形和圆
【分析】设△AFB的内切圆的半径为r,过A作AM⊥BF于M,连接O1F、O1A、O1B,解直角三角形求出AM、FM、BM,根据三角形的面积求出r,即可求出答案.
解:过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A==120°,AF=AB,
∴∠AFB=∠ABF=(180°﹣120°)=30°,
∴△AFB边BF上的高AM=AF=(6+4)=3+2,FM=BM=AM=3+6,
∴BF=3+6+3+6=12+6,
设△AFB的内切圆的半径为r,
∵S△AFB=S+S+S,
∴×(3+2)×(3+6)=×r+×r+×(12+6)×r,
解得:r=,
即O1M=r=,
∴O1O2=2×+6+4=9+4,
故答案为:9+4.
、解答题
16.【考点】正多边形和圆
【分析】根据正方形的面积公式求得半径,然后根据圆的面积公式求解.
解:∵正方形的面积等于4,
∴正方形的边长AB=2,
则半径是2×=,
∴⊙O的面积=π()2=2π.
【点睛】本题考查了正多边形的计算,根据正方形的面积求得半径是关键.
17.【考点】正多边形和圆
【分析】连接OA,作OH⊥AC于点H,则∠OAH=30°. 连接OA,作OH⊥AC于点H,则∠OAH=30°. 由△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R,可求出周长.
解: 如图,连接OA,作OH⊥AC于点H,则∠OAH=30°.
在Rt△OAH中,设OA=R,则OH=R,AH=
=
而△ACE的面积是△OAH面积的6倍,即6×× R×R=48,解得R=8,
即正六边形的边长为8,所以正六边形的周长为48.
【点睛】本题考核知识点:正多边形和圆.解题关键点:结合勾股定理求出边长.
18.【考点】正多边形和圆
【分析】(1)过点O作出直径AC的垂线,进而得出答案;
(2)利用正方形的性质结合勾股定理得出正方形ABCD的边长.
解:(1)如图所示:
(2)∵直径AC=4,∴OA=OB=2.∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,∴AB==.
【点睛】此题主要考查了复杂作图以及正多边形和圆,正确掌握正方形的性质是解题的关键.
19.【考点】正多边形和圆
【分析】根据题意画出图形,连接OE、OG,OF,由正六边形T1,得到∠EOF为60°,从而得到△EOF为等边三角形,即a=r,故得到a:r=1:1;在Rt△EOG中,由OG为角平分线,得到∠EOG=30°,利用特殊角的三角函数可求出OE及OG的长,即为r:b的比值,然后求出a:b的比值,根据正六边形T1,T2相似,其面积之比等于边长之比的平方,即可求出面积之比.
解:(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.
所以r:a=1:1;
连接圆心O和T2相邻的两个顶点,得以圆O半径为高的正三角形,
所以r:b=AO:BO=sin60°=:2;
(2)T1:T2的边长比是:2,所以S1:S2=(a:b)2=3:4.
【点睛】本题考查的是正多边形和圆及特殊角的三角函数值,解答此题的关键是根据题意画出图形,再由三角函数的定义及特殊角的三角函数值求解.
20.【考点】正多边形和圆
【分析】(1)连接OB,OC,由正方形的性质知,△BOC是等腰直角三角形,根据∠BOC=90°,由圆周角定理可以求出; (2)过点O作OE⊥BC于点E,由等腰直角三角形的性质可知OE=BE,由垂径定理可知BC=2BE,故可得出结论.
解: :(1)连接OB,OC,
∵四边形ABCD为正方形,
∴∠BOC=90°,ssssss
∴∠P=∠BOC=45°;
(2)过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,
∴OE=BE,
∵OE2+BE2=OB2,
∴BE=
∴BC=2BE=2×
21.【考点】正多边形和圆, 圆周角定理
【分析】(1)先分别连接OB、OC,可求出∠BOM=∠NOC,故∠MON=∠BOC,再由圆周角定理即可求出∠BOC=120°;(2)同(1)即可解答;(3)由(1)、(2)找出规律,即可解答.
解:分别连接OB、OC,
(1)∵AB=AC,
∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,
∴△OMB≌△ONC,
∴∠BOM=∠NOC,
∵∠BAC=60°,
∴∠BOC=120°;
∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON==120°;在(2)中,∠MON==90°;在(3)中∠MON=5=72°…,故当n时,∠MON=.
【睛】本题考查的是正多边形和圆,根据题意作出辅助线,构造出全等三角形是解答此题的关键.
同课章节目录
