《总复习——图形与几何》课件 (共15张PPT)
文档属性
| 名称 | 《总复习——图形与几何》课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-19 20:52:12 | ||
图片预览






文档简介
课件15张PPT。总复习
——图形与几何对称、平移与旋转轴对称图形1、轴对称图形和对称轴:
将图形沿着一条直线对折,如果折痕两侧的部分能够完全重合,这样的图形叫作轴对称图形。折痕所在的这条直线叫作它的对称轴。
2、画轴对称图形另一半的办法:
①找出所给图形的关键点。
②数出或量出图形关键点到对称轴的距离。
③在对称轴的另一侧找出关键点的对称点。
④按照所给图形的形状连接各点,画出所给图形的另一半。对称、平移与旋转图形的平移1、平移的特点:
物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生变化。
2、在方格纸上画平移图形的方法:
①找出图形的关键点(或关键线段)。
②以关键点(或关键线段)为参照点(或参照线段),数出平移的格数。
③按指定方向和格数把参照点(或参照线段)平移到新位置,描出各点(或画出线段)。
④把各点按原图形状顺次连接,就得到平移后的图形。对称、平移与旋转图形的旋转1、旋转的意义:
物体绕着某一点(或轴)运动,这种运动现象叫作旋转。
2、旋转的方向:
与时针旋转方向相同的是顺时针旋转;与时针旋转方向相反的是逆时针旋转。
3、旋转的三要素:
旋转中心、旋转方向和旋转角度。对称、平移与旋转图形的旋转4、旋转的性质:
图形绕某一点旋转一定的度数,图形中的对应点、对应线段都旋转相应的角度,相对应的点到旋转点的距离相等。
5、旋转的特征:
物体或图形旋转后,形状、大小都没有发生变化,只是方向和位置改变了。对称、平移与旋转图形的旋转6、运用旋转设计图案的方法:
①选好基本图形。
②根据所选的基本图形确定旋转点。
③确定好旋转角度。
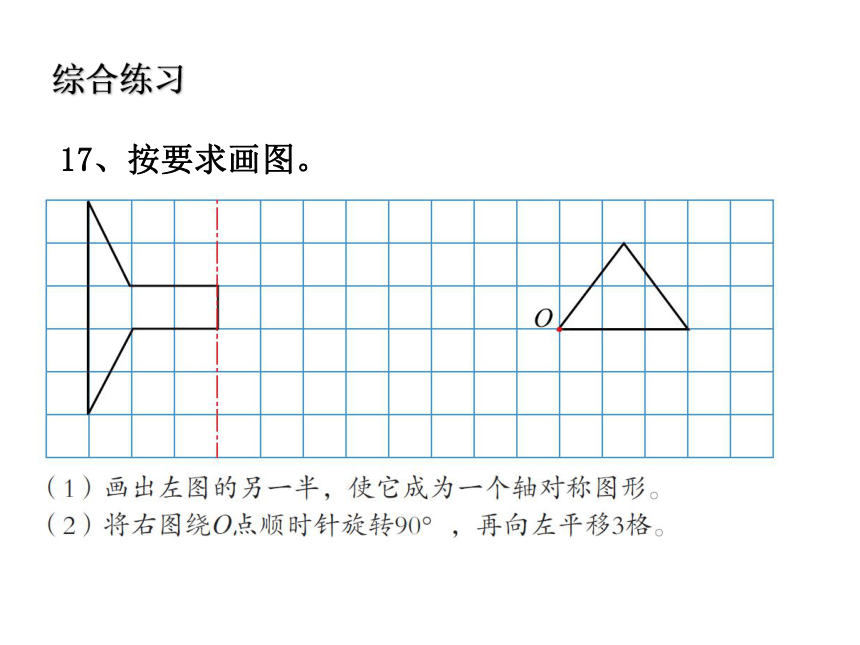
④画出旋转后的基本图形。综合练习17、按要求画图。多边形的面积平行四边形面积的计算1、平行四边形:
两组对边分别平行的四边形叫作平行四边形。
2、平行四边形的特征:
平行四边形的对边平行且相等,对角相等。
3、平行四边形的面积=底×高,用字母表示为S=ah。三角形面积的计算三角形的面积=底×高÷2,用字母表示为S=ah÷2。多边形的面积梯形面积的计算1、梯形的意义:
只有一组对边平行的四边形叫作梯形。
2、等腰梯形:
两腰相等的梯形叫作等腰梯形。
3、直角梯形:
只有一条腰垂直于底边的梯形叫作直角梯形。
4、梯形的面积=(上底+下底)×高÷2,用字母表示为:S=(a+b)h÷2。多边形的面积组合图形面积的计算把组合图形分成几个简单图形,分别求出每个简单图形的面积,再把各部分的面积加起来;或者将组合图形补成一个简单图形,求出它的面积,再将增补图形的面积减去。土地面积1、公顷、平方千米是常用的土地面积单位。
2、1公顷=10000平方米
1平方千米=100公顷=1000000平方米综合练习13.计算下面个图形的面积。(单位:厘米)3×2.2÷2=3.3(平方厘米)7×3.8=26.6(平方厘米)综合练习13.计算下面个图形的面积。(单位:厘米) (20+60)×20÷2
=80×20÷2
=800(平方厘米) 65×50+50×20÷2
=3250+500
=3750(平方厘米)综合练习15.CBC综合练习14.哪种说法正确?(单位:分米)√回顾反思
——图形与几何对称、平移与旋转轴对称图形1、轴对称图形和对称轴:
将图形沿着一条直线对折,如果折痕两侧的部分能够完全重合,这样的图形叫作轴对称图形。折痕所在的这条直线叫作它的对称轴。
2、画轴对称图形另一半的办法:
①找出所给图形的关键点。
②数出或量出图形关键点到对称轴的距离。
③在对称轴的另一侧找出关键点的对称点。
④按照所给图形的形状连接各点,画出所给图形的另一半。对称、平移与旋转图形的平移1、平移的特点:
物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生变化。
2、在方格纸上画平移图形的方法:
①找出图形的关键点(或关键线段)。
②以关键点(或关键线段)为参照点(或参照线段),数出平移的格数。
③按指定方向和格数把参照点(或参照线段)平移到新位置,描出各点(或画出线段)。
④把各点按原图形状顺次连接,就得到平移后的图形。对称、平移与旋转图形的旋转1、旋转的意义:
物体绕着某一点(或轴)运动,这种运动现象叫作旋转。
2、旋转的方向:
与时针旋转方向相同的是顺时针旋转;与时针旋转方向相反的是逆时针旋转。
3、旋转的三要素:
旋转中心、旋转方向和旋转角度。对称、平移与旋转图形的旋转4、旋转的性质:
图形绕某一点旋转一定的度数,图形中的对应点、对应线段都旋转相应的角度,相对应的点到旋转点的距离相等。
5、旋转的特征:
物体或图形旋转后,形状、大小都没有发生变化,只是方向和位置改变了。对称、平移与旋转图形的旋转6、运用旋转设计图案的方法:
①选好基本图形。
②根据所选的基本图形确定旋转点。
③确定好旋转角度。
④画出旋转后的基本图形。综合练习17、按要求画图。多边形的面积平行四边形面积的计算1、平行四边形:
两组对边分别平行的四边形叫作平行四边形。
2、平行四边形的特征:
平行四边形的对边平行且相等,对角相等。
3、平行四边形的面积=底×高,用字母表示为S=ah。三角形面积的计算三角形的面积=底×高÷2,用字母表示为S=ah÷2。多边形的面积梯形面积的计算1、梯形的意义:
只有一组对边平行的四边形叫作梯形。
2、等腰梯形:
两腰相等的梯形叫作等腰梯形。
3、直角梯形:
只有一条腰垂直于底边的梯形叫作直角梯形。
4、梯形的面积=(上底+下底)×高÷2,用字母表示为:S=(a+b)h÷2。多边形的面积组合图形面积的计算把组合图形分成几个简单图形,分别求出每个简单图形的面积,再把各部分的面积加起来;或者将组合图形补成一个简单图形,求出它的面积,再将增补图形的面积减去。土地面积1、公顷、平方千米是常用的土地面积单位。
2、1公顷=10000平方米
1平方千米=100公顷=1000000平方米综合练习13.计算下面个图形的面积。(单位:厘米)3×2.2÷2=3.3(平方厘米)7×3.8=26.6(平方厘米)综合练习13.计算下面个图形的面积。(单位:厘米) (20+60)×20÷2
=80×20÷2
=800(平方厘米) 65×50+50×20÷2
=3250+500
=3750(平方厘米)综合练习15.CBC综合练习14.哪种说法正确?(单位:分米)√回顾反思
