力与平衡 单元测试2

本章知识结构
本章测试
1.在图5-1中，要将力F沿两条虚线分解成两个力，则A、B、C、D四个图中，可以分解的是（　　）
图5-1
思路解析：我们在分解力的时候两个分力应作为平行四边形的两个邻边，合力应作为平行四边形的对角线，所以，应选Ａ。
答案：A
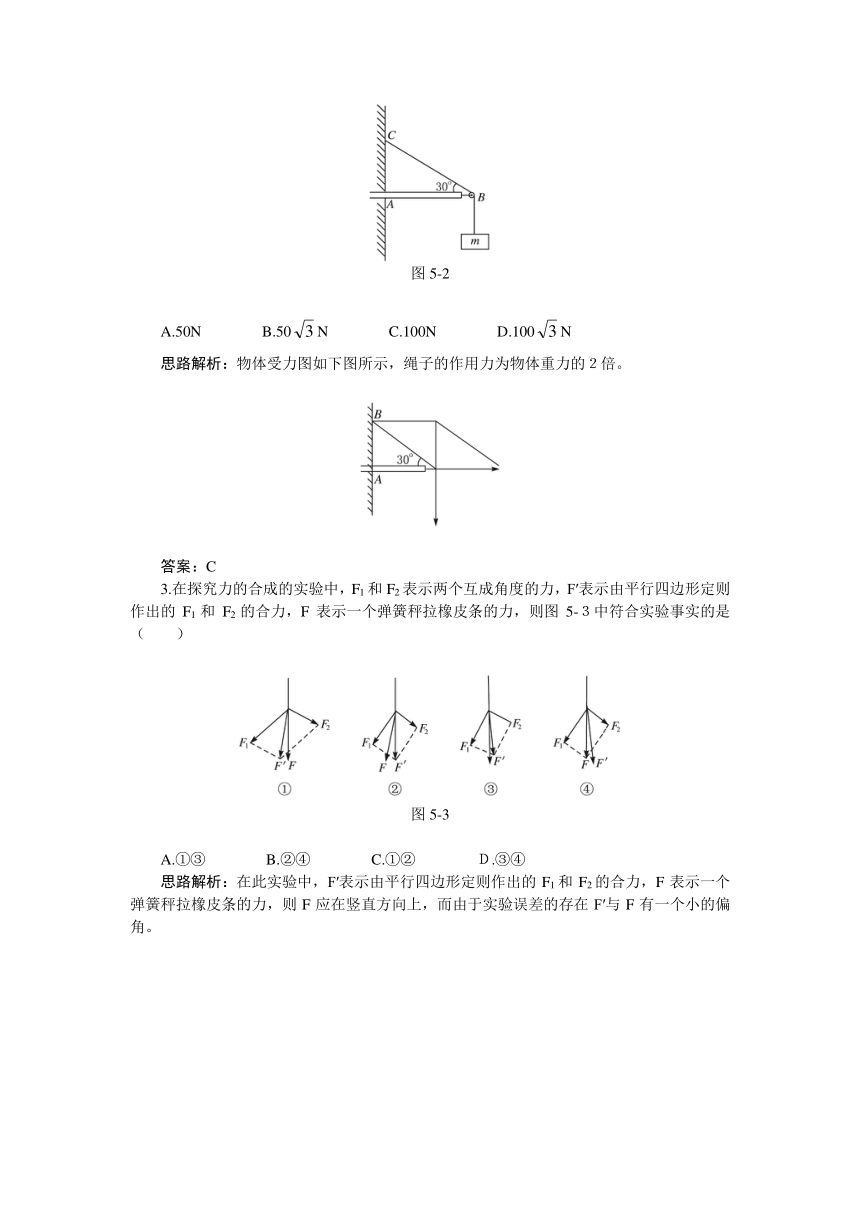
2.水平横梁的一端A插在墙壁内，另一端装有一小滑轮B。一轻绳的一端C固定于墙壁上，另一端跨过滑轮后悬挂一质量m=10kg的重物，∠CBA=30°，如图5-2所示，则滑轮受到绳子的作用力为（g取10m/s2）（　　）
图5-2
A.50N　　　　B.50N　　　　C.100N　　　　D.100N
思路解析：物体受力图如下图所示，绳子的作用力为物体重力的２倍。
答案：C
3.在探究力的合成的实验中，F1和F2表示两个互成角度的力，F′表示由平行四边形定则作出的F1和F2的合力，F表示一个弹簧秤拉橡皮条的力，则图5-３中符合实验事实的是（　　）
图5-3
A.①③　　　　B.②④　　　　C.①②　　　　Ｄ.③④
思路解析：在此实验中，F′表示由平行四边形定则作出的F1和F2的合力，F表示一个弹簧秤拉橡皮条的力，则F应在竖直方向上，而由于实验误差的存在F′与F有一个小的偏角。
答案：A
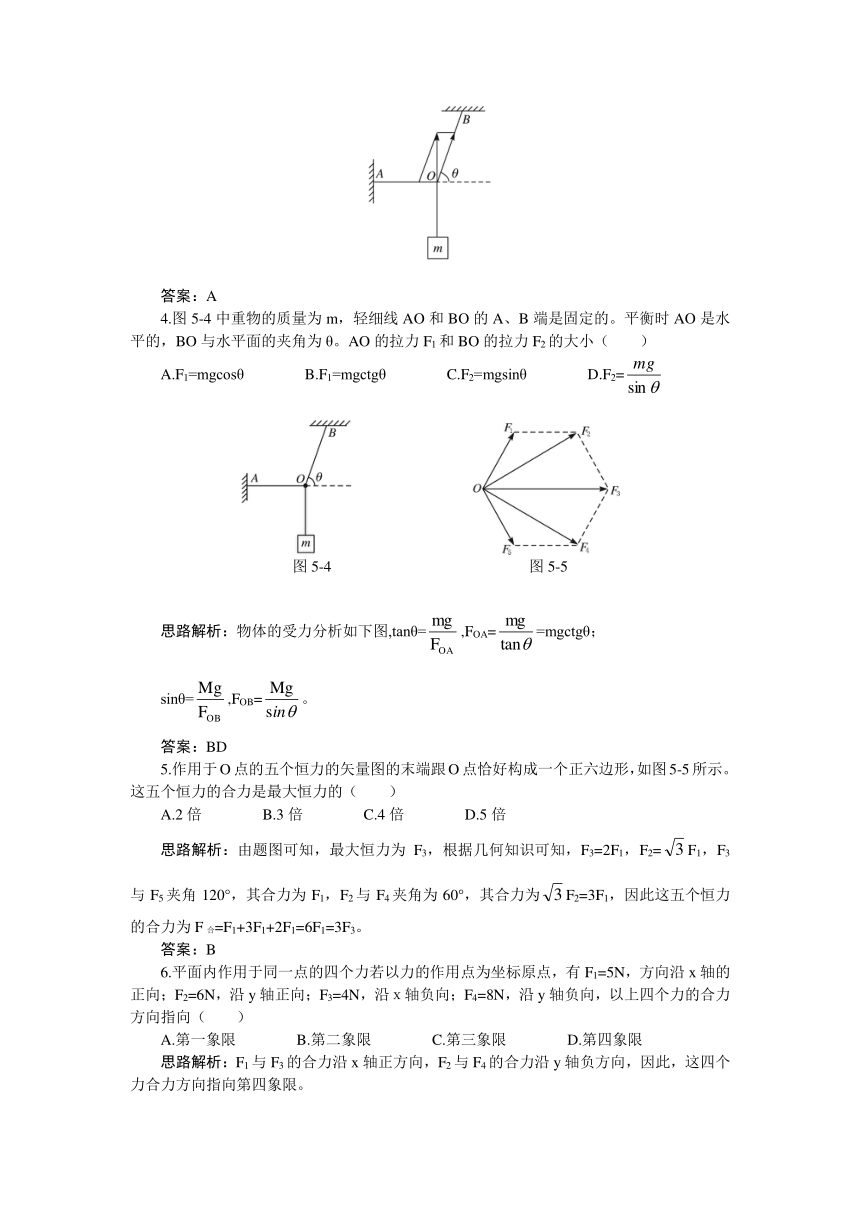
4.图5-4中重物的质量为m，轻细线AO和BO的A、B端是固定的。平衡时AO是水平的，BO与水平面的夹角为θ。AO的拉力F1和BO的拉力F2的大小（　　）
A.F1=mgcosθ　　　　B.F1=mgctgθ　　　　C.F2=mgsinθ　　　　D.F2=
　　　　　　　　
图5-4　　　　　　　　　　　　　图5-5
思路解析：物体的受力分析如下图,tanθ=,FOA==mgctgθ；
sinθ=,FOB=。
答案：BD
5.作用于O点的五个恒力的矢量图的末端跟O点恰好构成一个正六边形，如图5-5所示。这五个恒力的合力是最大恒力的（　　）
A.2倍　　　　B.3倍　　　　C.4倍　　　　D.5倍
思路解析：由题图可知，最大恒力为F3，根据几何知识可知，F3=2F1，F2=F1，F3与F5夹角120°，其合力为F1，F2与F4夹角为60°，其合力为F2=3F1，因此这五个恒力的合力为F合=F1+3F1+2F1=6F1=3F3。
答案：B
6.平面内作用于同一点的四个力若以力的作用点为坐标原点，有F1=5N，方向沿x轴的正向；F2=6N，沿y轴正向；F3=4N，沿ｘ轴负向；F4=8N，沿y轴负向，以上四个力的合力方向指向（　　）
A.第一象限　　　　B.第二象限　　　　C.第三象限　　　　D.第四象限
思路解析：F1与F3的合力沿x轴正方向，F2与F4的合力沿y轴负方向，因此，这四个力合力方向指向第四象限。
答案：D
7.同一平面内的三个力，大小分别为4N、6N、7N，若三力同时作用于某一物体，则该物体所受三力合力的最大值和最小值分别为（　　）
A.17N、3N　　　　B.17N、0　　　　C.9N、0　　　　D.5N、3N
思路解析：当三个力在同一直线上方向相同时，三个力的合力最大为17N，4N、6N这两个力的合力的范围是2～10N，第三个力7N介于这个范围内，若满足方向相反，则三个力的合力最小为零。
答案：B
8.如图5-6所示，一个重为5N的大砝码，用细线悬挂在O点，现在用力F拉砝码，使悬线偏离竖直方向30°时处于静止状态，此时所用拉力F的最小值为（　　）
A.5.0N　　　　B.2.5N　　　　C.8.65N　　　　D.4.3N
　　　　　　　　　
图5-6　　　　　　　　　　　　　图5-7
思路解析：两悬线拉力的合力大小等于重力，方向竖直向上，这满足“已知合力的大小和方向，已知一个分力的方向，判断第二个分力的最小值”这种情况，当两分力垂直时，第二个分力有最小值，所以F=Gsin30°=5×N=2.5N。
答案：B
9.如图5-7所示，用绳索将重球挂在墙上，不考虑墙的摩擦。如果把绳的长度增加一些，则球对绳的拉力F1和球对墙的压力F2的变化情况是（　　）
A.F1增大，F2减小　　　　B.F1减小，F2增大
C.F1和F2都减小　　　　 D.F1和F2都增大
思路解析：采用图解法。F1和F2的合力与重力大小相等，方向相反，当绳长增加时，绳与墙的夹角变小，力的变化如下图所示，由分析可得，F1和F2都减小。
答案：C
10.物体静止在斜面上，若斜面倾角增大（物体仍静止），物体受到的斜面的支持力和摩擦力的变化情况是（　　）
A.支持力增大，摩擦力增大
B.支持力增大，摩擦力减小
C.支持力减小，摩擦力增大
D.支持力减小，摩擦力减小
思路解析：对重力正交分解得，支持力FN=mgcosθ，静摩擦力Ff=mgsinθ，可知当斜面倾角增大时，支持力减小，摩擦力增大。
答案：C
11.一根长2m，重为G的不均匀直棒AB，用两根细绳水平悬挂在天花板上，如图5-8所示，求直棒重心C的位置应在距B端＿＿＿＿处。
　　　
图5-8　　　　　　　　图5-9
思路解析：当一个物体受三个力作用而处于平衡状态，如果其中两个力的作用线相交于一点。则第三个力的作用线必通过前两个力作用线的相交点，把O1A和O2B延长相交于O点，则重心C一定在过O点的竖直线上，如题图所示由几何知识可知：
BO=AB/2=1m　BC=BO/2=0.5m
答案：0.5m
12.作用于同一点的两个力F1、F2的合力F随F1、F2的夹角变化的情况如图5-9所示，则F1=＿＿＿＿，F2=＿＿＿＿。
思路解析：当两力夹角为90°时，合力F=，当两力夹角为180°时，两力合力为F′=F1-F2，代入数据得F1=40N，F2=30N。
答案：40N　30N
13同一平面中的三个力大小分别为F1=6N、F2=7N、F3=8N，这三个力沿不同方向作用于同一物体，该物体做匀速运动。若撤销F3，这时物体所受F1、F2的合力大小等于N，合力的方向。
思路解析：F1、F2的合力大小应与F3大小相等，为8N，方向与F3的方向相反。
答案：8　与F3方向相反
14用两根钢丝绳AB、BC将一根电线杆OB垂直固定在地面上，且它们在同一个平面内，如图5-10所示，设AO=5m，OC=9m，OB=12m，为使电线杆不发生倾斜，两根绳上的张力之比为。
图5-10
思路解析：为使电线杆不发生倾斜，两根绳上的张力沿水平方向的分力大小相等。由几何知识可得AB=13m，BC=15m。设AB与竖直方向夹角为α，BC与竖直方向夹角为β，则有FABsinα=FBCsinβ，所以=，代入数据得=。
答案：39∶25
15.如图5-11所示，一轻质三角形框架B处悬挂一定滑轮（质量可忽略不计）。一体重为500N的人通过跨定滑轮的轻绳匀速提起一重为300N的物体。
图5-11
（1）此时人对地面的压力是多大？
（2）斜杆BC，横杆AB所受的力是多大？
解：（1）先以人为研究对象，人受三个力作用，重力G、地面对人的支持力FN、绳子的拉力FT。由平衡方程可得：FN+FT=G，解得FN=200N。即人对地面的压力为200N。
（2）以B点为研究对象，其受力情况如下图所示。将绳子的拉力F分解为两个力：一个分力是对AB杆的拉力、一个分力是对BC杆的压力。F=2G=600N，由题意及受力分解图可知：
FAB=Ftan30°=200N
FBC==4003N。