2018-2019学年度冀教版九年级数学上册《第25章图形的相似》单元检测试卷(有答案)
文档属性
| 名称 | 2018-2019学年度冀教版九年级数学上册《第25章图形的相似》单元检测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 116.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-22 18:46:12 | ||
图片预览


文档简介
2018-2019学年度第一学期冀教版九年级数学上册_
第25章_ 图形的相似 _单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知
??
??
=
5
13
,则
??+??
?????
的值是( )
A.
2
3
B.
3
2
C.
9
4
D.
4
9
?2.两个相似三角形对应边之比是1:5,那么它们的周长比是( )
A.1:
5
B.1:25
C.1:5
D.
5
:1
?3.在比例尺为1:500的地图上,量得甲,乙两地的距离为2.5????,则甲、乙两地的实际距离是( )
A.1250米
B.12.5米
C.125米
D.1.25米
?4.如图,添加下列一个条件,不能使△??????∽△??????的是( )
/
A.
????
????
=
????
????
B.∠??????=∠??
C.
????
????
=
????
????
D.∠??????=∠??
?5.如图,??是线段????的黄金分割点(????>????),四边形????????、四边形????????都是正方形,且面积分别为
??
1
、
??
2
,四边形????????、四边形????????都是矩形,且面积分别为
??
3
、
??
4
,下列说法正确的是( )
/
A.
??
2
=
5
?1
2
??
1
B.
??
2
=
??
3
C.
??
3
=
5
?1
2
??
4
D.
??
4
=
5
?1
2
?6.如图所示,在△??????中,?????//??????//?????,且????到????、????的距离之比为1:2.若△??????的面积为32,△??????的面积为2,则△??????的面积??等于( )
/
A.6
B.8
C.10
D.12
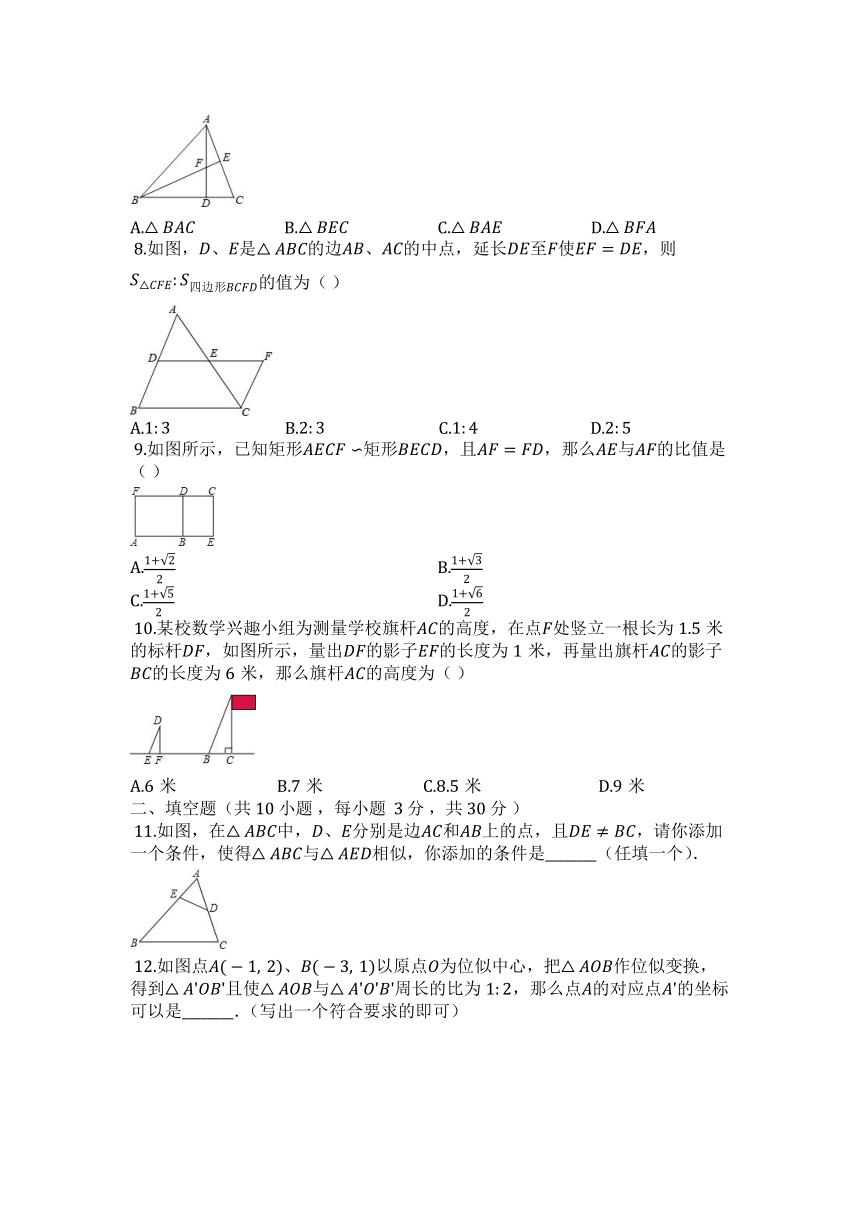
?7.如图:已知??是△??????中的边????上的一点,∠??????=∠??,∠??????的平分线交边????于??,交????于??,那么下列三角形中与△??????一定相似的是( )
/
A.△??????
B.△??????
C.△??????
D.△??????
?8.如图,??、??是△??????的边????、????的中点,延长????至??使????=????,则
??
△??????
:
??
四边形????????
的值为( )
/
A.1:3
B.2:3
C.1:4
D.2:5
?9.如图所示,已知矩形????????∽矩形????????,且????=????,那么????与????的比值是( )
/
A.
1+
2
2
B.
1+
3
2
C.
1+
5
2
D.
1+
6
2
?10.某校数学兴趣小组为测量学校旗杆????的高度,在点??处竖立一根长为1.5米的标杆????,如图所示,量出????的影子????的长度为1米,再量出旗杆????的影子????的长度为6米,那么旗杆????的高度为( )
/
A.6米
B.7米
C.8.5米
D.9米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,在△??????中,??、??分别是边????和????上的点,且????≠????,请你添加一个条件,使得△??????与△??????相似,你添加的条件是________(任填一个).
/
?12.如图点??(?1,?2)、??(?3,?1)以原点??为位似中心,把△??????作位似变换,得到△??′????′且使△??????与△??′??′??′周长的比为1:2,那么点??的对应点??′的坐标可以是________.(写出一个符合要求的即可)
/
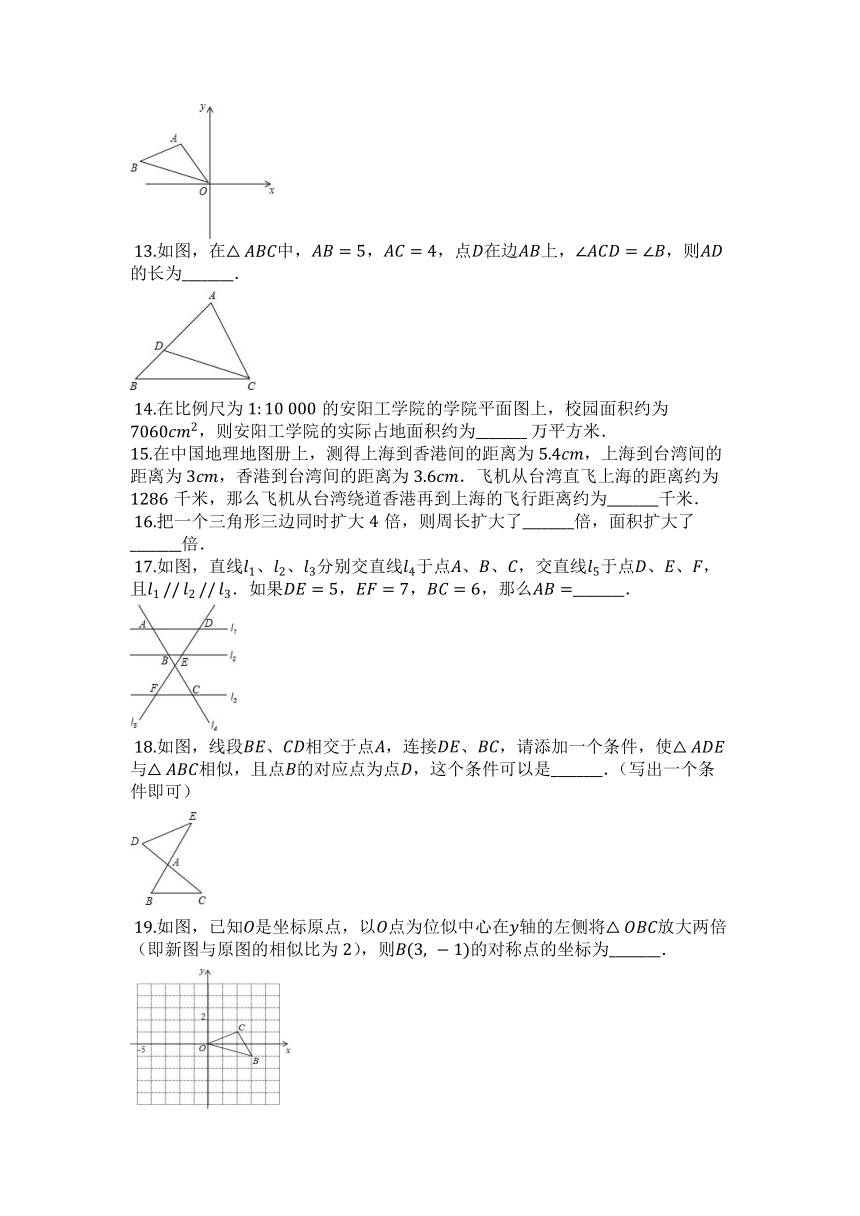
?13.如图,在△??????中,????=5,????=4,点??在边????上,∠??????=∠??,则????的长为________.
/
?14.在比例尺为1:10?000的安阳工学院的学院平面图上,校园面积约为7060??
??
2
,则安阳工学院的实际占地面积约为________?万平方米.?
15.在中国地理地图册上,测得上海到香港间的距离为5.4????,上海到台湾间的距离为3????,香港到台湾间的距离为3.6????.飞机从台湾直飞上海的距离约为1286千米,那么飞机从台湾绕道香港再到上海的飞行距离约为________千米.
?16.把一个三角形三边同时扩大4倍,则周长扩大了________倍,面积扩大了________倍.
?17.如图,直线
??
1
、
??
2
、
??
3
分别交直线
??
4
于点??、??、??,交直线
??
5
于点??、??、??,且
??
1
?//?
??
2
?//?
??
3
.如果????=5,????=7,????=6,那么????=________.
/
?18.如图,线段????、????相交于点??,连接????、????,请添加一个条件,使△??????与△??????相似,且点??的对应点为点??,这个条件可以是________.(写出一个条件即可)
/
?19.如图,已知??是坐标原点,以??点为位似中心在??轴的左侧将△??????放大两倍(即新图与原图的相似比为2),则??(3,??1)的对称点的坐标为________.
/
?20.如图,△??????中,????是角平分线,过??作?????//?????交????于点??,????=5????,????=3????,则????的长为________????.
/
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,在△??????中,????=15,????=12,????=5,过点??作直线????与????交于点??,使截得的三角形与△??????相似,求????的长.
/
?
22.如图,点??为△??????的边????上的一点,连结????,若∠1=∠??.
/
(1)求证:△??????∽△??????;?
(2)若????=4,????=5,求????的长.
?
23.正方形????????中,点??、??分别在????和????上,且????⊥????,
/
(1)求证:△??????∽△??????;
(2)△??????和△??????相似吗?若相似,请给出证明,若不相似,请举一个反例说明.
?
24.已知:如图,点??、??、??分别在△??????的边????、????、????上,?????//?????,????=2????,????=2????.
/
(1)求证:?????//?????;
(2)联结????,当∠??????=∠??时,求证:????=
2
????.
?
25.如图,在梯形????????中,?????//?????,点??是边????的中点,连接????,交????于点??,????的延长线交????的延长线于点??.
/
(1)求证:
????
????
=
????
????
;
(2)若????=2,????=5,求线段????的长;
(3)找出图中所有的位似三角形.
?
26.(1)如图一:小明想测量一棵树的高度????,在阳光下,小明测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长????为1.5米,落在地面上的影长????为3米,则树高????为多少米.26.
(2)如图二:在阳光下,小明在某一时刻测得与地面垂直、长为1??的杆子在地面上的影子长为2??,在斜坡上影长为1.5??,他想测量电线杆????的高度,但其影子恰好落在土坡的坡面????和地面????上,量得????=3??,????=10??,求电线杆的高度.
/
答案
1.C
2.C
3.B
4.A
5.B
6.B
7.C
8.C
9.C
10.D
11.∠??????=∠??????(∠??????=∠??????或
????
????
=
????
????
或
????
????
=
????
????
或?????//?????)
12.(?2,?4)或(2,??4)
13.
16
5
14.7060
15.3858
16.416
17.
30
7
18.∠??=∠??
19.(?6,?2)
20.4.5
21.解:如图所示:过点??作????⊥????于点??, ∵????⊥????,∠??=
90
°
, ∴?????//?????, ∴△??????∽△??????, ∴
????
????
=
????
????
, ∴
5
15
=
????
12
, 解得:????=4; 当??′??⊥????于点??, ∵∠??=∠??′????,∠??=∠??, ∴△??????∽△??′????, ∴
????
????
=
????′
????
, ∵????=15,????=12,∠??=
90
°
, ∴????=9, ∴
5
9
=
????′
12
, 解得:????′=
20
3
, 故使截得的三角形与△??????相似,则????的长为4或
20
3
.
/
22.(1)证明:∵∠1=∠??,∠??=∠??, ∴△??????∽△??????;(2)∵????=4,????=5, ∴????=9, ∵△??????∽△??????, ∴
????
????
=
????
????
, 即:
????
9
=
4
????
, ∴????=6.
23.证明:(1)∵正方形????????中,点??、??分别在????和????上,且????⊥????, ∴∠??????+∠??????=
90
°
,∠??????+∠??????=
90
°
,∠??=∠??=
90
°
, ∴∠??????=∠??????, ∴△??????∽△??????;
/
(2)不相似,连接????,先假设△??????∽△??????, ∵四边形????????是正方形, ∴∠??????=∠??????=
90
°
, 又∵????⊥????, ∴∠??????=
90
°
, 又∵△??????∽△??????, ∴△??????中必有一个直角, 又∵∠??????、∠??????、∠??????<
90
°
, ∴假设错误,△??????和△??????不相似.
24.证明:(1)∵????=2????,????=2????, ∴
????
????
=
????
????
, 又∵?????//?????,
/
∴
????
????
=
????
????
, ∴
????
????
=
????
????
., ∴?????//?????;(2)∵∠??????=∠??,∠??=∠??, ∴△??????∽△??????, ∴
????
????
=
????
????
, 又∵????=2????,????=2????, ∴????=
2
3
????,????=
1
3
????, ∴
????
????
=
2????
????
, ∴??
??
2
=2??
??
2
, 即????=
2
????.
25.证明:(1)∵?????//?????, ∴∠??????=∠??????, ∵∠??=∠??, ∴△??????∽△??????, ∴
????
????
=
????
????
, ∵????=????, ∴
????
????
=
????
????
;(2)∵?????//?????, ∴△??????∽△??????, ∴
/
????
????
=
????
????
, 由(1)知
????
????
=
????
????
, ∴
????
????
=
????
????
, 设????=??, ∵????=2,????=5, ∴
2
5
=
??
??+5
, 解得:??=
10
3
, ∴????=
10
3
;(3)图中的位似三角形有:△??????与△??????,△??????与△??????.
26.树高为5.25米.(2)作????⊥????于??.
/
????对应的旗杆的高度:根据同一时刻物高与影长成比例,得10÷2=5; ????对应的旗杆的高度:3÷1.5=2; 故旗杆的高度是5+2=7??.
第25章_ 图形的相似 _单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知
??
??
=
5
13
,则
??+??
?????
的值是( )
A.
2
3
B.
3
2
C.
9
4
D.
4
9
?2.两个相似三角形对应边之比是1:5,那么它们的周长比是( )
A.1:
5
B.1:25
C.1:5
D.
5
:1
?3.在比例尺为1:500的地图上,量得甲,乙两地的距离为2.5????,则甲、乙两地的实际距离是( )
A.1250米
B.12.5米
C.125米
D.1.25米
?4.如图,添加下列一个条件,不能使△??????∽△??????的是( )
/
A.
????
????
=
????
????
B.∠??????=∠??
C.
????
????
=
????
????
D.∠??????=∠??
?5.如图,??是线段????的黄金分割点(????>????),四边形????????、四边形????????都是正方形,且面积分别为
??
1
、
??
2
,四边形????????、四边形????????都是矩形,且面积分别为
??
3
、
??
4
,下列说法正确的是( )
/
A.
??
2
=
5
?1
2
??
1
B.
??
2
=
??
3
C.
??
3
=
5
?1
2
??
4
D.
??
4
=
5
?1
2
?6.如图所示,在△??????中,?????//??????//?????,且????到????、????的距离之比为1:2.若△??????的面积为32,△??????的面积为2,则△??????的面积??等于( )
/
A.6
B.8
C.10
D.12
?7.如图:已知??是△??????中的边????上的一点,∠??????=∠??,∠??????的平分线交边????于??,交????于??,那么下列三角形中与△??????一定相似的是( )
/
A.△??????
B.△??????
C.△??????
D.△??????
?8.如图,??、??是△??????的边????、????的中点,延长????至??使????=????,则
??
△??????
:
??
四边形????????
的值为( )
/
A.1:3
B.2:3
C.1:4
D.2:5
?9.如图所示,已知矩形????????∽矩形????????,且????=????,那么????与????的比值是( )
/
A.
1+
2
2
B.
1+
3
2
C.
1+
5
2
D.
1+
6
2
?10.某校数学兴趣小组为测量学校旗杆????的高度,在点??处竖立一根长为1.5米的标杆????,如图所示,量出????的影子????的长度为1米,再量出旗杆????的影子????的长度为6米,那么旗杆????的高度为( )
/
A.6米
B.7米
C.8.5米
D.9米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,在△??????中,??、??分别是边????和????上的点,且????≠????,请你添加一个条件,使得△??????与△??????相似,你添加的条件是________(任填一个).
/
?12.如图点??(?1,?2)、??(?3,?1)以原点??为位似中心,把△??????作位似变换,得到△??′????′且使△??????与△??′??′??′周长的比为1:2,那么点??的对应点??′的坐标可以是________.(写出一个符合要求的即可)
/
?13.如图,在△??????中,????=5,????=4,点??在边????上,∠??????=∠??,则????的长为________.
/
?14.在比例尺为1:10?000的安阳工学院的学院平面图上,校园面积约为7060??
??
2
,则安阳工学院的实际占地面积约为________?万平方米.?
15.在中国地理地图册上,测得上海到香港间的距离为5.4????,上海到台湾间的距离为3????,香港到台湾间的距离为3.6????.飞机从台湾直飞上海的距离约为1286千米,那么飞机从台湾绕道香港再到上海的飞行距离约为________千米.
?16.把一个三角形三边同时扩大4倍,则周长扩大了________倍,面积扩大了________倍.
?17.如图,直线
??
1
、
??
2
、
??
3
分别交直线
??
4
于点??、??、??,交直线
??
5
于点??、??、??,且
??
1
?//?
??
2
?//?
??
3
.如果????=5,????=7,????=6,那么????=________.
/
?18.如图,线段????、????相交于点??,连接????、????,请添加一个条件,使△??????与△??????相似,且点??的对应点为点??,这个条件可以是________.(写出一个条件即可)
/
?19.如图,已知??是坐标原点,以??点为位似中心在??轴的左侧将△??????放大两倍(即新图与原图的相似比为2),则??(3,??1)的对称点的坐标为________.
/
?20.如图,△??????中,????是角平分线,过??作?????//?????交????于点??,????=5????,????=3????,则????的长为________????.
/
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,在△??????中,????=15,????=12,????=5,过点??作直线????与????交于点??,使截得的三角形与△??????相似,求????的长.
/
?
22.如图,点??为△??????的边????上的一点,连结????,若∠1=∠??.
/
(1)求证:△??????∽△??????;?
(2)若????=4,????=5,求????的长.
?
23.正方形????????中,点??、??分别在????和????上,且????⊥????,
/
(1)求证:△??????∽△??????;
(2)△??????和△??????相似吗?若相似,请给出证明,若不相似,请举一个反例说明.
?
24.已知:如图,点??、??、??分别在△??????的边????、????、????上,?????//?????,????=2????,????=2????.
/
(1)求证:?????//?????;
(2)联结????,当∠??????=∠??时,求证:????=
2
????.
?
25.如图,在梯形????????中,?????//?????,点??是边????的中点,连接????,交????于点??,????的延长线交????的延长线于点??.
/
(1)求证:
????
????
=
????
????
;
(2)若????=2,????=5,求线段????的长;
(3)找出图中所有的位似三角形.
?
26.(1)如图一:小明想测量一棵树的高度????,在阳光下,小明测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长????为1.5米,落在地面上的影长????为3米,则树高????为多少米.26.
(2)如图二:在阳光下,小明在某一时刻测得与地面垂直、长为1??的杆子在地面上的影子长为2??,在斜坡上影长为1.5??,他想测量电线杆????的高度,但其影子恰好落在土坡的坡面????和地面????上,量得????=3??,????=10??,求电线杆的高度.
/
答案
1.C
2.C
3.B
4.A
5.B
6.B
7.C
8.C
9.C
10.D
11.∠??????=∠??????(∠??????=∠??????或
????
????
=
????
????
或
????
????
=
????
????
或?????//?????)
12.(?2,?4)或(2,??4)
13.
16
5
14.7060
15.3858
16.416
17.
30
7
18.∠??=∠??
19.(?6,?2)
20.4.5
21.解:如图所示:过点??作????⊥????于点??, ∵????⊥????,∠??=
90
°
, ∴?????//?????, ∴△??????∽△??????, ∴
????
????
=
????
????
, ∴
5
15
=
????
12
, 解得:????=4; 当??′??⊥????于点??, ∵∠??=∠??′????,∠??=∠??, ∴△??????∽△??′????, ∴
????
????
=
????′
????
, ∵????=15,????=12,∠??=
90
°
, ∴????=9, ∴
5
9
=
????′
12
, 解得:????′=
20
3
, 故使截得的三角形与△??????相似,则????的长为4或
20
3
.
/
22.(1)证明:∵∠1=∠??,∠??=∠??, ∴△??????∽△??????;(2)∵????=4,????=5, ∴????=9, ∵△??????∽△??????, ∴
????
????
=
????
????
, 即:
????
9
=
4
????
, ∴????=6.
23.证明:(1)∵正方形????????中,点??、??分别在????和????上,且????⊥????, ∴∠??????+∠??????=
90
°
,∠??????+∠??????=
90
°
,∠??=∠??=
90
°
, ∴∠??????=∠??????, ∴△??????∽△??????;
/
(2)不相似,连接????,先假设△??????∽△??????, ∵四边形????????是正方形, ∴∠??????=∠??????=
90
°
, 又∵????⊥????, ∴∠??????=
90
°
, 又∵△??????∽△??????, ∴△??????中必有一个直角, 又∵∠??????、∠??????、∠??????<
90
°
, ∴假设错误,△??????和△??????不相似.
24.证明:(1)∵????=2????,????=2????, ∴
????
????
=
????
????
, 又∵?????//?????,
/
∴
????
????
=
????
????
, ∴
????
????
=
????
????
., ∴?????//?????;(2)∵∠??????=∠??,∠??=∠??, ∴△??????∽△??????, ∴
????
????
=
????
????
, 又∵????=2????,????=2????, ∴????=
2
3
????,????=
1
3
????, ∴
????
????
=
2????
????
, ∴??
??
2
=2??
??
2
, 即????=
2
????.
25.证明:(1)∵?????//?????, ∴∠??????=∠??????, ∵∠??=∠??, ∴△??????∽△??????, ∴
????
????
=
????
????
, ∵????=????, ∴
????
????
=
????
????
;(2)∵?????//?????, ∴△??????∽△??????, ∴
/
????
????
=
????
????
, 由(1)知
????
????
=
????
????
, ∴
????
????
=
????
????
, 设????=??, ∵????=2,????=5, ∴
2
5
=
??
??+5
, 解得:??=
10
3
, ∴????=
10
3
;(3)图中的位似三角形有:△??????与△??????,△??????与△??????.
26.树高为5.25米.(2)作????⊥????于??.
/
????对应的旗杆的高度:根据同一时刻物高与影长成比例,得10÷2=5; ????对应的旗杆的高度:3÷1.5=2; 故旗杆的高度是5+2=7??.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
