华师大版九年级数学下册《第27章圆》单元检测试题(有答案)
文档属性
| 名称 | 华师大版九年级数学下册《第27章圆》单元检测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-22 19:44:56 | ||
图片预览



文档简介
2017-2018学年度第二学期华师大版九年级数学下册
第27章 圆 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,⊙??是△??????的内切圆,点??、??分别为边????、????上的点,且????为⊙??的切线,若△??????的周长为25,????的长是9,则△??????的周长是( )
/
A.7
B.8
C.9
D.16
?2.如图,已知????是⊙??的直径,点??、??在⊙??上,
????
=
????
,∠??????=
60
°
,则∠??????的度数是( )
/
A.
20
°
B.
25
°
C.
30
°
D.
40
°
?3.如图,在⊙??中,????是直径,点??是
????
的中点,点??是
????
的中点,则∠??????的度数( )
/
A.
30
°
B.
25
°
C.
22.5
°
D.不能确定
?4.如图,王大伯家屋后有一块长12??、宽8??的长方形空地,他在以较长边????为直径的半圆内种菜,他家养的一只羊平时拴在??处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
/
A.3??
B.4??
C.5??
D.6??
?5.一根水平放置的圆柱形输水管道的横截面如图所示,其中有水部分水面宽0.4米,最深处水深0.1米,则此输水管道的直径等于( )
/
A.0.2米
B.0.25米
C.0.4米
D.0.5米
?6.已知:如图,△??????中,∠??=
60
°
,????为定长,以????为直径的⊙??分别交????、????于点??、??.连接????、????.下列结论:①????=2????;②??点到????的距离不变;③????+????=2????;④????为外接圆的切线.其中正确的结论是( )
/
A.①②
B.③④
C.①②③
D.①②④
?7.如图,在⊙0中,??为弧??????的中点,????⊥????交⊙0于??,若????=????=1,????的长为( )
/
A.2.5
B.3
C.3.5
D.4
?8.在直角坐标系中,以原点为圆心,4为半径作圆,该圆上到直线??=???+
2
的距离等于2的点共有( )
A.1个
B.2个
C.3个
D.4个
?9.如图,⊙??的半径为1,????是⊙??的一条弦,且????=
3
,则弦????所对圆周角的度数为( )
/
A.
30
°
B.
60
°
C.
30
°
或
150
°
D.
60
°
或
120
°
?10.如图,△??????的????边与⊙??相切于??点,若直径????=????=4,则????的值是( )
/
A.2
2
B.2
3
C.4
2
D.4
3
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,△??????中,∠??=
25
°
,∠??=
85
°
,过点??、??的圆交边????、????分别于点??、??,则∠??????=________
°
.
/ / /
?12.⊙
??
1
与⊙
??
2
相交于??、??,若
??
1
??
2
=7????,????=6????,⊙
??
1
的半径为5????,则⊙
??
2
的半径为________.
?13.已知:如图,三角形??????内接于⊙??,????为直径,过点??作直线????,要使得????是⊙??的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
?14.如图,????为⊙??的弦,直径????为4,????⊥????于??,∠??=
30
°
,则
????
的长为________(结果保留??).
?15.如图,以△??????的直角边????为直径的半圆??与斜边????交于点??,??是????边的中点.若????、????的长是方程
??
2
?6??+8=0的两个根,则图中阴影部分的面积为________.
/ / /
?16.如图,??是半径为2的⊙??外一点,????=4,????是⊙??的切线,点??是切点,弦?????//?????,连接????,则图中阴影部分的面积为________.
?17.如图,从半径为10????的圆形纸片上剪去
1
5
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
18.一个直角三角形的两条边长是方程
??
2
?7??+12=0的两个根,则此直角三角形的外接圆的面积为________.
?19.如图,将半径为1、圆心角为
60
°
的扇形纸片??????,在直线??上向右作无滑动的滚动至扇形
??
′
??
′
??
′
处,则顶点??经过的路线总长为________.
/ /
?20.已知△??????的内切圆半径为??,∠??=
60
°
,????=2
3
,则??的取值范围是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
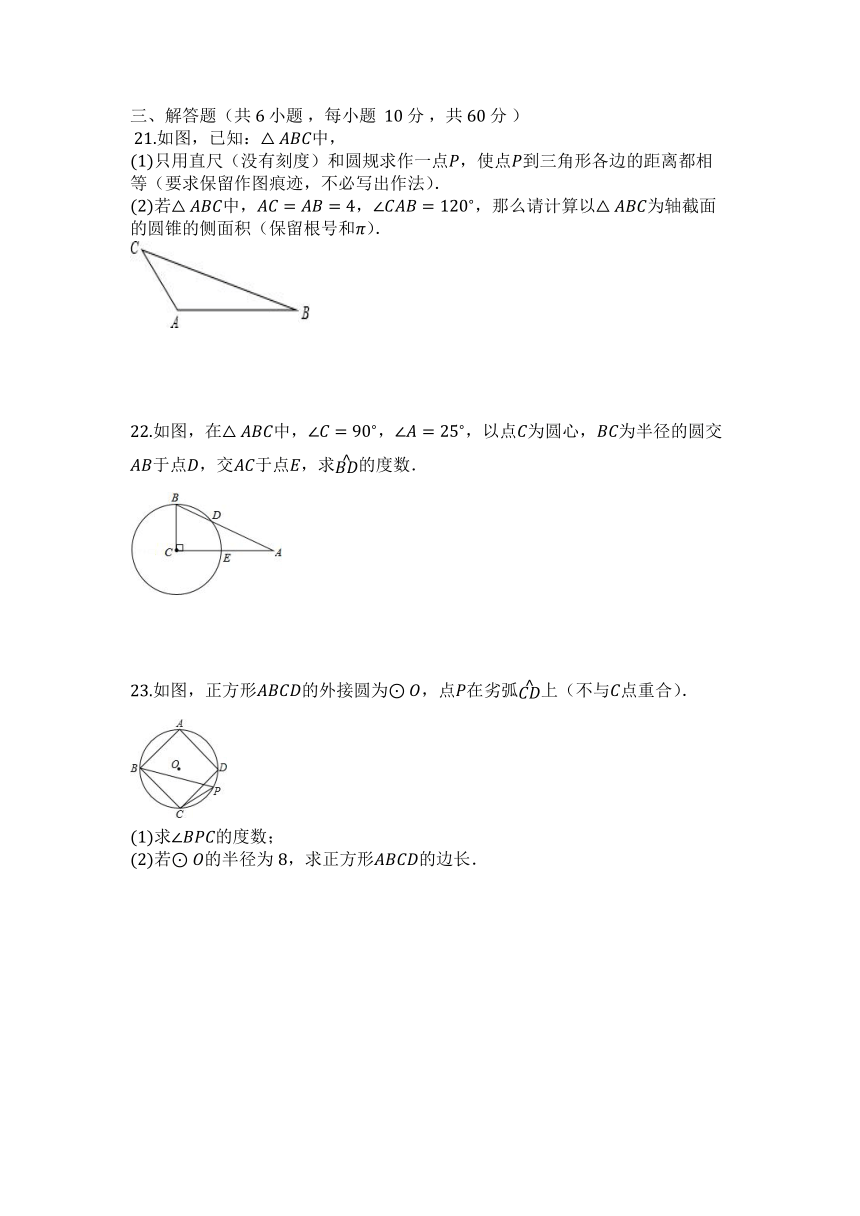
?21.如图,已知:△??????中,
(1)只用直尺(没有刻度)和圆规求作一点??,使点??到三角形各边的距离都相等(要求保留作图痕迹,不必写出作法).
(2)若△??????中,????=????=4,∠??????=
120
°
,那么请计算以△??????为轴截面的圆锥的侧面积(保留根号和??).
/
?
22.如图,在△??????中,∠??=
90
°
,∠??=
25
°
,以点??为圆心,????为半径的圆交????于点??,交????于点??,求
????
的度数.
/
?
23.如图,正方形????????的外接圆为⊙??,点??在劣弧
????
上(不与??点重合).
/
(1)求∠??????的度数;
(2)若⊙??的半径为8,求正方形????????的边长.
?
24.如图,以????为直径的⊙??经过????的中点??,????⊥????于点??.
/
(1)求证:????是⊙??的切线;
(2)当????=1,∠??=
30
°
时,求图中阴影部分的面积.
?
25.已知:??是⊙??外的一点,????=4,????交⊙??于点??,且??是????的中点,??是⊙??上任意一点.
/
(1)如图1,若????是⊙??的切线,求∠??????的大小;
(2)如图2,若∠??????=
90
°
,求????被⊙??截得的弦????的长.
?
26.????是⊙??的直径,????是⊙??的弦,过??作⊙??的切线,交????的延长线于??.作弦????,使∠??????=∠??????,连接????.
/
(1)求证:????是⊙??的切线;
(2)当∠??????=________
°
时,????⊥????,证明你的结论;
(3)????与????相交于??,当????=2,????=3时,求??到⊙??的切线长.
答案
1.A
2.C
3.C
4.B
5.D
6.A
7.B
8.D
9.D
10.C
11.70
12.
130
????或3
2
????
13.????⊥????∠??????=∠??∠??????+∠??????=
90
°
14.
2
3
??
15.4
3
?
4
3
??
16.
2
3
??
17.6????
18.4??或6.25??
19.
4
3
??
20.021.解:(1)作任意两角的角平分线,其交点即为所求作的点??.
/
(2)过??作????⊥????于??
/
∵????=????=4,∠??????=
120
°
∴由三角函数可得:????=2
3
∴??=4,??=2
3
∴??=??????=8
3
??.
22.解:连结????,如图,
/
∵∠??=
90
°
,∠??=
25
°
, ∴∠??=
90
°
?
25
°
=
65
°
, ∵????=????, ∴∠??=∠??????=
65
°
, ∴∠??????=
180
°
?
65
°
?
65
°
=
50
°
, ∴
????
的度数为
50
°
.
23.解:(1)连接????,????, ∵四边形????????为正方形, ∴∠??????=
90
°
, ∴∠??=
1
2
∠??????=
45
°
;
/
(2)过点??作????⊥????于点??, ∵????=????,∠??????=
90
°
, ∴∠??????=
45
°
, ∴????=????, ∵??
??
2
+??
??
2
=??
??
2
, ∴????=
??
??
2
2
=
64
2
=4
2
∴????=2????=2×4
2
=8
2
.
24.解:(1)连接????, ∵????是⊙??的直径,??是????的中点, ∴????是△??????的中位线, ∴?????//?????, ∵????⊥????, ∴????⊥????, ∵点??在圆上, ∴????为⊙??的切线;????
/
(2)∵∠??=
30
°
,????=1,∠??????=
90
°
, ∴????=2, ∵?????//?????, ∴∠??????=
30
°
, ∵????=????, ∴∠??????=∠??????=
30
°
, ∴∠??????=
120
°
, ∴????=
2
3
3
, ∴阴影部分面积??=
120???×(
2
3
3
)
2
360
?
1
2
×2×
3
3
=
4??
9
?
3
3
.
25.解:(1)如图1,∵????是⊙??的切线, ∴????⊥????,
/
∵??是????的中点, ∴????=2????, 在????△??????中,cos∠??????=
????
????
=
1
2
, ∴∠??????=
60
°
;(2)作????⊥????于??,如图2,则????=????, ∵∠??????=
90
°
,????=4,????=2, ∴????=
2
2
+
4
2
=2
5
, ∵∠??????=∠??????, ∴????△??????∽????△??????, ∴????:????=????:????,即????:2=2:2
5
, ∴????=
2
5
5
, ∴????=2????=
4
5
5
.
26.证明:(1)连接????,????; ∵????是圆的切线, ∴∠??????=
90
°
. ∵∠??????=∠??????, ∴∠??????=∠??????. ∵????=????,????=????, ∴△???????△??????. ∴∠??????=∠??????=
90
°
. ∴????是⊙??的切线.
/
(2)
45
°
. ∵∠??????=
90
°
, ∴四边形????????为正方形. ∴????⊥????.(3)根据题意,得圆的半径是5,则????=7, ∵????=????,∠??????=∠??????, ∴????垂直平分????. ∵?????????=?????????=21,????=????=
21
, 设????=??,????=??, 则有
??
2
=21+(3+??
)
2
??
2
=??(??+10)
, 解得
??=
5
2
21
??=7.5
, 即????=
5
2
21
.
第27章 圆 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,⊙??是△??????的内切圆,点??、??分别为边????、????上的点,且????为⊙??的切线,若△??????的周长为25,????的长是9,则△??????的周长是( )
/
A.7
B.8
C.9
D.16
?2.如图,已知????是⊙??的直径,点??、??在⊙??上,
????
=
????
,∠??????=
60
°
,则∠??????的度数是( )
/
A.
20
°
B.
25
°
C.
30
°
D.
40
°
?3.如图,在⊙??中,????是直径,点??是
????
的中点,点??是
????
的中点,则∠??????的度数( )
/
A.
30
°
B.
25
°
C.
22.5
°
D.不能确定
?4.如图,王大伯家屋后有一块长12??、宽8??的长方形空地,他在以较长边????为直径的半圆内种菜,他家养的一只羊平时拴在??处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
/
A.3??
B.4??
C.5??
D.6??
?5.一根水平放置的圆柱形输水管道的横截面如图所示,其中有水部分水面宽0.4米,最深处水深0.1米,则此输水管道的直径等于( )
/
A.0.2米
B.0.25米
C.0.4米
D.0.5米
?6.已知:如图,△??????中,∠??=
60
°
,????为定长,以????为直径的⊙??分别交????、????于点??、??.连接????、????.下列结论:①????=2????;②??点到????的距离不变;③????+????=2????;④????为外接圆的切线.其中正确的结论是( )
/
A.①②
B.③④
C.①②③
D.①②④
?7.如图,在⊙0中,??为弧??????的中点,????⊥????交⊙0于??,若????=????=1,????的长为( )
/
A.2.5
B.3
C.3.5
D.4
?8.在直角坐标系中,以原点为圆心,4为半径作圆,该圆上到直线??=???+
2
的距离等于2的点共有( )
A.1个
B.2个
C.3个
D.4个
?9.如图,⊙??的半径为1,????是⊙??的一条弦,且????=
3
,则弦????所对圆周角的度数为( )
/
A.
30
°
B.
60
°
C.
30
°
或
150
°
D.
60
°
或
120
°
?10.如图,△??????的????边与⊙??相切于??点,若直径????=????=4,则????的值是( )
/
A.2
2
B.2
3
C.4
2
D.4
3
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,△??????中,∠??=
25
°
,∠??=
85
°
,过点??、??的圆交边????、????分别于点??、??,则∠??????=________
°
.
/ / /
?12.⊙
??
1
与⊙
??
2
相交于??、??,若
??
1
??
2
=7????,????=6????,⊙
??
1
的半径为5????,则⊙
??
2
的半径为________.
?13.已知:如图,三角形??????内接于⊙??,????为直径,过点??作直线????,要使得????是⊙??的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
?14.如图,????为⊙??的弦,直径????为4,????⊥????于??,∠??=
30
°
,则
????
的长为________(结果保留??).
?15.如图,以△??????的直角边????为直径的半圆??与斜边????交于点??,??是????边的中点.若????、????的长是方程
??
2
?6??+8=0的两个根,则图中阴影部分的面积为________.
/ / /
?16.如图,??是半径为2的⊙??外一点,????=4,????是⊙??的切线,点??是切点,弦?????//?????,连接????,则图中阴影部分的面积为________.
?17.如图,从半径为10????的圆形纸片上剪去
1
5
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为________.
18.一个直角三角形的两条边长是方程
??
2
?7??+12=0的两个根,则此直角三角形的外接圆的面积为________.
?19.如图,将半径为1、圆心角为
60
°
的扇形纸片??????,在直线??上向右作无滑动的滚动至扇形
??
′
??
′
??
′
处,则顶点??经过的路线总长为________.
/ /
?20.已知△??????的内切圆半径为??,∠??=
60
°
,????=2
3
,则??的取值范围是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,已知:△??????中,
(1)只用直尺(没有刻度)和圆规求作一点??,使点??到三角形各边的距离都相等(要求保留作图痕迹,不必写出作法).
(2)若△??????中,????=????=4,∠??????=
120
°
,那么请计算以△??????为轴截面的圆锥的侧面积(保留根号和??).
/
?
22.如图,在△??????中,∠??=
90
°
,∠??=
25
°
,以点??为圆心,????为半径的圆交????于点??,交????于点??,求
????
的度数.
/
?
23.如图,正方形????????的外接圆为⊙??,点??在劣弧
????
上(不与??点重合).
/
(1)求∠??????的度数;
(2)若⊙??的半径为8,求正方形????????的边长.
?
24.如图,以????为直径的⊙??经过????的中点??,????⊥????于点??.
/
(1)求证:????是⊙??的切线;
(2)当????=1,∠??=
30
°
时,求图中阴影部分的面积.
?
25.已知:??是⊙??外的一点,????=4,????交⊙??于点??,且??是????的中点,??是⊙??上任意一点.
/
(1)如图1,若????是⊙??的切线,求∠??????的大小;
(2)如图2,若∠??????=
90
°
,求????被⊙??截得的弦????的长.
?
26.????是⊙??的直径,????是⊙??的弦,过??作⊙??的切线,交????的延长线于??.作弦????,使∠??????=∠??????,连接????.
/
(1)求证:????是⊙??的切线;
(2)当∠??????=________
°
时,????⊥????,证明你的结论;
(3)????与????相交于??,当????=2,????=3时,求??到⊙??的切线长.
答案
1.A
2.C
3.C
4.B
5.D
6.A
7.B
8.D
9.D
10.C
11.70
12.
130
????或3
2
????
13.????⊥????∠??????=∠??∠??????+∠??????=
90
°
14.
2
3
??
15.4
3
?
4
3
??
16.
2
3
??
17.6????
18.4??或6.25??
19.
4
3
??
20.021.解:(1)作任意两角的角平分线,其交点即为所求作的点??.
/
(2)过??作????⊥????于??
/
∵????=????=4,∠??????=
120
°
∴由三角函数可得:????=2
3
∴??=4,??=2
3
∴??=??????=8
3
??.
22.解:连结????,如图,
/
∵∠??=
90
°
,∠??=
25
°
, ∴∠??=
90
°
?
25
°
=
65
°
, ∵????=????, ∴∠??=∠??????=
65
°
, ∴∠??????=
180
°
?
65
°
?
65
°
=
50
°
, ∴
????
的度数为
50
°
.
23.解:(1)连接????,????, ∵四边形????????为正方形, ∴∠??????=
90
°
, ∴∠??=
1
2
∠??????=
45
°
;
/
(2)过点??作????⊥????于点??, ∵????=????,∠??????=
90
°
, ∴∠??????=
45
°
, ∴????=????, ∵??
??
2
+??
??
2
=??
??
2
, ∴????=
??
??
2
2
=
64
2
=4
2
∴????=2????=2×4
2
=8
2
.
24.解:(1)连接????, ∵????是⊙??的直径,??是????的中点, ∴????是△??????的中位线, ∴?????//?????, ∵????⊥????, ∴????⊥????, ∵点??在圆上, ∴????为⊙??的切线;????
/
(2)∵∠??=
30
°
,????=1,∠??????=
90
°
, ∴????=2, ∵?????//?????, ∴∠??????=
30
°
, ∵????=????, ∴∠??????=∠??????=
30
°
, ∴∠??????=
120
°
, ∴????=
2
3
3
, ∴阴影部分面积??=
120???×(
2
3
3
)
2
360
?
1
2
×2×
3
3
=
4??
9
?
3
3
.
25.解:(1)如图1,∵????是⊙??的切线, ∴????⊥????,
/
∵??是????的中点, ∴????=2????, 在????△??????中,cos∠??????=
????
????
=
1
2
, ∴∠??????=
60
°
;(2)作????⊥????于??,如图2,则????=????, ∵∠??????=
90
°
,????=4,????=2, ∴????=
2
2
+
4
2
=2
5
, ∵∠??????=∠??????, ∴????△??????∽????△??????, ∴????:????=????:????,即????:2=2:2
5
, ∴????=
2
5
5
, ∴????=2????=
4
5
5
.
26.证明:(1)连接????,????; ∵????是圆的切线, ∴∠??????=
90
°
. ∵∠??????=∠??????, ∴∠??????=∠??????. ∵????=????,????=????, ∴△???????△??????. ∴∠??????=∠??????=
90
°
. ∴????是⊙??的切线.
/
(2)
45
°
. ∵∠??????=
90
°
, ∴四边形????????为正方形. ∴????⊥????.(3)根据题意,得圆的半径是5,则????=7, ∵????=????,∠??????=∠??????, ∴????垂直平分????. ∵?????????=?????????=21,????=????=
21
, 设????=??,????=??, 则有
??
2
=21+(3+??
)
2
??
2
=??(??+10)
, 解得
??=
5
2
21
??=7.5
, 即????=
5
2
21
.
