沪科版八年级数学上14.2.全等三角形的判定1SAS课件
文档属性
| 名称 | 沪科版八年级数学上14.2.全等三角形的判定1SAS课件 |  | |
| 格式 | zip | ||
| 文件大小 | 356.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-23 17:04:00 | ||
图片预览





文档简介
复习:
1.全等三角形的定义
2.全等三角形的性质
能完全重合的两个三角形,
叫做全等三角形。
全等三角形的对应边相等,
对应角相等。
14.2三角形全等的
判定(一)
阅读课本p97----100思考下列问题:
只知道三角形的一个元素能判定三角形全等吗?
知道两个元能判定三角形全等吗?
三角形的两边和夹角对应相等,三角形全等吗?
下面我们来探讨上面的问题
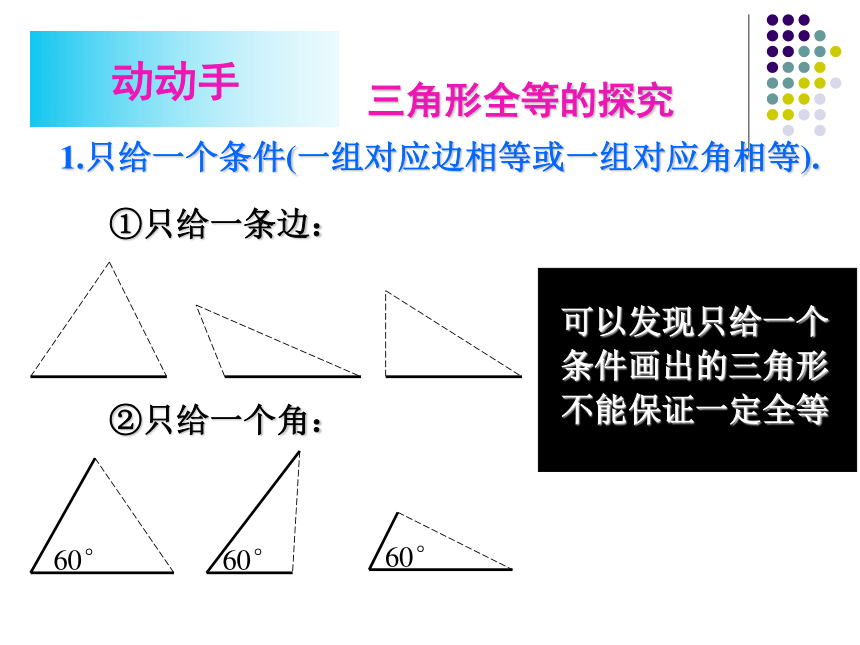
1.只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边:
②只给一个角:
60°
60°
60°
动动手
可以发现只给一个条件画出的三角形不能保证一定全等
三角形全等的探究
只给下面两个元素,能确定三角形的形状和大小吗?
(1)两条边长分别为4cm、2cm;
(2)一条边长为4cm,一个角为300
(3)两个角分别为450、300
动动手
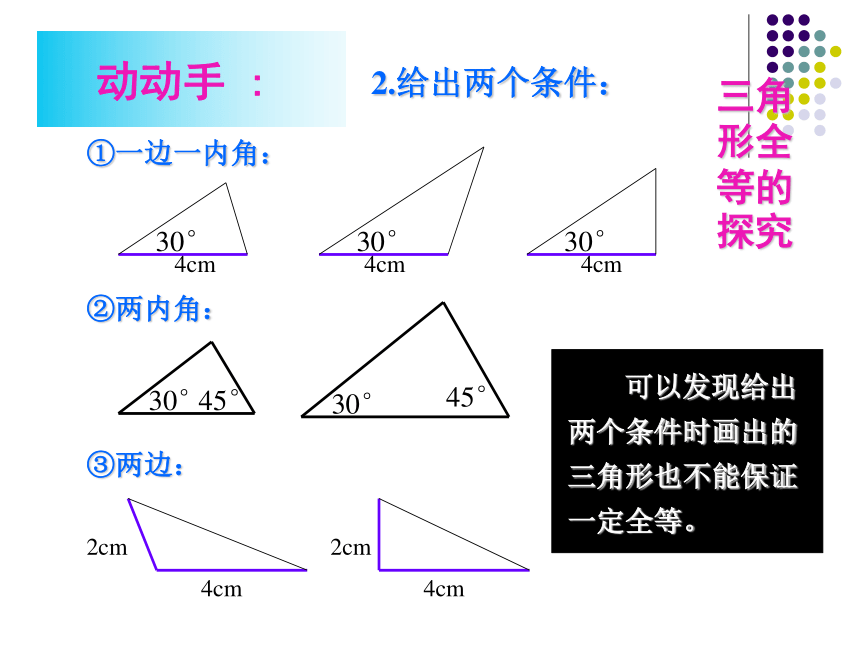
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
45°
45°
2cm
2cm
4cm
4cm
动动手 :
可以发现给出两个条件时画出的三角形也不能保证一定全等。
三角形全等的探究
4cm
4cm
4cm
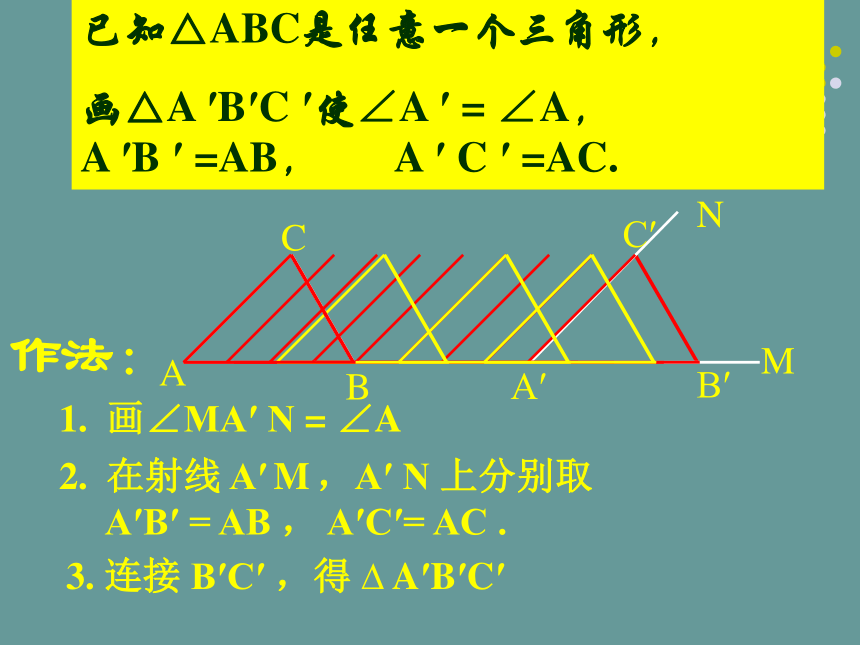
1. 画∠MA′ N = ∠A
A
B
C
M
N
A′
2. 在射线 A′ M ,A′ N 上分别取
A′B′ = AB , A′C′= AC .
B′
C′
3. 连接 B′C′ ,得 ? A′B′C′
已知△ABC是任意一个三角形,
画△A ′B′C ′使∠A ′ = ∠A, A ′B ′ =AB, A ′ C ′ =AC.
作法:
两三角形全等的判定方法一是如下的基本事实:
有两边和它们的夹角对应相等的
两个三角形全等.
可以简写成 “边角边” 或“ SAS ”
S ——边 A——角
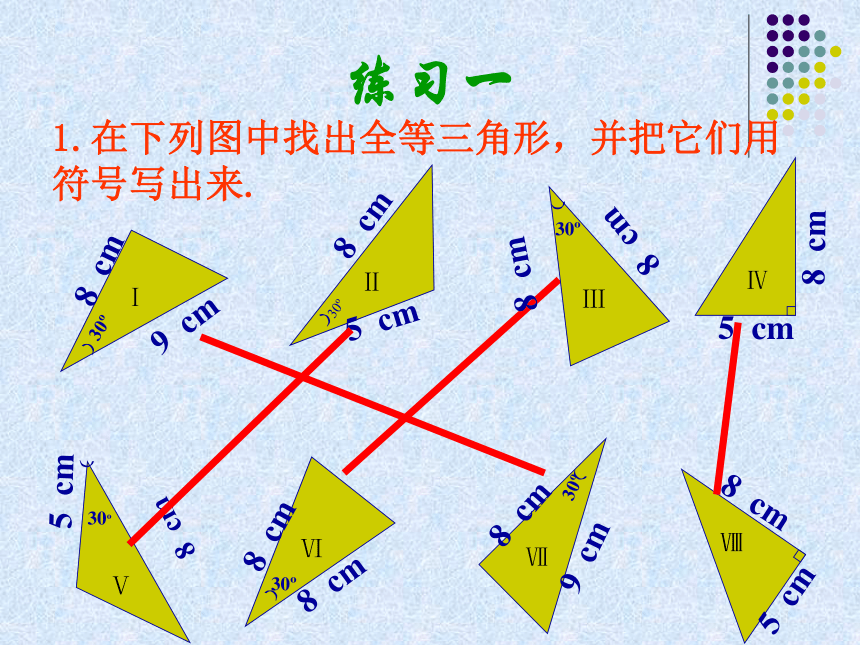
1.在下列图中找出全等三角形,并把它们用
符号写出来.
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30?
?
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
C
B
D
O
2.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
A
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB
这两个条件够吗?
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
还要一条边
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
它既是△ACB的一条边,
看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和△ADB中
AC = A D
∠CAB=∠DAB
A B = A B (公共边)
∴△ACB≌△ADB
(SAS)
(3)∠B=∠C
例2 已知如图,AB=AC,BE=CD。
试说明
(1)△ABD≌△ACE
(2)BD=CE
问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?说说你这样设计的理由。
A
B
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
△ABD≌ △ACD
S
A
S
练习二
2.如图,要证△ACB≌ △ADB ,至少选用哪些条件?
A
B
C
D
△ACB≌ △ADB
S
A
S
AB=AB
∠CAB= ∠ DAB
AC=AD
2.如图,要证△ACB≌ △ADB ,至少选用哪些条件?
A
B
C
D
△ACB≌ △ADB
S
A
S
AB=AB
∠CBA= ∠ DBA
BC=BD
课堂小结
1.边角边公理:有两边和它们的______对应相
等的两个三角形全等(SAS)
夹角
2.边角边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
1.证明两个三角形全等所需的条件应按对应边、对应
角、对应边顺序书写.
2.公理中所出现的边与角必须在所证明的两个三角形中.
3.公理中涉及的角必须是两边的夹角.
用公理证明两个三角形全等需注意
A
B
C
D
E
F
思考题:有两边和其中一边的对角对应相等的两个三角形是否全等。
作业布置: P100练习1,2,3.
谢谢,再见!
1.全等三角形的定义
2.全等三角形的性质
能完全重合的两个三角形,
叫做全等三角形。
全等三角形的对应边相等,
对应角相等。
14.2三角形全等的
判定(一)
阅读课本p97----100思考下列问题:
只知道三角形的一个元素能判定三角形全等吗?
知道两个元能判定三角形全等吗?
三角形的两边和夹角对应相等,三角形全等吗?
下面我们来探讨上面的问题
1.只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边:
②只给一个角:
60°
60°
60°
动动手
可以发现只给一个条件画出的三角形不能保证一定全等
三角形全等的探究
只给下面两个元素,能确定三角形的形状和大小吗?
(1)两条边长分别为4cm、2cm;
(2)一条边长为4cm,一个角为300
(3)两个角分别为450、300
动动手
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
45°
45°
2cm
2cm
4cm
4cm
动动手 :
可以发现给出两个条件时画出的三角形也不能保证一定全等。
三角形全等的探究
4cm
4cm
4cm
1. 画∠MA′ N = ∠A
A
B
C
M
N
A′
2. 在射线 A′ M ,A′ N 上分别取
A′B′ = AB , A′C′= AC .
B′
C′
3. 连接 B′C′ ,得 ? A′B′C′
已知△ABC是任意一个三角形,
画△A ′B′C ′使∠A ′ = ∠A, A ′B ′ =AB, A ′ C ′ =AC.
作法:
两三角形全等的判定方法一是如下的基本事实:
有两边和它们的夹角对应相等的
两个三角形全等.
可以简写成 “边角边” 或“ SAS ”
S ——边 A——角
1.在下列图中找出全等三角形,并把它们用
符号写出来.
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30?
?
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
C
B
D
O
2.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
A
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB
这两个条件够吗?
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
还要一条边
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
它既是△ACB的一条边,
看看线段AB
又是△ADB的一条边
△ACB 和△ADB的公共边
例1
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和△ADB中
AC = A D
∠CAB=∠DAB
A B = A B (公共边)
∴△ACB≌△ADB
(SAS)
(3)∠B=∠C
例2 已知如图,AB=AC,BE=CD。
试说明
(1)△ABD≌△ACE
(2)BD=CE
问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?说说你这样设计的理由。
A
B
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
△ABD≌ △ACD
S
A
S
练习二
2.如图,要证△ACB≌ △ADB ,至少选用哪些条件?
A
B
C
D
△ACB≌ △ADB
S
A
S
AB=AB
∠CAB= ∠ DAB
AC=AD
2.如图,要证△ACB≌ △ADB ,至少选用哪些条件?
A
B
C
D
△ACB≌ △ADB
S
A
S
AB=AB
∠CBA= ∠ DBA
BC=BD
课堂小结
1.边角边公理:有两边和它们的______对应相
等的两个三角形全等(SAS)
夹角
2.边角边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
1.证明两个三角形全等所需的条件应按对应边、对应
角、对应边顺序书写.
2.公理中所出现的边与角必须在所证明的两个三角形中.
3.公理中涉及的角必须是两边的夹角.
用公理证明两个三角形全等需注意
A
B
C
D
E
F
思考题:有两边和其中一边的对角对应相等的两个三角形是否全等。
作业布置: P100练习1,2,3.
谢谢,再见!
