1.2.2 函数的表示方法(第1课时)
文档属性
| 名称 | 1.2.2 函数的表示方法(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-23 15:38:49 | ||
图片预览






文档简介
1.2.2 函数的表示方法
(第1课时)
回顾旧知:
作业讲评P24 A组 第1题
(1)格式;
(2)定义域是一个集合
随练
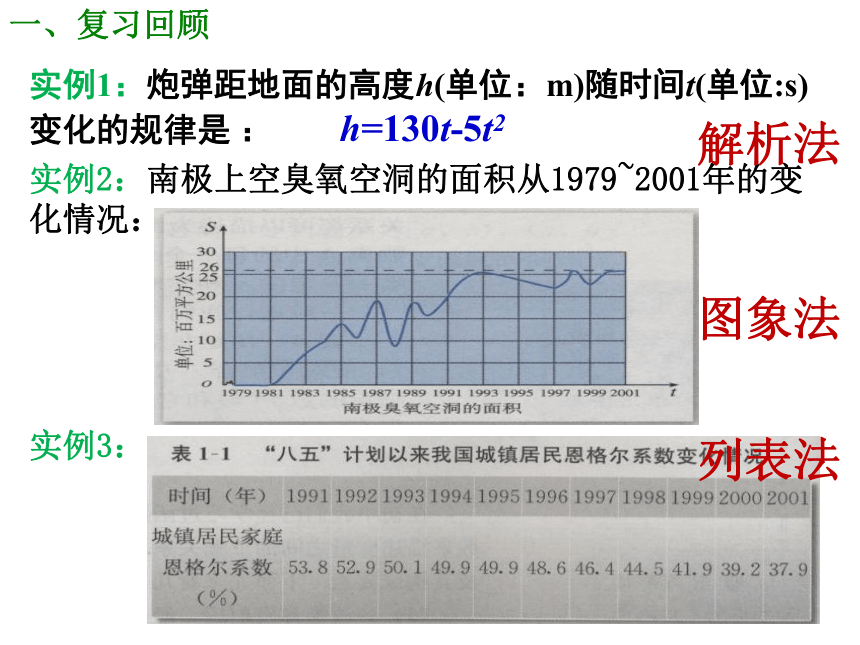
一、复习回顾
实例1:炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是 : h=130t-5t2
实例2:南极上空臭氧空洞的面积从1979~2001年的变化情况:
实例3:
解析法
图象法
列表法
⑶列表法:列出表格来表示两个变量的函数关系。
优点:不需要计算就可以直接看出与自变量相对应的函数值。
⑵图象法:用函数图象表示两个变量之间的关系。
优点:直观形象地表示随着自变量的变化,相应函数值的
变化趋向。
⑴解析法:用数学表达式表示两个变量之间的对应关系。
优点:①简明、全面地概括了变量间的关系;
②可通过解析式求出每个自变量对应的函数值。
二、基础知识讲解
常用的函数的三种表示法各自的优点
例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .
分析: “y=f (x)”可以用哪三种方法表示?.
三、例题分析
它可以是解析式,可以是图象,也可以是表格.
例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .
解:
用解析法可将函数 y=f (x)表示为:
用列表法可将函数 y=f (x)表示为:
用图象法可将函数 y=f (x)表示为:
, x∈{1 , 2 , 3 , 4 , 5 }
笔记本数 x
钱数 y
1 2 3 4 5
5 10 15 20 25
三、例题分析
y=5x
思考1:
若例1中的函数y=f(x)的定义域改为 [1,5],则其将图象会发生怎样的变化?
一条线段
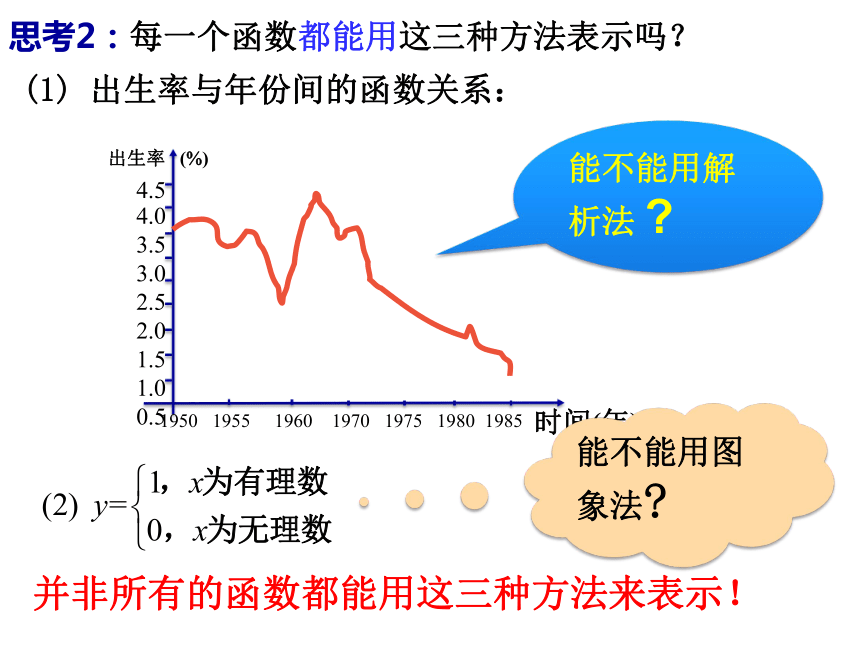
(1) 出生率与年份间的函数关系:
并非所有的函数都能用这三种方法来表示!
思考2:每一个函数都能用这三种方法表示吗?
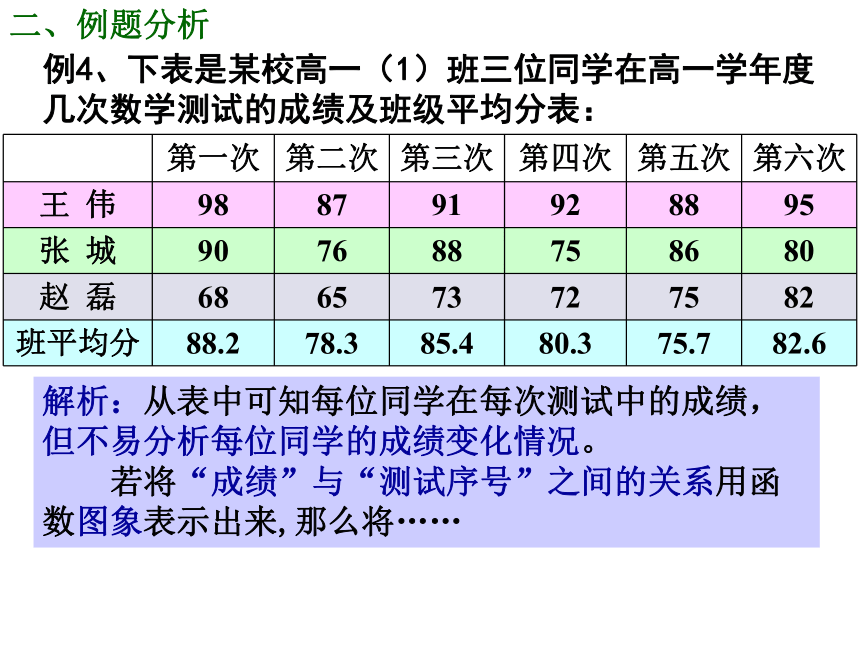
例4、下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:
请你对这三个同学在高一学年度的数学学习情况做一个分析.
解析:从表中可知每位同学在每次测试中的成绩,但不易分析每位同学的成绩变化情况。
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将……
二、例题分析
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,直观反映成绩变化:
虚线部分并不是图象的一部分
解:
由绝对值的概念可得:
列表:
建立坐标系作出图象如右所示
例5、画出函数 y = | x |的图象。
二、例题分析
0
0
1
1
-2
2
-1
1
列表
描点
连线
x
y
思考2:
函数图象可以是连续的曲线,也可以是直线、折线、离散的点等等;那么,如何判断在坐标平面中的图象是否为函数图象呢?
随练:下列四个图象中,不是函数图象的是( )
B
←任意性、唯一性
A
B
C
D
例6、某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数图象。
2
5
4
3
分段函数概念
解:设里程为x公里,票价为y元,
里程 x
票价 y
2
5
4
3
如何写出解析式?
解:设里程为x公里,票价为y元,
则可得函数解析式为
函数图象如右:
分段函数概念
里程 x
票价 y
1、分段函数:
一、基础知识讲解
在定义域中,对于自变量x的不同取值范围,对应关系不同,这样的函数称为分段函数.
1、分段函数:
一、基础知识讲解
(1)分段函数是一个函数,其定义域是各段“x取值范围”的并集,其值域是各段“y的取值范围”的并集。(定义域的区间端点需不重不漏!)
(2)求分段函数的函数值时,自变量的取值范围在哪一段,就用哪一段的解析式。
(3)研究分段函数时,应根据“先分后合”的原则,特别是画图象时,应先将各段函数图象画出,从而得到整个函数的图象。(注意端点“实心”还是“空心”)
配套练习:画出函数 y = | x-3 |的图象。
二、例题分析
解:由绝对值的概念可得:
列表:
建立坐标系作出图象如右所示
3
0
4
1
1
2
2
1
x
y
课本P23
1. 如图,把截面半径为25 cm 的圆形木头锯成矩形木料,如果矩形的一边长为x, 面积为 y ,把 y表示为x的函数。
必须注明
函数的定义域.
六、针对性练习
2、下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写一件事.
(1) 我离家不久, 发现自己把作业本放在家里了,于是返回家找到作业本再上学;
(2) 我骑着车一路匀速行驶, 只是再途中遇到一次交通堵塞, 耽搁了一些时间;
(3) 我出发后, 心情轻松, 缓缓行进, 后来为了赶时间开始加速.
A
B
D
思考题:画出下列函数的图象:
比较上面两个函数的图象,思考函数y=f(x)和y=|f(x)|图象的关系?
A:澄中所有学生组成的集合
B:澄中所有班级组成的集合
f:学生找班级
A B
f
C:澄中106班同学组成的集合
D:澄中高一各班级组成的集合
g:学生找班级
C D
g
映射概念
数集
集合
每一个数
每一个元素
唯一的数
唯一的元素
1、映射的概念
设A、B是两个非空的集合,如果按某一个确定的对应关系 f,使对于集合A中的任意一个元素 x,在集合B中都有唯一确定的元素 y 与之对应,那么就称对应 f: A→B 为从集合A到集合B的一个映射。
函数与映射有什么关系呢?
2、映射与函数关系
函数一定是映射;映射不一定是函数!
映射是函数的推广,即是将函数中的两个数集推广为两个任意集合。
函数:设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,就称f: A→B为从集合A到集合B的一个函数,记作:
y=f(x) , x∈A
映射概念
A:澄中所有学生组成的集合
B:澄中所有班级组成的集合
f:学生找班级
f : A B
C:澄中107班同学组成的集合
D:澄中高一各班级组成的集合
g:学生找班级
g : C D
A={P | P是平面直角坐标系内的点}
B={(x,y) | x ∈ R,y ∈ R}
f’:平面直角坐标系内的点跟它的坐标对应
f’ : E F
允许D中元素不存在对应元素
映射概念
1、下列对应中,能构成映射的有( )
非空集合、
唯一确定的对应关系、
任意x、
唯一确定的y
映射概念
2、已知集合A={a ,b},集合B={c,d},由集合A到集合B的映射有哪些?
解:设集合A到集合B之间的对应关系为f,则A到B之间的映射有以下几种情况:
(1) f(a)=c, f(b)=c;
(2) f(a)=d, f(b)=d;
(3) f(a)=c, f(b)=d;
(4) f(a)=d, f(b)=c;
映射概念
练习:P24 A组 第10题
P23 练习4
一、必做题
1、P24 习题1.2 A组 第7题
2、画图象并求值域:
六、作业
思考题:P25 B组 第3题
(第1课时)
回顾旧知:
作业讲评P24 A组 第1题
(1)格式;
(2)定义域是一个集合
随练
一、复习回顾
实例1:炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是 : h=130t-5t2
实例2:南极上空臭氧空洞的面积从1979~2001年的变化情况:
实例3:
解析法
图象法
列表法
⑶列表法:列出表格来表示两个变量的函数关系。
优点:不需要计算就可以直接看出与自变量相对应的函数值。
⑵图象法:用函数图象表示两个变量之间的关系。
优点:直观形象地表示随着自变量的变化,相应函数值的
变化趋向。
⑴解析法:用数学表达式表示两个变量之间的对应关系。
优点:①简明、全面地概括了变量间的关系;
②可通过解析式求出每个自变量对应的函数值。
二、基础知识讲解
常用的函数的三种表示法各自的优点
例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .
分析: “y=f (x)”可以用哪三种方法表示?.
三、例题分析
它可以是解析式,可以是图象,也可以是表格.
例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .
解:
用解析法可将函数 y=f (x)表示为:
用列表法可将函数 y=f (x)表示为:
用图象法可将函数 y=f (x)表示为:
, x∈{1 , 2 , 3 , 4 , 5 }
笔记本数 x
钱数 y
1 2 3 4 5
5 10 15 20 25
三、例题分析
y=5x
思考1:
若例1中的函数y=f(x)的定义域改为 [1,5],则其将图象会发生怎样的变化?
一条线段
(1) 出生率与年份间的函数关系:
并非所有的函数都能用这三种方法来表示!
思考2:每一个函数都能用这三种方法表示吗?
例4、下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:
请你对这三个同学在高一学年度的数学学习情况做一个分析.
解析:从表中可知每位同学在每次测试中的成绩,但不易分析每位同学的成绩变化情况。
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将……
二、例题分析
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,直观反映成绩变化:
虚线部分并不是图象的一部分
解:
由绝对值的概念可得:
列表:
建立坐标系作出图象如右所示
例5、画出函数 y = | x |的图象。
二、例题分析
0
0
1
1
-2
2
-1
1
列表
描点
连线
x
y
思考2:
函数图象可以是连续的曲线,也可以是直线、折线、离散的点等等;那么,如何判断在坐标平面中的图象是否为函数图象呢?
随练:下列四个图象中,不是函数图象的是( )
B
←任意性、唯一性
A
B
C
D
例6、某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数图象。
2
5
4
3
分段函数概念
解:设里程为x公里,票价为y元,
里程 x
票价 y
2
5
4
3
如何写出解析式?
解:设里程为x公里,票价为y元,
则可得函数解析式为
函数图象如右:
分段函数概念
里程 x
票价 y
1、分段函数:
一、基础知识讲解
在定义域中,对于自变量x的不同取值范围,对应关系不同,这样的函数称为分段函数.
1、分段函数:
一、基础知识讲解
(1)分段函数是一个函数,其定义域是各段“x取值范围”的并集,其值域是各段“y的取值范围”的并集。(定义域的区间端点需不重不漏!)
(2)求分段函数的函数值时,自变量的取值范围在哪一段,就用哪一段的解析式。
(3)研究分段函数时,应根据“先分后合”的原则,特别是画图象时,应先将各段函数图象画出,从而得到整个函数的图象。(注意端点“实心”还是“空心”)
配套练习:画出函数 y = | x-3 |的图象。
二、例题分析
解:由绝对值的概念可得:
列表:
建立坐标系作出图象如右所示
3
0
4
1
1
2
2
1
x
y
课本P23
1. 如图,把截面半径为25 cm 的圆形木头锯成矩形木料,如果矩形的一边长为x, 面积为 y ,把 y表示为x的函数。
必须注明
函数的定义域.
六、针对性练习
2、下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写一件事.
(1) 我离家不久, 发现自己把作业本放在家里了,于是返回家找到作业本再上学;
(2) 我骑着车一路匀速行驶, 只是再途中遇到一次交通堵塞, 耽搁了一些时间;
(3) 我出发后, 心情轻松, 缓缓行进, 后来为了赶时间开始加速.
A
B
D
思考题:画出下列函数的图象:
比较上面两个函数的图象,思考函数y=f(x)和y=|f(x)|图象的关系?
A:澄中所有学生组成的集合
B:澄中所有班级组成的集合
f:学生找班级
A B
f
C:澄中106班同学组成的集合
D:澄中高一各班级组成的集合
g:学生找班级
C D
g
映射概念
数集
集合
每一个数
每一个元素
唯一的数
唯一的元素
1、映射的概念
设A、B是两个非空的集合,如果按某一个确定的对应关系 f,使对于集合A中的任意一个元素 x,在集合B中都有唯一确定的元素 y 与之对应,那么就称对应 f: A→B 为从集合A到集合B的一个映射。
函数与映射有什么关系呢?
2、映射与函数关系
函数一定是映射;映射不一定是函数!
映射是函数的推广,即是将函数中的两个数集推广为两个任意集合。
函数:设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,就称f: A→B为从集合A到集合B的一个函数,记作:
y=f(x) , x∈A
映射概念
A:澄中所有学生组成的集合
B:澄中所有班级组成的集合
f:学生找班级
f : A B
C:澄中107班同学组成的集合
D:澄中高一各班级组成的集合
g:学生找班级
g : C D
A={P | P是平面直角坐标系内的点}
B={(x,y) | x ∈ R,y ∈ R}
f’:平面直角坐标系内的点跟它的坐标对应
f’ : E F
允许D中元素不存在对应元素
映射概念
1、下列对应中,能构成映射的有( )
非空集合、
唯一确定的对应关系、
任意x、
唯一确定的y
映射概念
2、已知集合A={a ,b},集合B={c,d},由集合A到集合B的映射有哪些?
解:设集合A到集合B之间的对应关系为f,则A到B之间的映射有以下几种情况:
(1) f(a)=c, f(b)=c;
(2) f(a)=d, f(b)=d;
(3) f(a)=c, f(b)=d;
(4) f(a)=d, f(b)=c;
映射概念
练习:P24 A组 第10题
P23 练习4
一、必做题
1、P24 习题1.2 A组 第7题
2、画图象并求值域:
六、作业
思考题:P25 B组 第3题
