12.2.1正比例函数的图象和性质课件 (共25张PPT)
文档属性
| 名称 | 12.2.1正比例函数的图象和性质课件 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-23 19:37:15 | ||
图片预览







文档简介
课件25张PPT。复习引入1、函数的概念
2、正比例的定义
本节课学习一类特殊的函数12.2一 次 函 数
第1课时 正比例函数的图象和性质 (1)h=30t+1800 (2)Q =-25t+300 (3)y=2x (4)y=- 2 x (5)s=80t (1)函数表达式都是用自变量的一次式表示的,观察上面的几个函数,在形式上它们有什么样的共同特征?(2)可以写成y=kx+b的整式形式K是一次项系数b是常数项 一般地,若两个变量 x、y之间的关系可以表示成y=kx+b (k,b是常数,且 k≠0)的函数,叫做一次函数。 当b=0时,y=kx+b就变成了 (k≠0)
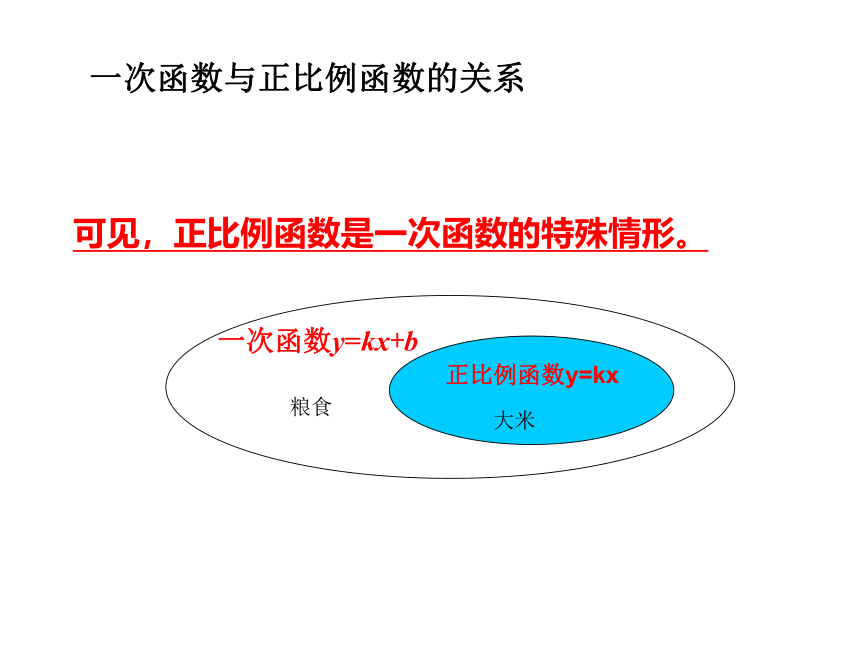
叫正比例函数 一次函数的定义:y=kx(1)自变量x的次数为1(2)比例系数k≠0(3)解析式是关于自变量的整式(举例) 可见,正比例函数是一次函数的特殊情形。
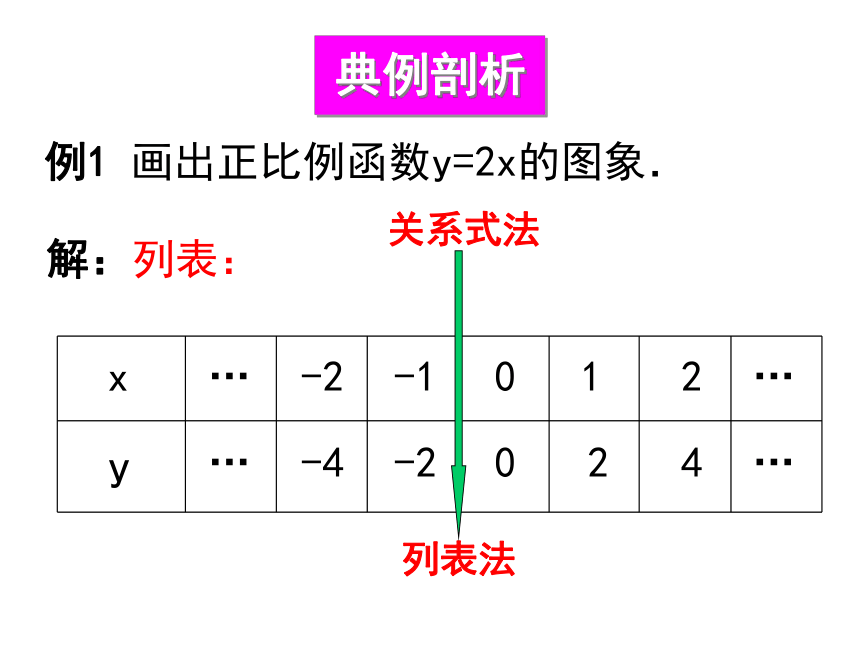
大米粮食一次函数与正比例函数的关系正比例函数y=kx一次函数y=kx+b下列函数中,哪些是一次函数?哪些是正比例函数?(1)和(4)是一次函数;(1) 是正比例函数.随堂演练如何画正比例函数的图像?前面画过y=2x.y=-2x及其它正比例函数的图像,例1 画出正比例函数y=2x的图象.解:列表:
xy100-12-2…………24-2-4关系式法列表法描点连线画函数图象的一般步骤有哪些?列表:y=2x动手操作,深化探索 (做一做 )(1)画出正比例函数y=-2x的图象.在同一个平面直角坐标系中 -5 -4 -3 -2 -154321-1 0-2-3-4-5 2 3 4 5y 1y=2xxy=-2x相同点:
不同点:函数y=2x的图象经过第 象限,从左向右 ,函数y=-2x的图象经过第 象
限.从左向右 。呈上升状态一、三呈下降状态二、四两图象都是经过原点的一条直线正比例函数y=kx的图象是一条经过原点的直线。因此,画正比例函数图象时,只要再确定一个点,过这点与原点画直线就可以了。为什么?两点法正比例函数y=kx的图象特征:小结: 正比例函数图象经过点(0,0)和点(1,k)正比例函数y=kx图像的画法两点法例1. 在同一平面直角坐标系中,画下列函数的图像:例题解析用两点法结合图像,就下面问题思考后回答:当k > 0时y = k x的图像在一、三象限且函数值也即y随 x 增加而增加练习1、在同一平面直角坐标系中,画下列函数的图像:yxk < 0时, y = k x的图像在二、四象限且函数值随 x 增加而减小.练习2. 结合下图及第1题中的图像,就下面问题思考后回答:(2) k > 0与k < 0时,y = k x的图像各有什么特点?k > 0时y = k x的图像在一、三象限且函数值随 x 增加而增加,k < 0时, y = k x的图像在二、四象限且函数值随 x 增加而减小.一般地,正比例函数y=kx(k是常数,k≠0)的图象我们称它为直线y=kx.正比例函数图象的特征及性质1、是一条经过原点的直线;结 论3、 越大直线y=kx就越陡也即越靠近y轴 越小直线y=kx就越平缓也即越靠近x轴1.下列函数中哪些是一次函数,哪些又是正比例函数?2.下列说法正确的是 填序号)
①正比例函数一定是一次函数;
②一次函数一定是正比例函数;
(3)若y=kx+b,则y是x的一次函数。① y=–8x (2)y= (3)y= (4)y= –0.5x+1 (5)y=(a2+1)x+3 (6)y=ax巩固练习:(7)x+2y=3 (8)y=- x (9)y=2(10)y=2(x+1)(11)y=2x2-(3x+2x2) B二、四0-3减小1. 正比例函数y=(m-1)x的图象经过一、三象限,A. m=1B. m>1C. m<1D. m≥13. 函数y=-3x的图象在第 象限内,经过点2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.
k>34. 函数y= x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .(0, )与点(1, ),y随x的增大而 .三、一0增大则m的取值范围是( )练一练写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为x 的正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程为y(千米)与行驶时间x(时)之间的关系; 解:由路程=速度×时间,得y=60x ,y是x的 一次函数,也是x的正比例函数.数学回归到生活实际 解:由圆的面积公式,得y= πx2, y不是x的一次函 数,也不是x的正比例函数. (2)圆的面积y ( 平方厘米 )与它的半径x
( 厘米)之间的关系 (3)某水池有水15立方米,现打开进水管进水,进水速度为5立方米/h,xh后这个水池内有水y立方米?解:这个水池每时增加5立方米的水,xh增加5x立方米的水,因而y=15+5x, y是x的一次函数,但不是x的正比例函数.2.某种大米的单价是2.2元/kg,当购买x kg大米时,花费为y元.y是x的一次函数吗?是正比例函数吗?解:由总价=单价×数量,得y=2.2x, y是x的一次函数,也是的正比例函数.1、函数与图象之间是一一对应的关系;2、正比例函数的图象是一条经过原点的直线;3、作正比例函数图象时,只取原点外的另一个点,就能很快作出;通过本节课,你有什么收获?1.从教材习题中选取,
2.完成练习册本课时的习题.
2、正比例的定义
本节课学习一类特殊的函数12.2一 次 函 数
第1课时 正比例函数的图象和性质 (1)h=30t+1800 (2)Q =-25t+300 (3)y=2x (4)y=- 2 x (5)s=80t (1)函数表达式都是用自变量的一次式表示的,观察上面的几个函数,在形式上它们有什么样的共同特征?(2)可以写成y=kx+b的整式形式K是一次项系数b是常数项 一般地,若两个变量 x、y之间的关系可以表示成y=kx+b (k,b是常数,且 k≠0)的函数,叫做一次函数。 当b=0时,y=kx+b就变成了 (k≠0)
叫正比例函数 一次函数的定义:y=kx(1)自变量x的次数为1(2)比例系数k≠0(3)解析式是关于自变量的整式(举例) 可见,正比例函数是一次函数的特殊情形。
大米粮食一次函数与正比例函数的关系正比例函数y=kx一次函数y=kx+b下列函数中,哪些是一次函数?哪些是正比例函数?(1)和(4)是一次函数;(1) 是正比例函数.随堂演练如何画正比例函数的图像?前面画过y=2x.y=-2x及其它正比例函数的图像,例1 画出正比例函数y=2x的图象.解:列表:
xy100-12-2…………24-2-4关系式法列表法描点连线画函数图象的一般步骤有哪些?列表:y=2x动手操作,深化探索 (做一做 )(1)画出正比例函数y=-2x的图象.在同一个平面直角坐标系中 -5 -4 -3 -2 -154321-1 0-2-3-4-5 2 3 4 5y 1y=2xxy=-2x相同点:
不同点:函数y=2x的图象经过第 象限,从左向右 ,函数y=-2x的图象经过第 象
限.从左向右 。呈上升状态一、三呈下降状态二、四两图象都是经过原点的一条直线正比例函数y=kx的图象是一条经过原点的直线。因此,画正比例函数图象时,只要再确定一个点,过这点与原点画直线就可以了。为什么?两点法正比例函数y=kx的图象特征:小结: 正比例函数图象经过点(0,0)和点(1,k)正比例函数y=kx图像的画法两点法例1. 在同一平面直角坐标系中,画下列函数的图像:例题解析用两点法结合图像,就下面问题思考后回答:当k > 0时y = k x的图像在一、三象限且函数值也即y随 x 增加而增加练习1、在同一平面直角坐标系中,画下列函数的图像:yxk < 0时, y = k x的图像在二、四象限且函数值随 x 增加而减小.练习2. 结合下图及第1题中的图像,就下面问题思考后回答:(2) k > 0与k < 0时,y = k x的图像各有什么特点?k > 0时y = k x的图像在一、三象限且函数值随 x 增加而增加,k < 0时, y = k x的图像在二、四象限且函数值随 x 增加而减小.一般地,正比例函数y=kx(k是常数,k≠0)的图象我们称它为直线y=kx.正比例函数图象的特征及性质1、是一条经过原点的直线;结 论3、 越大直线y=kx就越陡也即越靠近y轴 越小直线y=kx就越平缓也即越靠近x轴1.下列函数中哪些是一次函数,哪些又是正比例函数?2.下列说法正确的是 填序号)
①正比例函数一定是一次函数;
②一次函数一定是正比例函数;
(3)若y=kx+b,则y是x的一次函数。① y=–8x (2)y= (3)y= (4)y= –0.5x+1 (5)y=(a2+1)x+3 (6)y=ax巩固练习:(7)x+2y=3 (8)y=- x (9)y=2(10)y=2(x+1)(11)y=2x2-(3x+2x2) B二、四0-3减小1. 正比例函数y=(m-1)x的图象经过一、三象限,A. m=1B. m>1C. m<1D. m≥13. 函数y=-3x的图象在第 象限内,经过点2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.
k>34. 函数y= x的图象在第 象限内,经过点(0, )与点(1, ),y随x的增大而 .(0, )与点(1, ),y随x的增大而 .三、一0增大则m的取值范围是( )练一练写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为x 的正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程为y(千米)与行驶时间x(时)之间的关系; 解:由路程=速度×时间,得y=60x ,y是x的 一次函数,也是x的正比例函数.数学回归到生活实际 解:由圆的面积公式,得y= πx2, y不是x的一次函 数,也不是x的正比例函数. (2)圆的面积y ( 平方厘米 )与它的半径x
( 厘米)之间的关系 (3)某水池有水15立方米,现打开进水管进水,进水速度为5立方米/h,xh后这个水池内有水y立方米?解:这个水池每时增加5立方米的水,xh增加5x立方米的水,因而y=15+5x, y是x的一次函数,但不是x的正比例函数.2.某种大米的单价是2.2元/kg,当购买x kg大米时,花费为y元.y是x的一次函数吗?是正比例函数吗?解:由总价=单价×数量,得y=2.2x, y是x的一次函数,也是的正比例函数.1、函数与图象之间是一一对应的关系;2、正比例函数的图象是一条经过原点的直线;3、作正比例函数图象时,只取原点外的另一个点,就能很快作出;通过本节课,你有什么收获?1.从教材习题中选取,
2.完成练习册本课时的习题.
