沪科版八年级(上)第15章轴对称图形与等腰三角形测试题(含答案)
文档属性
| 名称 | 沪科版八年级(上)第15章轴对称图形与等腰三角形测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-24 18:44:30 | ||
图片预览

文档简介
轴对称图形与等腰三角形
一、选择题(共8小题,共24分)
图,矩形ABC中,E是D中点,将△BE沿直线B折叠后得△GBE,延长BG交点F.A=6,BC=4,则F的长为 )
A. 2 B. 4 C. D.
如图,在矩形ABCD中,BC=6,CD=3,将ABCD按对角线BD翻折,点C落在点C'处,BC'交AD于点E,则线段DE的长为( )
A. 3
B.
C. 5
D.
如图,在矩形ACD中AB=,BC=1,点E是C的中,连接A,将△BE沿E叠点B落在处,连接C,则in∠ECF=( )
A.
B.
C.
D.
如,矩形片BD中,B=4,BC=8,纸片沿F折叠,点C与点重,则下列结论错的是( )
A.
B. ≌
C.
D.
如图ABC是矩形纸,折∠B,∠D,使ADBC与对角AC重叠,且顶点B,D好落在一点O上,折痕别是EAF则等于( )
A.
B. 2
C.
D.
图,A和B地在一河的两岸,现要在上造一座桥MN,使从到的径MNB短的是(定河的两岸是平行直线,要岸垂)( )
A.
B.
C.
D.
如,在坐标,点A、B的坐分别为(1,4和30),点C是y轴上的一个动,且AB、C点在同一条直线上,当△ABC的最,点C的坐标是( )
A. B. C. D.
如,在平面角坐标系中,Rt△OB的顶A在x轴的正半上.点B坐标为(,),点C的标(,),点P为边B上的一个点,则PA+PC的最小值为 )
A. B. C. D.
二、填空题(共14题,共42分)
如图,平面直角坐标系中,将形OC沿线AE折叠(点在边DC上)折叠端点D恰落边OC上的点F处.若点D的坐标(,8),则点坐标为______.
如图,在形ABCD中D∥B,C=90°E为D上一点,分别EA,EB折将两个(∠D,C向内叠,点C,D恰好落AB边的点F处.若AD=2,=3则EF的长为______ .
如一张三角形片BC,AB=AC5.叠该纸片使点A落在边BC的中上,痕过C上的点E,线段E的长为______ .
如图,将矩形纸片AB叠,使点A与C重合折痕EF,AB=4,BC2,线段EF的长为______ .
如正形ABCD的长是2,∠DAC的平分线交DC于E,点、Q分别是AD和AE动点DQ+PQ的小值为______.
如图,在正方形ACD中,EAB上点,BE=,AE=3BEP是AC上点B+PE的最小值是______.
图方ABCD的边长为,点P在D边上且DP=1,Q是AC动点,DQ+PQ的最小值为______.
,在Rt△B中,C=90°,∠B=60°,点D是BC边上的点,CD,△AB直线AD翻折,使点CB边的点E处,若点P是直线AD上动点则△EB周长的小值是______.
如图,方ABCD的边长2,以正方形ABCD边A为边,在正内作等边三AEP为对角线AC上的点,PDPE的最小值为______.
在如所示的平面直角坐标系中,点P是线=x上的动点A(1,0(2,0)x轴上的两点PA+PB的最为______.
菱形ACD的边2,∠ABC=60°,EA中点,点P是对角线BD上的动点,当APPE的最,P的是______.
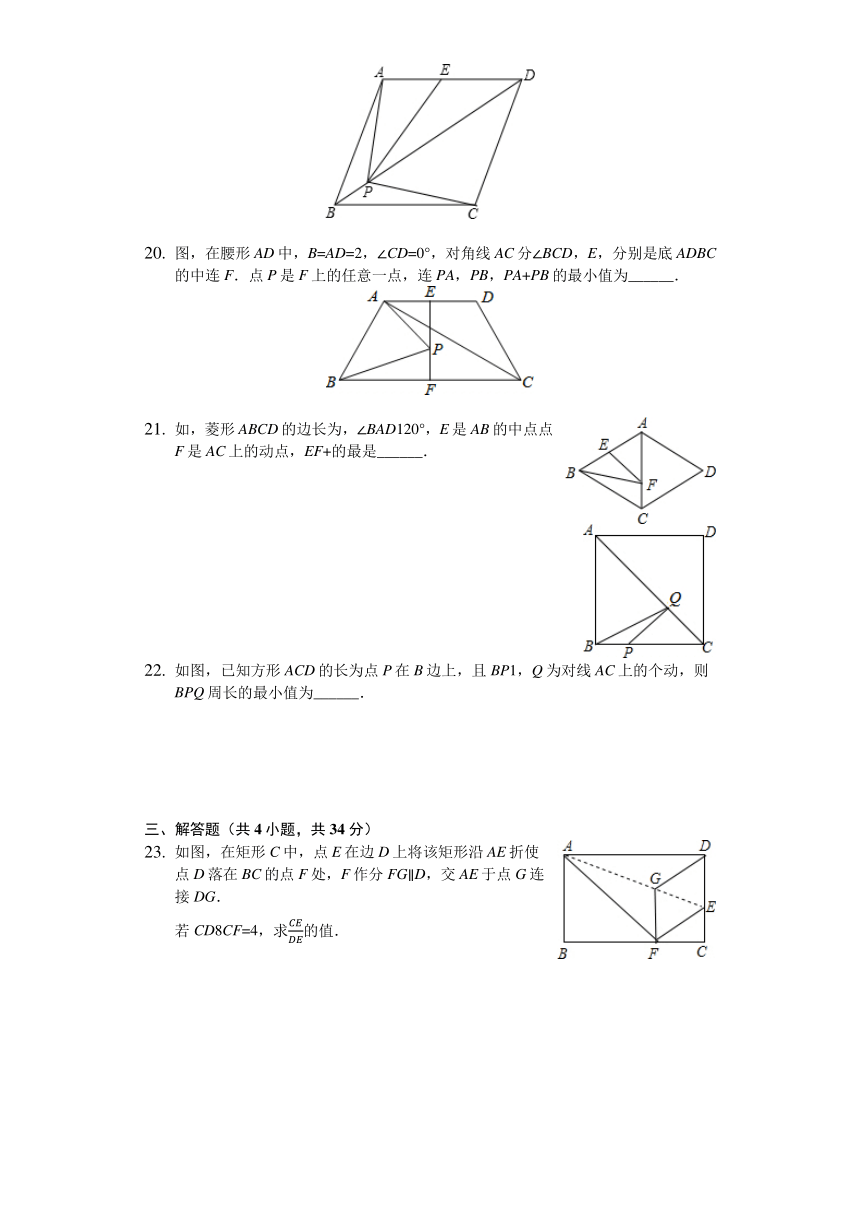
图,在腰形AD中,B=AD=2,∠CD=0°,对角线AC分∠BCD,E,分别是底ADBC的中连F.点P是F上的任意一点,连PA,PB,PA+PB的最小值为______.
如,菱形ABCD的边长为,∠BAD120°,E是AB的中点点F是AC上的动点,EF+的最是______.
如图,已知方形ACD的长为点P在B边上,且BP1,Q为对线AC上的个动,则BPQ周长的最小值为______.
三、解答题(共4小题,共34分)
如图,在矩形C中,点E在边D上将该矩形沿AE折使点D落在BC的点F处,F作分FG∥D,交AE于点G连接DG.
若CD8CF=4,求的值.
如图已,的直径C为4,A⊙O上,∠ACD=30°B为AD的中点,为直径CD上一动,则BP+AP的小值为______.
如,A、线l的同,要在直线l一C使ACBC的距离之和小,我们可以出点B于l的对称点B′,连AB′与直线l交于点C,则点C为所求.
实运用:
如图,在t△A中AB0,∠BAC=45°,∠BAC的平分线BC于,、F分是线段AD和AB上的动,求E+EF的小值,写出解过程.
如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.
如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.
答案
1.B
2.B
3.D
4.D
5.B
6.D
7.D
8.B
9.(10,3)
10.
11.2.5
12.
13.
14.10
15.5
16.1+
17.2
18.
19.
20.2
21.2
22.6
23.R△EC中,FC2EC2=EF2,
∴四形EFG为菱形;
解得:x=5,CE=8=,
∴DG=G=E=DE,
∴∠2=∠,
即4+(8-x)2x,
∵FGCD,
∴=.
24.2
解:作点B关于CD的对称点E,连交CD于,
∠AOD=60,∠E=30°,
如图斜边AC上截AB′AB,连结B′.
过点B′作B′F⊥AB,垂足F,A于E连BE,
∴△B′A△BA(SAS),
APBP的最小值是2.
Rt△AB′中,∠BA=4°,AB′=B=10,
∴B′FAB′?in45°=AB?sn°=1×=5,
作直径AC′连接′E.
∴∠C′E=4°,
,
∴∠O=90°,
则线B′的长即为所求
又AC′圆直径,∴∠EC=90°,
此时A+PB最小,等于A.
∴∠BAM=BAM,
据垂径定理得=.
在B′AM和△BA中
∴C′=AE=AC=2,
BE+EF的最值为.
找点A或B于CD的对称点,再连接其中点的对点和另一点,CD的交就所求作的位置.据题意先求出∠′AE,据股理求A,即可得出PA+PB的小值;
25.解:∵AD平分∠BAC
∴∠BAD=∠DAE,
∵∠BAD=29°,
∴∠DAE=29°,
∴∠BAC=58°,
∵DE垂直平分AC,
∴AD=DC,
∴∠DAE=∠DCA=29°,
∵∠BAC+∠DCA+∠B=180°,
∴∠B=93°.
26.证明:连接BD,DC,如图:
∵DE所在直线是BC的垂直平分线,
∴BD=CD,
∵AD平分∠BAC,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N,
∴DM=DN,
在Rt△BMD与Rt△CDN中,
,
∴Rt△BMD≌Rt△CDN(HL),
∴BM=CN;
