人教版八年级数学上册12.3角的平分线的性质选择填空基础练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质选择填空基础练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 233.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-25 10:50:39 | ||
图片预览



文档简介
《12.3 角的平分线的性质》选择、填空练习
时间:45分钟 总分:60
一、选择题(本大题共12小题,共36.0分)
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A. 6 B. 5 C. 4 D. 3
如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E,BC=5,DE=2,则△BCE的面积等于()
A. 10
B. 7
C. 5
D. 4
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B. 2 C. 3 D.
如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
A. 2
B.
C.
D.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,AC=3,BC=4,则CD的长是( )
?
A. 1 B. C. D. 2
如图,AD是△ABC的角平分线,则AB:AC等于( )
A. BD:CD
B. AD:CD
C. BC:AD
D. BC:AC
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
①OA=OD;
②AD⊥EF;
③当∠A=90°时,四边形AEDF是正方形;
④AE2+DF2=AF2+DE2.
其中正确的是( )
A. B. C. D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
?①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A. 1 B. 2 C. 3 D. 4
如图,三角形ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E,F,下面四个结论:
①∠AFE=∠AEF;
②AD垂直平分EF;
③;
④EF一定平行BC.
其中正确的是( )
A.
B.
C.
D.
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A. 3 B. 4 C. 6 D. 5
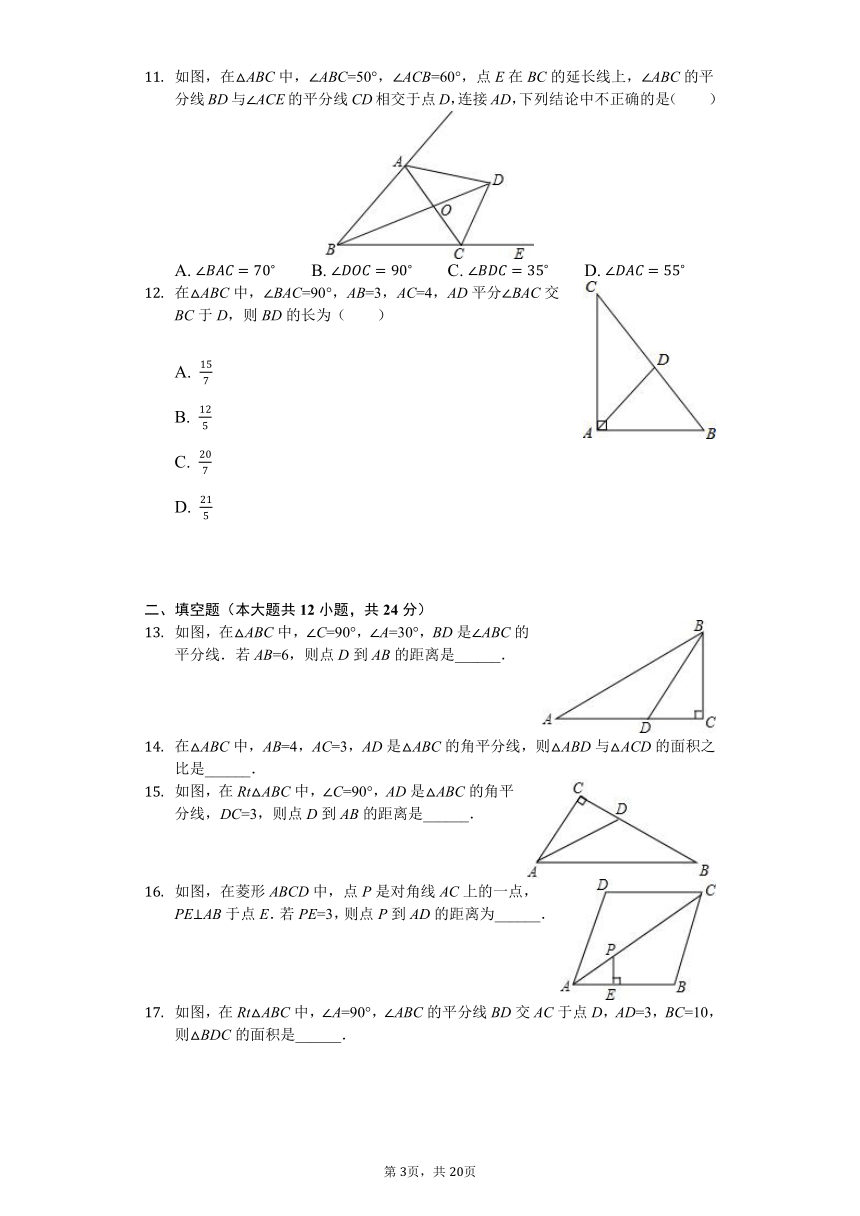
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )
A. B. C. D.
在△ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为( )
A.
B.
C.
D.
二、填空题(本大题共12小题,共24分)
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是______.
在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是______.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是______.
如图,在菱形ABCD中,点P是对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为______.
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是______.
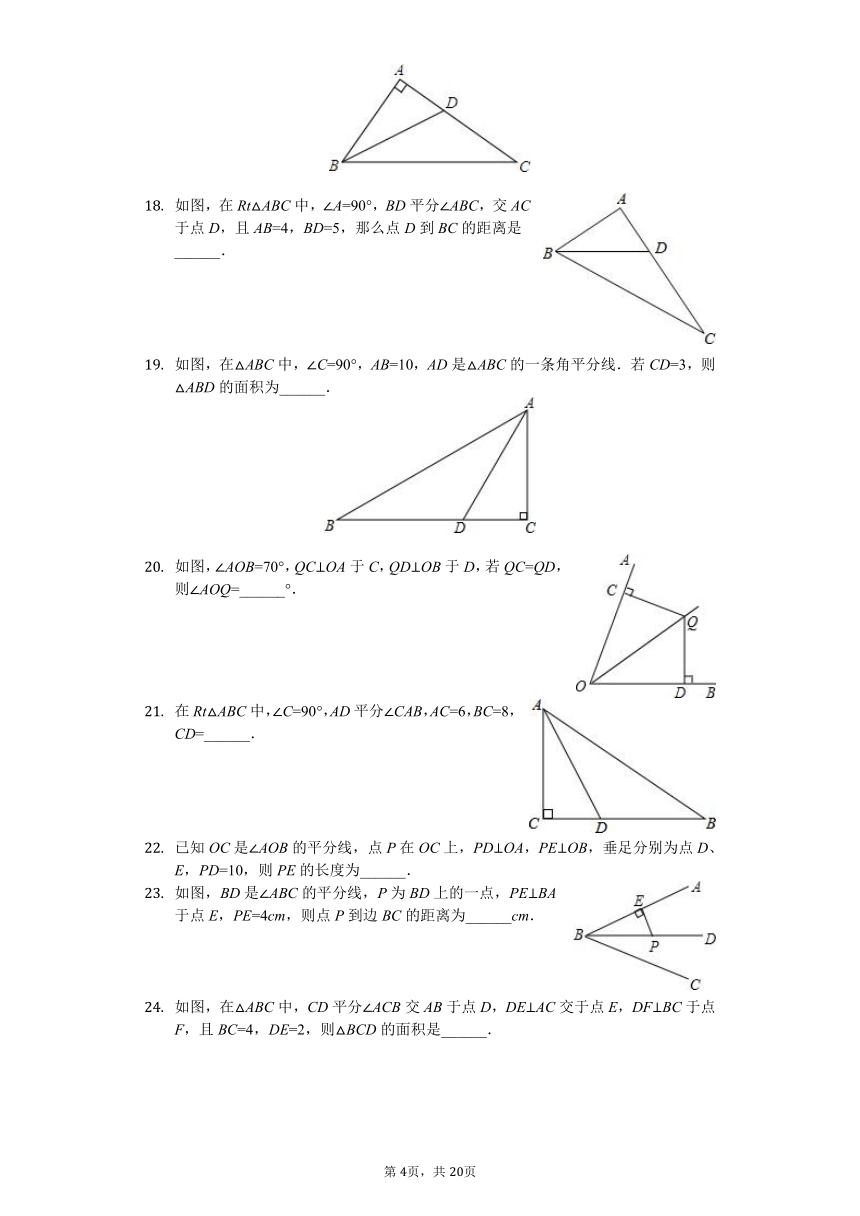
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,那么点D到BC的距离是______.
如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为______.
如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ=______°.
在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=______.
已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D、E,PD=10,则PE的长度为______.
如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA于点E,PE=4cm,则点P到边BC的距离为______cm.
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是______.
答案和解析
1.【答案】A
【解析】
解:如图,
过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PD=6,
∴PE=6,
即点P到OB的距离是6.
故选:A.
过点P作PE⊥OB于点E,根据角平分线上的点到角的两边的距离相等可得PE=PD,从而得解.
本题考查了角平分线上的点到角的两边的距离相等的性质,是基础题,比较简单,熟记性质是解题的关键.
2.【答案】C
【解析】
解:作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=BC?EF=×5×2=5,
故选:C.
作EF⊥BC于F,根据角平分线的性质求得EF=DE=2,然后根据三角形面积公式求得即可.
本题考查了角的平分线的性质以及三角形的面积,作出辅助线求得三角形的高是解题的关键.
3.【答案】C
【解析】
解:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故选:C.
根据角平分线的性质即可求得CD的长,然后在直角△BDE中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.
本题考查了角的平分线的性质以及直角三角形的性质,30°的锐角所对的直角边等于斜边的一半,理解性质定理是关键.
4.【答案】C
【解析】
解:∵OP平分∠AOB,∠AOB=60°,
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE=CP=1,
∴PE==,
∴OP=2PE=2,
∵PD⊥OA,点M是OP的中点,
∴DM=OP=.
故选:C.
由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性质,即可求得PE的值,继而求得OP的长,然后由直角三角形斜边上的中线等于斜边的一半,即可求得DM的长.
此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质.此题难度适中,注意掌握数形结合思想的应用.
5.【答案】C
【解析】
?解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD是△ABC的角平分线,
∴DE=CD,
由勾股定理得,AB===5,
S△ABC=AB?DE+AC?CD=AC?BC,
即×5?CD+×3?CD=×3×4,
解得CD=.
故选C.
过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,利用勾股定理列式求出AB,再根据△ABC的面积公式列出方程求解即可.
本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,勾股定理,熟记性质并根据三角形的面积列出方程是解题的关键.
6.【答案】A
【解析】
解:如图
过点B作BE∥AC交AD延长线于点E,
∵BE∥AC,
∴∠DBE=∠C,∠E=∠CAD,
∴△BDE∽△CDA,
∴=,
又∵AD是角平分线,
∴∠E=∠DAC=∠BAD,
∴BE=AB,
∴=,
∴AB:AC=BD:CD.
故选:A.
先过点B作BE∥AC交AD延长线于点E,由于BE∥AC,利用平行线分线段成比例定理的推论、平行线的性质,可得∴△BDE∽△CDA,∠E=∠DAC,再利用相似三角形的性质可有=,而利用AD时角平分线又知∠E=∠DAC=∠BAD,于是BE=AB,等量代换即可证.
此题考查了角平分线的定义、相似三角形的判定和性质、平行线分线段成比例定理的推论.关键是作平行线.
7.【答案】D
【解析】
解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD∠FAD,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,
∴④正确;
在△AEO和△AFO中,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴③正确.
综上,可得
正确的是:②③④.
故选:D.
①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确.
②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF.
③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可.
④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE2+DF2=AF2+DE2成立.
(1)此题主要考查了三角形的角平分线的性质和应用,以及直角三角形的性质和应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和应用,要熟练掌握.
(3)此题还考查了矩形、正方形的性质和应用,要熟练掌握.
8.【答案】D
【解析】
解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=∠CAB=30°,
∴∠3=90°-∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD=AD,
∴BC=CD+BD=AD+AD=AD,S△DAC=AC?CD=AC?AD.
∴S△ABC=AC?BC=AC?AD=AC?AD,
∴S△DAC:S△ABC=AC?AD:AC?AD=1:3.
故④正确.
综上所述,正确的结论是:①②③④,共有4个.
故选:D.
①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D在AB的中垂线上;
④利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时,需要熟悉等腰三角形的判定与性质.
9.【答案】A
【解析】
解:①∵三角形ABC中,∠A的平分线交BC于点D,DE⊥AC,DF⊥AB,
∴∠ADE=∠ADF,DF=DE,
∴AF=AE,
∴∠AFE=∠AEF,故正确;
②∵DF=DE,AF=AE,
∴点D在EF的垂直平分线上,点A在EF的垂直平分线上,
∴AD垂直平分EF,故正确;
③∵S△BFD=BF?DF,S△CDE=CE?DE,DF=DE,
∴;故正确;
④∵∠EFD不一定等于∠BDF,
∴EF不一定平行BC.故错误.
故选A.
由三角形ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,根据角平分线的性质,可得DE=DF,∠ADE=∠ADF,又由角平分线的性质,可得AF=AE,继而证得①∠AFE=∠AEF;又由线段垂直平分线的判定,可得②AD垂直平分EF;然后利用三角形的面积公式求解即可得③.
此题考查了角平分线的性质、线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
10.【答案】A
【解析】
解:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC=S△ABD+S△ACD,
∴×4×2+×AC×2=7,
解得AC=3.
故选:A.
过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据S△ABC=S△ABD+S△ACD列出方程求解即可.
本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.
11.【答案】B
【解析】
解:∵∠ABC=50°,∠ACB=60°,
∴∠BAC=180°-∠ABC-∠ACB=180°-50°-60°=70°,
故A选项正确,
∵BD平分∠ABC,
∴∠ABO=∠ABC=×50°=25°,
在△ABO中,
∠AOB=180°-∠BAC-∠ABO=180°-70°-25°=85°,
∴∠DOC=∠AOB=85°,
故B选项错误;
∵CD平分∠ACE,
∴∠ACD=(180°-60°)=60°,
∴∠BDC=180°-85°-60°=35°,
故C选项正确;
∵BD、CD分别是∠ABC和∠ACE的平分线,
∴D到AB、AC、BC的距离相等,
∴AD是△ABC的外角平分线,
∴∠DAC=(180°-70°)=55°,
故D选项正确.
故选:B.
根据三角形的内角和定理列式计算即可求出∠BAC=70°,再根据角平分线的定义求出∠ABO,然后利用三角形的内角和定理求出∠AOB再根据对顶角相等可得∠DOC=∠AOB,根据邻补角的定义和角平分线的定义求出∠DCO,再利用三角形的内角和定理列式计算即可∠BDC,判断出AD为三角形的外角平分线,然后列式计算即可求出∠DAC.
本题考查了角平分线的性质,三角形的内角和定理,角平分线的定义,熟记定理和概念是解题的关键.
12.【答案】A
【解析】
解:∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∴BC边上的高=3×4÷5=,
∵AD平分∠BAC,
∴点D到AB、AC上的距离相等,设为h,
则S△ABC=×3h+×4h=×5×,
解得h=,
S△ABD=×3×=BD?,
解得BD=.
故选A.
根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到角的两边的距离相等可得点D到AB、AC上的距离相等,然后利用三角形的面积求出点D到AB的长,再利用△ABD的面积列式计算即可得解.
本题考查了角平分线的性质,三角形的面积,勾股定理,利用三角形的面积分别求出相应的高是解题的关键.
13.【答案】
【解析】
解:∵∠C=90°,∠A=30°,
∴∠ABC=180°-30°-90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=∠ABC=30°,
∴BC=AB=3,
∴CD=BC?tan30°=3×=,
∵BD是∠ABC的平分线,
又∵角平线上点到角两边距离相等,
∴点D到AB的距离=CD=,
故答案为:.
求出∠ABC,求出∠DBC,根据含30度角的直角三角形性质求出BC,CD,问题即可求出.
本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.
14.【答案】4:3
【解析】
解:∵AD是△ABC的角平分线,
∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2,
∴h1=h2,
∴△ABD与△ACD的面积之比=AB:AC=4:3,
故答案为4:3.
根据角平分线的性质,可得出△ABD的边AB上的高与△ACD的AC上的高相等,估计三角形的面积公式,即可得出△ABD与△ACD的面积之比等于对应边之比.
本题考查了角平分线的性质,以及三角形的面积公式,熟练掌握三角形角平分线的性质是解题的关键.
15.【答案】3
【解析】
解:作DE⊥AB于E,
∵AD是∠CAB的角平分线,∠C=90°,
∴DE=DC,
∵DC=3,
∴DE=3,
即点D到AB的距离DE=3.
故答案为:3.
根据角平分线上的点到角的两边的距离相等可得DE=DC即可得解.
本题主要考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.
16.【答案】3
【解析】
解:作PF⊥AD于D,如图,
∵四边形ABCD为菱形,
∴AC平分∠BAD,
∵PE⊥AB,PF⊥AD,
∴PF=PE=3,
即点P到AD的距离为3.
故答案为:3.
作PF⊥AD于D,如图,根据菱形的性质得AC平分∠BAD,然后根据角平分线的性质得PF=PE=3.
本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了菱形的性质.
17.【答案】15
【解析】
解:过D作DE⊥BC于E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴AD=DE=3,
∴△BDC的面积是×DE×BC=×10×3=15,
故答案为:15.
过D作DE⊥BC于E,根据角平分线性质求出DE=3,根据三角形的面积求出即可.
本题考查了角平分线性质和三角形的面积的应用,注意:角平分线上的点到角两边的距离相等.
18.【答案】3
【解析】
解:过点D作DE⊥BC于E,
∵在Rt△ABC中,∠A=90°,BD平分∠ABC,
即AD⊥BA,
∴DE=AD,
∵在Rt△ABC中,∠A=90°,AB=4,BD=5,
∴AD==3,
∴DE=AD=3,
∴点D到BC的距离是3.
故答案为:3.
首先过点D作DE⊥BC于E,由在Rt△ABC中,∠A=90°,BD平分∠ABC,根据角平分线的性质,即可得DE=AD,又由勾股定理求得AD的长,继而求得答案.
此题考查了角平分线的性质与勾股定理的应用.此题难度不大,注意数形结合思想的应用,注意掌握辅助线的作法.
19.【答案】15
【解析】
解:作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为×3×10=15.
故答案是:15.
要求△ABD的面积,现有AB=10可作为三角形的底,只需求出该底上的高即可,需作DE⊥AB于E.根据角平分线的性质求得DE的长,即可求解.
此题主要考查角平分线的性质;熟练运用角平分线的性质定理,是很重要的,作出并求出三角形AB边上的高时解答本题的关键.
20.【答案】35
【解析】
解:∵QC⊥OA于C,QD⊥OB于D,QC=QD,
∴OQ是∠AOB的平分线,
∵∠AOB=70°,
∴∠AOQ=∠A0B=×70°=35°.
故答案为:35.
根据到角的两边距离相等的点在角的平分线上判断OQ是∠AOB的平分线,然后根据角平分线的定义解答即可.
本题考查了角平分线的判定以及角平分线的定义,根据到角的两边距离相等的点在角的平分线上判断OQ是∠AOB的平分线是解题的关键.
21.【答案】3
【解析】
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AC=6,BC=8,
∴AB===10,
∵AD平分∠CAB,
∴CD=DE,
∴S△ABC=AC?CD+AB?DE=AC?BC,
即×6?CD+×10?CD=×6×8,
解得CD=3.
故答案为:3.
过点D作DE⊥AB于E,利用勾股定理列式求出AB,再根据角平分线上的点到角的两边距离相等可得CD=DE,然后根据△ABC的面积列式计算即可得解.
本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质并利用三角形的面积列出方程是解题的关键.
22.【答案】10
【解析】
解:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PE=PD=10.
故答案为:10.
根据角平分线上的点到角的两边距离相等可得PE=PD.
本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键,作出图形更形象直观.
23.【答案】4
【解析】
解:∵BD是∠ABC的平分线,PE⊥AB于点E,PE=4cm,
∴点P到BC的距离=PE=4cm.
故答案为4.
BD是∠ABC的平分线,再根据角平分线的性质即可得到点P到BC的距离.
本题考查了角平分线的性质.由已知能够注意到P到BC的距离即为PE长是解决的关键.
24.【答案】4
【解析】
解:∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DF=DE=2,
∴S△BCD=?BC×DF=×4×2=4
故答案为:4.
根据角平分线的性质定理可得DF=DE;最后根据三角形的面积=底×高÷2,求出△BCD的面积是多少即可.
此题主要考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:角的平分线上的点到角的两边的距离相等.
25.【答案】4
【解析】
解:∵在Rt△ACD中,∠C=90°,CD=2,AD=4,
∴∠CAD=30°,
∴由勾股定理得:AC==2,
∵AD平分∠BAC,
∴∠BAC=60°,
∴∠B=30°,
∴AB=2AC=4,
故答案为:4.
先求出∠CAD=30°,求出∠BAC=60°,∠B=30°,根据勾股定理求出AC,再求出AB=2AC,代入求出即可.
本题考查了含30度角的直角三角形性质,三角形内角和定理,勾股定理的应用,解此题的关键是求出AC长和求出∠B=30°,注意:在直角三角形中,如果有一个角等于30°,那么它所对的直角边等于斜边的一半.
第2页,共20页
第1页,共20页
