第13章 全等三角形单元考试题(有答案)
文档属性
| 名称 | 第13章 全等三角形单元考试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-25 00:00:00 | ||
图片预览



文档简介
华师大版数学八年级上册第13章全等三角形单元考试题
总分:150分,时间:120分钟;
姓名: ;时间: ;
选择题(4分×12=48分)
通过下列方式得到的图形与原图形不是全等三角形的是( )
平移 B.旋转 C.对称 D.放大
下列对全等四边形的说法,正确的是( )
由两对全等三角形组合成的四边形是全等四边形;
能够分割为两对全等三角形的四边形是全等四边形;
四条边对应相等,三个角对应相等的四边形是全等四边形;
沿对角线两旁的三角形对应全等的四边形是全等四边形;
3.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若a2=b2,则a=b.其中真命题的个数有( )
A.3个 B.2个 C.1个 D.0个
如图所示,AB、CD相交于点O,△AOC≌△BOD,点E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可能是( )
A.∠OCE=∠ODF B.∠CEA=∠DFB C.CE=DF D.OE=OF
5.尺规作图作∠AOB 的平分线的方法如下:以点 O 为圆心,任意长为半径画弧,交 OA,OB 于点 C,D,再分别以点 C,D 为圆心,大于 CD 长为半径画弧,两弧在∠AOB 的内部交于点 P,作射线 OP.由以上作法得△OCP≌△ODP 的根据是( )
A.SAS B.ASA C.AAS D.SSS
6.已知△ABC 的三边长分别为 3,4,5,△DEF 的三边长分别为 3,3x-2,2x+1, 若这两个三角形全等,则 x 的值为( )
A.2 B. 2或 C. 或 D. 2或或
7.如图所示,在△ABC中,AB=BD=AC,AD=CD,则∠ADB的度数是( )
A.72° B.60° C.45° D.36°
8.如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB B.与∠CBO互余的角有两个
C.∠AOB=90° D.点O是CD的中点
如图所示,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
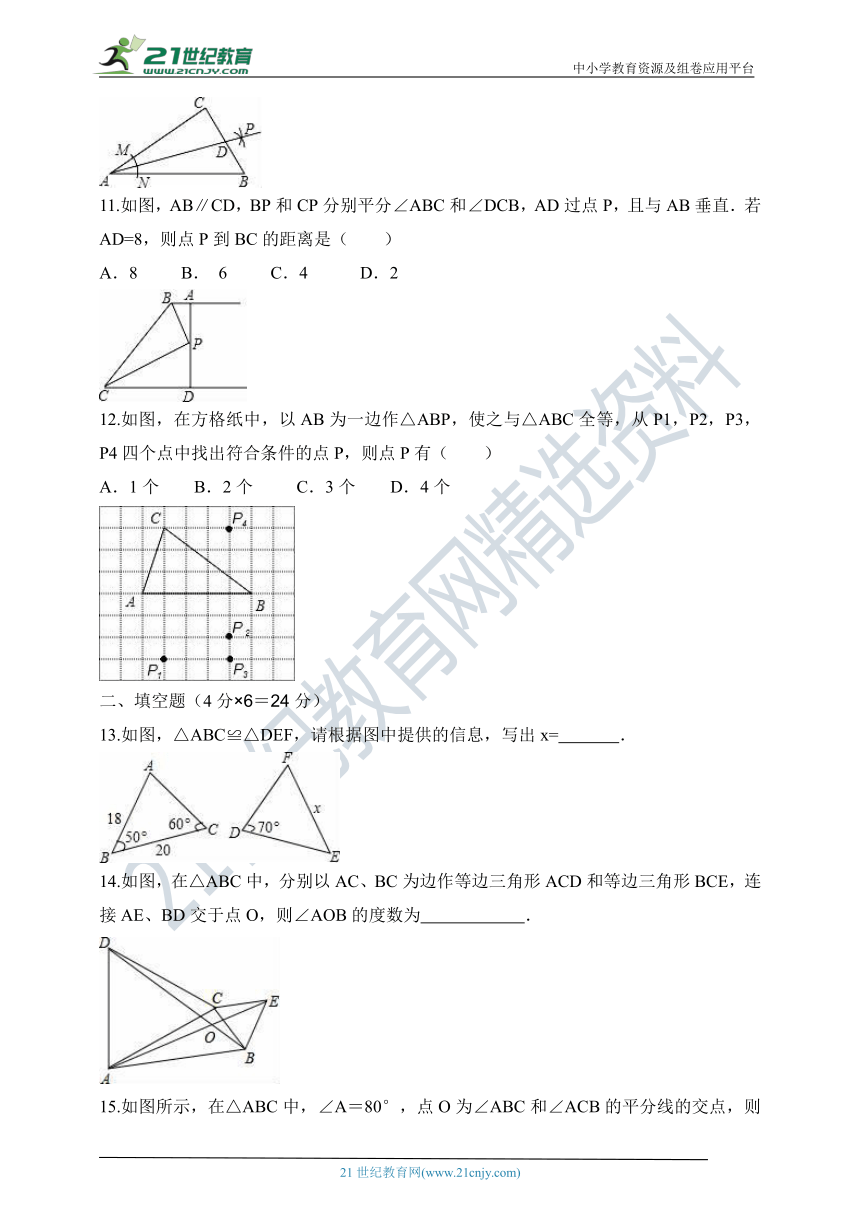
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B. 6 C.4 D.2
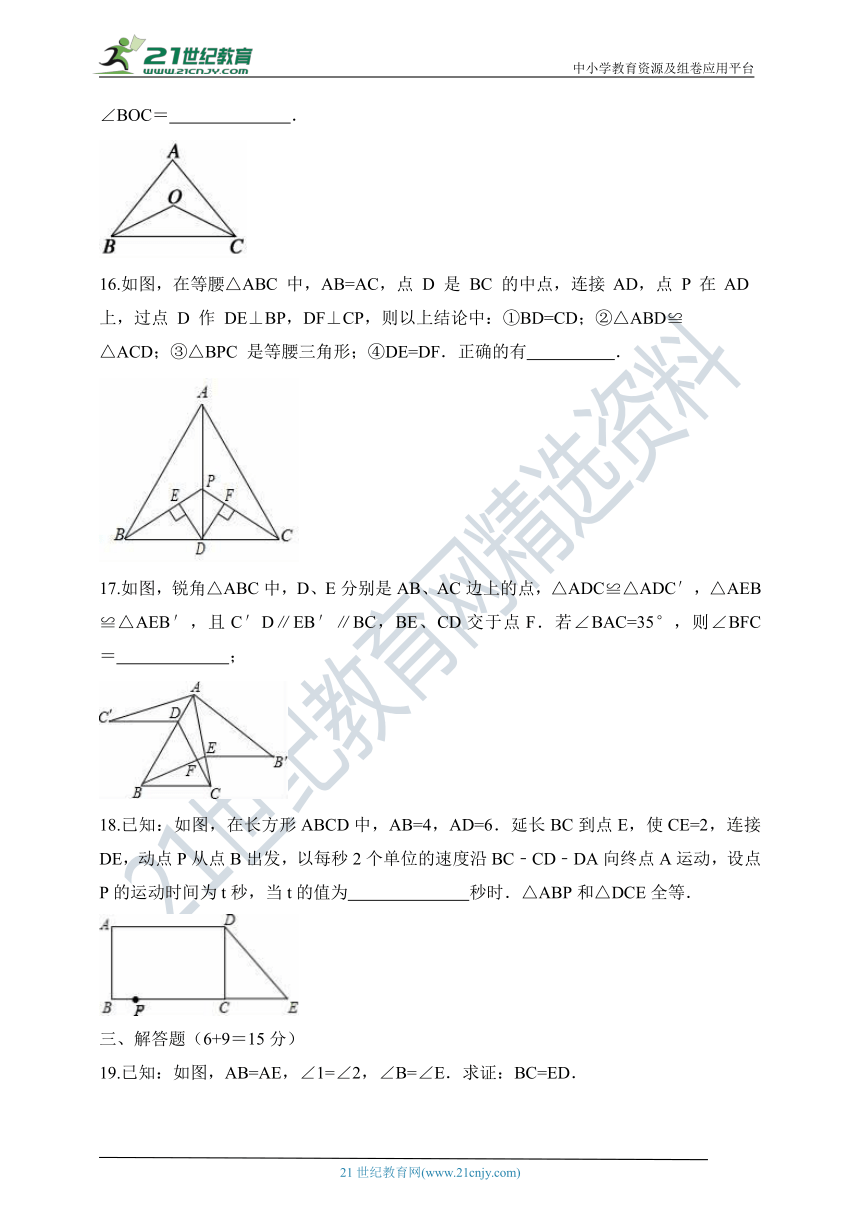
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
填空题(4分×6=24分)
如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
14.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为 .
如图所示,在△ABC中,∠A=80°,点O为∠ABC和∠ACB的平分线的交点,则∠BOC= .
16.如图,在等腰△ABC 中,AB=AC,点 D 是 BC 的中点,连接 AD,点 P 在 AD
上,过点 D 作 DE⊥BP,DF⊥CP,则以上结论中:①BD=CD;②△ABD≌
△ACD;③△BPC 是等腰三角形;④DE=DF.正确的有 .
如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC= ;
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为 秒时.△ABP和△DCE全等.
解答题(6+9=15分)
已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
20.如图所示,点B、C在∠SAF的两边上,且AB=AC.
(1)请按下列语句用尺规作出图形(不写作法,保留作图痕迹);
①AN⊥BC,垂足为点N;
②∠SBC的平分线交AN的延长线于点M;
③连结CM.
该图中有几对全等三角形?
解答题(8+11+11+11=41分)
如图所示,已知△ABC中,AB=AC,D、E分别是AB、BC上的点,连结DE并延长交AC的延长线于点F,若DE=EF,求证:DB=CF.
22.八(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
23.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点. ,且EF交正方形外角 的平行线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
24.(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图③,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连结BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
解答题(12分)
25.如图,已知ΔABC 中,AB=AC=10 厘米,BC=8 厘米,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,ΔBPD 与 CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使ΔBPD 与 CQP全等?
若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿ΔABC三边运动,求经过多长时间点P与点Q第一次在ΔABC的哪条边上相遇?
华师大版数学八年级上册第13章全等三角形单元考试题答案
选择题
DCBCD AABDB CC
填空题
13.20;
14.120°;
15.130°;
16.①②③④;
17.110°;
18.1或7;
解答题
证明略;
△ABN≌△ACN,△ABM≌△ACM,△BMN≌△CMN,共3对;
解答题
证明略;
解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件.
(2)方案(Ⅱ)可行.
证明:在△OPM和△OPN中
∴△OPM≌△OPN(SSS)
∴∠AOP=∠BOP(全等三角形对应角相等)
(3)当∠AOB是直角时,此方案可行.
∵四边形内角和为360°,又若PM⊥OA,PN⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°,
∴∠AOB=90°
∵若PM⊥OA,PN⊥OB,
且PM=PN
∴OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上)
(1)证明略;(2)成立,证明略;(3)成立,证明略;
24.解:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中,∵∠ABD=∠CAE,∠BDA=∠CEA,AB=AC,∴△ADB≌△CEA(A.A.S.),
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.
(2)成立.证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α.
∴∠CAE=∠ABD.
在△ADB和△CEA中,∵∠ABD=∠CAE,∠BDA=∠CEA,AB=AC,∴△ADB≌△CEA(A.A.S.).
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE.
∵BF=AF.
在△DBF和△EAF中,
∵FB=FA,∠FBD=∠FAE,BD=AE,∴△DBF≌△EAF,
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
解答题
25. ⑴①全等。
理由:∵AB=AC,∴∠B=∠C,运动1秒时BP=3,CP=5,CQ=3
∵D为AB中点,AB=10,∴BD=5.
∴BP=CQ,BD=CP,∴△BPD≌△CQP
②若Q与P的运动速度不等,则BP≠CQ,若△BPD与△CQP全等,则BP=CP=4
CQ=5,Q的运动速度为5× cm/s
⑵设经过t秒两点第一次相遇则
( -3)t=20
t=
3t=80,
80÷28=2
×28=24,所以在AB边上。
即经过 两点第一次相遇,相遇点在AB上。
总分:150分,时间:120分钟;
姓名: ;时间: ;
选择题(4分×12=48分)
通过下列方式得到的图形与原图形不是全等三角形的是( )
平移 B.旋转 C.对称 D.放大
下列对全等四边形的说法,正确的是( )
由两对全等三角形组合成的四边形是全等四边形;
能够分割为两对全等三角形的四边形是全等四边形;
四条边对应相等,三个角对应相等的四边形是全等四边形;
沿对角线两旁的三角形对应全等的四边形是全等四边形;
3.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若a2=b2,则a=b.其中真命题的个数有( )
A.3个 B.2个 C.1个 D.0个
如图所示,AB、CD相交于点O,△AOC≌△BOD,点E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可能是( )
A.∠OCE=∠ODF B.∠CEA=∠DFB C.CE=DF D.OE=OF
5.尺规作图作∠AOB 的平分线的方法如下:以点 O 为圆心,任意长为半径画弧,交 OA,OB 于点 C,D,再分别以点 C,D 为圆心,大于 CD 长为半径画弧,两弧在∠AOB 的内部交于点 P,作射线 OP.由以上作法得△OCP≌△ODP 的根据是( )
A.SAS B.ASA C.AAS D.SSS
6.已知△ABC 的三边长分别为 3,4,5,△DEF 的三边长分别为 3,3x-2,2x+1, 若这两个三角形全等,则 x 的值为( )
A.2 B. 2或 C. 或 D. 2或或
7.如图所示,在△ABC中,AB=BD=AC,AD=CD,则∠ADB的度数是( )
A.72° B.60° C.45° D.36°
8.如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB B.与∠CBO互余的角有两个
C.∠AOB=90° D.点O是CD的中点
如图所示,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B. 6 C.4 D.2
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
填空题(4分×6=24分)
如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
14.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为 .
如图所示,在△ABC中,∠A=80°,点O为∠ABC和∠ACB的平分线的交点,则∠BOC= .
16.如图,在等腰△ABC 中,AB=AC,点 D 是 BC 的中点,连接 AD,点 P 在 AD
上,过点 D 作 DE⊥BP,DF⊥CP,则以上结论中:①BD=CD;②△ABD≌
△ACD;③△BPC 是等腰三角形;④DE=DF.正确的有 .
如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC= ;
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为 秒时.△ABP和△DCE全等.
解答题(6+9=15分)
已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
20.如图所示,点B、C在∠SAF的两边上,且AB=AC.
(1)请按下列语句用尺规作出图形(不写作法,保留作图痕迹);
①AN⊥BC,垂足为点N;
②∠SBC的平分线交AN的延长线于点M;
③连结CM.
该图中有几对全等三角形?
解答题(8+11+11+11=41分)
如图所示,已知△ABC中,AB=AC,D、E分别是AB、BC上的点,连结DE并延长交AC的延长线于点F,若DE=EF,求证:DB=CF.
22.八(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.
23.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点. ,且EF交正方形外角 的平行线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
24.(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由;
(3)拓展与应用:如图③,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连结BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
解答题(12分)
25.如图,已知ΔABC 中,AB=AC=10 厘米,BC=8 厘米,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,ΔBPD 与 CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使ΔBPD 与 CQP全等?
若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿ΔABC三边运动,求经过多长时间点P与点Q第一次在ΔABC的哪条边上相遇?
华师大版数学八年级上册第13章全等三角形单元考试题答案
选择题
DCBCD AABDB CC
填空题
13.20;
14.120°;
15.130°;
16.①②③④;
17.110°;
18.1或7;
解答题
证明略;
△ABN≌△ACN,△ABM≌△ACM,△BMN≌△CMN,共3对;
解答题
证明略;
解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件.
(2)方案(Ⅱ)可行.
证明:在△OPM和△OPN中
∴△OPM≌△OPN(SSS)
∴∠AOP=∠BOP(全等三角形对应角相等)
(3)当∠AOB是直角时,此方案可行.
∵四边形内角和为360°,又若PM⊥OA,PN⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°,
∴∠AOB=90°
∵若PM⊥OA,PN⊥OB,
且PM=PN
∴OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上)
(1)证明略;(2)成立,证明略;(3)成立,证明略;
24.解:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中,∵∠ABD=∠CAE,∠BDA=∠CEA,AB=AC,∴△ADB≌△CEA(A.A.S.),
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.
(2)成立.证明:∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α.
∴∠CAE=∠ABD.
在△ADB和△CEA中,∵∠ABD=∠CAE,∠BDA=∠CEA,AB=AC,∴△ADB≌△CEA(A.A.S.).
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE.
∵BF=AF.
在△DBF和△EAF中,
∵FB=FA,∠FBD=∠FAE,BD=AE,∴△DBF≌△EAF,
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
解答题
25. ⑴①全等。
理由:∵AB=AC,∴∠B=∠C,运动1秒时BP=3,CP=5,CQ=3
∵D为AB中点,AB=10,∴BD=5.
∴BP=CQ,BD=CP,∴△BPD≌△CQP
②若Q与P的运动速度不等,则BP≠CQ,若△BPD与△CQP全等,则BP=CP=4
CQ=5,Q的运动速度为5× cm/s
⑵设经过t秒两点第一次相遇则
( -3)t=20
t=
3t=80,
80÷28=2
×28=24,所以在AB边上。
即经过 两点第一次相遇,相遇点在AB上。
