物理:第三章第五节《牛顿运动定律的应用》课件ppt(教科版必修1)(共23张ppt)
文档属性
| 名称 | 物理:第三章第五节《牛顿运动定律的应用》课件ppt(教科版必修1)(共23张ppt) |

|
|
| 格式 | rar | ||
| 文件大小 | 400.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-02-17 00:00:00 | ||
图片预览






文档简介
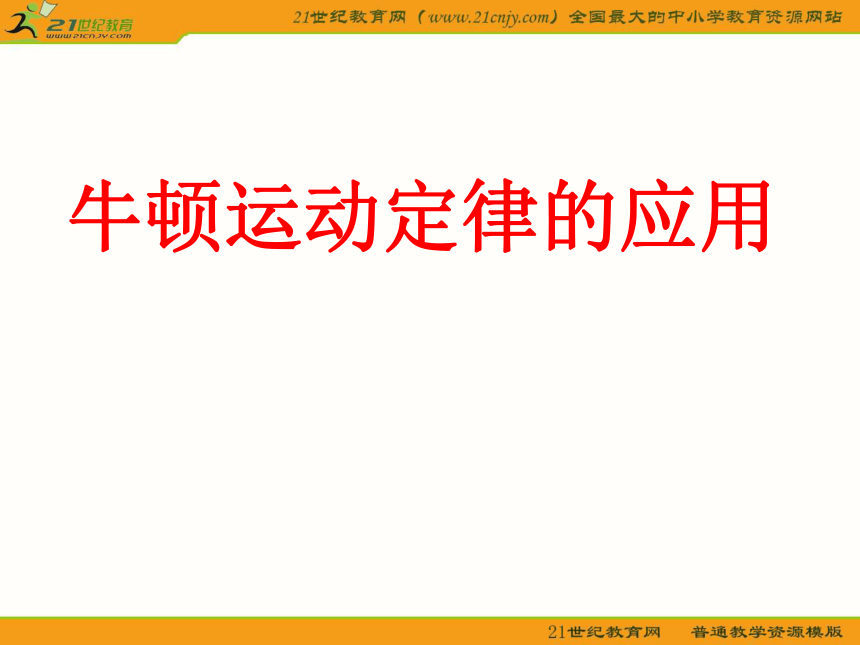
课件23张PPT。物理:第三章第五节《牛顿运动定律的应用》课件ppt(教科版必修1)牛顿运动定律的应用
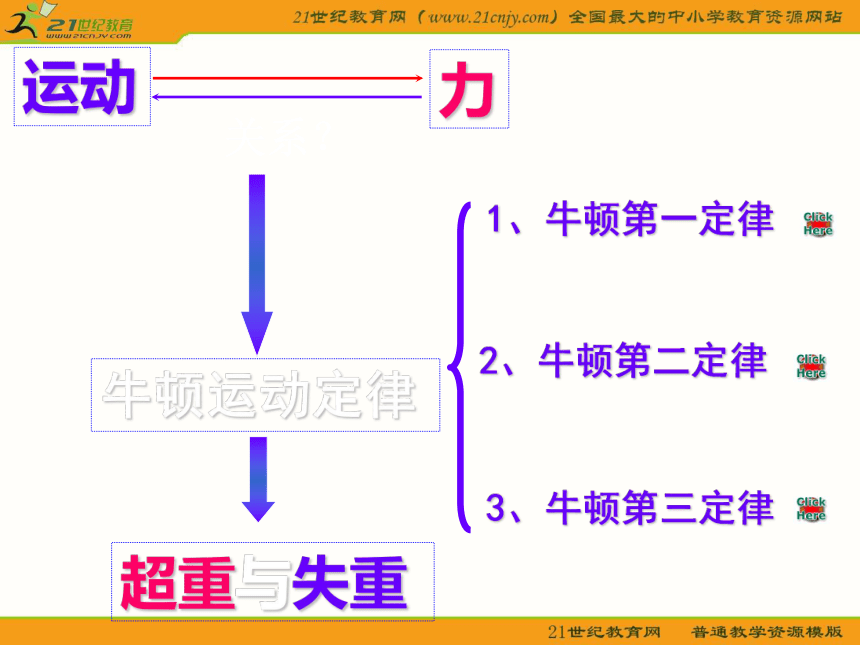
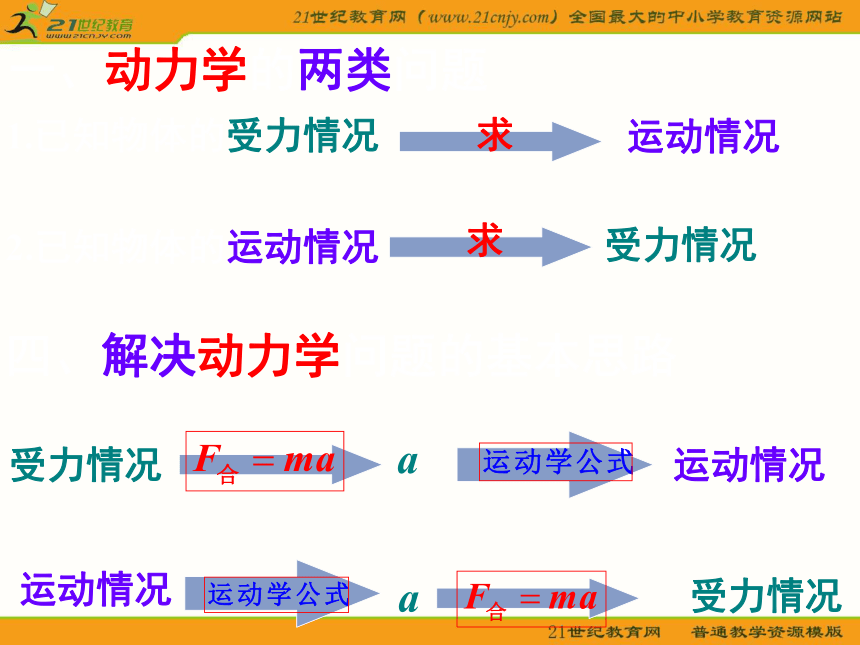
运动力牛顿运动定律1、牛顿第一定律2、牛顿第二定律3、牛顿第三定律超重与失重一、动力学的两类问题1.已知物体的受力情况运动情况2.已知物体的运动情况受力情况四、解决动力学问题的基本思路受力情况a运动情况运动情况a受力情况二、解题步骤:1.选取研究对象(哪个物体或哪几个物体组成的系统)2.受力分析,画出受力的示意图3.建立坐标系,选择运动方向或加速度方向为正方向4.根据牛顿定律、运动公式列出方程5.解方程,对结果进行分析、检验或讨论三、几种典型的解题方法:1.正交分解法2.整体法和隔离法3.假设法4.极限法5.图象法四、典型例题例1.(2005年广东卷1)一汽车在路面情况相同的公路上行驶,下面关于车速、惯性、质量和滑行路程的讨论,正确的是 ( )
A. 车速越大,它的惯性越大
B. 质量越大,它的惯性越大
C. 车速越大,刹车后滑行的路程越长
D. 车速越大,刹车后滑行的路程越长,所以惯性越大B C 例2.下列关于运动状态与受力关系的说法中,正确的是: ( )
A.物体的运动状态发生变化,物体的受力情况一定变化
B.物体在恒力作用下,一定作匀变速直线运动
C.物体的运动状态保持不变,说明物体所受的合外力为零
D.物体作曲线运动时,受到的合外力可能是恒力C D例3. 如图所示, 位于光滑固定斜面上的小物体P受到一水平向右的推力的作用. 已知物块P沿斜面加速下滑. 现保持F的方向不变, 使其减小, 则加速度 ( )
A.一定变小 B.一定变大 C.一定不变
D.可能变小, 可能变大, 也可能不变解: 画出物体P受力图如图示:由牛顿第二定律得mgsinθ-Fcosθ=ma保持F的方向不变,使F减小,
则加速度a一定变大B例4 .一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a,如图所示.在物体始终相对于斜面静止的条件下,下列说法中正确的是 ( )A.当θ 一定时,a 越大,斜面对物体的正压力越小
B.当θ 一定时,a 越大,斜面对物体的摩擦力越大
C.当a 一定时, θ 越大,斜面对物体的正压力越小
D.当a 一定时, θ 越大,斜面对物体的摩擦力越小?解:物体受力情况如图所示,由牛顿第二定律得,f - mgsin θ = masin θ
FN - mgcos θ = macos θ ∴ f = m(g+a) sin θ
FN = m(g+a) cos θ 若不将加速度分解, 则要解二元一次方程组.B C例5物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时 ( )
A.A受到B的摩擦力沿斜面方向向上
B.A受到B的摩擦力沿斜面方向向下
C.A、B之间的摩擦力为零
D.A、B之间是否存在摩擦力取决于A、B表面的性质解:对A、B整体,
由牛顿第二定律得,例5.物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时 ( )
A.A受到B的摩擦力沿斜面方向向上
B.A受到B的摩擦力沿斜面方向向下
C.A、B之间的摩擦力为零
D.A、B之间是否存在摩擦力取决于A、B表面的性质C解:对A、B整体,由牛顿第二定律得,假设B受摩擦力如图所示,则对B,由牛顿第二定律得,例6. 如图所示,一根轻质弹簧和一根细线共同拉住一个质量为m的小球,平衡时细线恰是水平的,弹簧与竖直方向的夹角为θ.若突然剪断细线,则在刚剪断的瞬时,弹簧拉力的大小是 ,小球加速度的大小为 ,方向与竖直方向的夹角等于 . 小球再回到原处时弹簧拉力的大小是 .解:小球受力如图示,由平衡条件得 弹簧拉力为 F= mg/cosθ剪断线的瞬时,弹簧拉力不变仍为F.小球加速度的大小为a=T/m=g tanθ
方向沿水平方向.小球再次回到原处时,由圆周运动规律得F1 -mg cosθ=mv2 / l =0∴F1 = mg cosθmg/cosθg tanθ90°mg cosθ例7.在运动的升降机中天花板上用细线悬挂一个物体A,下面吊着一个轻质弹簧秤(弹簧秤的质量不计),弹簧秤下吊着物体B,如下图所示,物体A和B的质量相等,都为m=5kg,某一时刻弹簧秤的读数为40N,设g=10 m/s2,则细线的拉力等于_____ ,若将细线剪断,在剪断细线瞬间物体A的加速度是 ,方向 ______ ;
物体B的加速度是 ;
方向 _____ . 80N18 m/s2向下2 m/s2向下例8.如图,有一斜木块,斜面是光滑的,倾角为θ,放在水平面上,用竖直放置的固定挡板A与斜面夹住一个光滑球,球质量为m,要使球对竖直挡板无压力,球连同斜木块一起应向 (填左、右)做加速运动,加速度大小是 . 解: 画出小球的受力图如图示: 合力一定沿水平方向向左,F=mgtan θ∴a= gtan θ左gtanθ 例9. 一质量为M、倾角为θ的楔形木块,静止在水平桌面上,与桌面的动摩擦因素为μ,一物块质量为m,置于楔形木块的斜面上,物块与斜面的接触是光滑的,为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图示,此水平力的大小等于 .解:对于物块,受力如图示:物块相对斜面静止,只能有向左的加速度,
所以合力一定向左.由牛顿运动定律得mg tan θ=ma a= gtan θ对于整体受力如图示:由牛顿运动定律得F – f = (m+M)aFN2 -(m+M)g=0f= μFN2= μ (m+M)g ∴F=f+(m+M)a= (m+M)g(μ +tan θ) (m+M)g(μ+ tanθ)解:由牛顿第二定律得, D 电梯对人的支持力为由牛顿第三定律 得,所求压力 为FN′=4mg/3 ,FN=ma+mg=4mg/3 ,FN-mg=ma ,例11. (2005年北京春季理综20)如图,一个盛水的容器底部有一小孔.静止时用手指堵住小孔不让它漏水,假设容器在下述几种运动过程中始终保持平动,且忽略空气阻力,则( )
A.容器自由下落时,小孔向下漏水
B.将容器竖直向上抛出,容器向上运动时,小孔向下漏水;容器向下运动时,小孔不向下漏水
C.将容器水平抛出,容器在运动中小孔向下漏水
D.将容器斜向上抛出,容器在运动中小孔不向下漏水D容器及水均处于完全失重状态,水不产生压强,小孔的上下方压强相等,所以水不会流出.例l2. (2005年陕西、四川、云南 1)如图所示,一物块位于光滑水平桌面上,用一大小为F 、方向如图所示的力去推它,使它以加速度a右运动。若保持力的方向不变而增大力的大小,则
A . a 变大 B . a不变 C.a变小 D . 因为物块的质量未知,故不能确定a变化的趋势例l2.(2005年陕西、四川、云南 1)如图所示,一物块位于光滑水平桌面上,用一大小为F 、方向如图所示的力去推它,使它以加速度a右运动.若保持力的方向不变而增大力的大小,则 ( )
A . a 变大 B . a不变 C.a变小 D . 因为物块的质量未知,故不能确定a变化的趋势αFcosα=ma,解:根据牛顿第二定律得,A 例13.人和雪橇的总质量为75kg,沿倾角θ=37°且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为
(4, 15),CD是曲线AD的渐近线,g取10m/s2,
试回答和求解:
⑴雪橇在下滑过程中,开始做什么
运动,最后做什么运动?
⑵当雪橇的速度为5m/s时,雪橇
的加速度为多大?
⑶雪橇与斜坡间的动摩擦因数μ多大?解: ⑴ 由图线可知,雪橇开始以5m/s的初速度作加速度逐渐减小的变加速运动,最后以10m/s作匀速运动⑵ t=0,v0= 5m/s 时AB的斜率等于加速度的大小a=Δv/Δt= 10/4 = 2.5 m/s2⑶ t=0 , v0= 5m/s , f0=kv0 由牛顿运动定律 mgsinθ - μ mgcosθ –kv0 = ma ①t=4s vt= 10m/s ft=kvt mgsinθ - μ mgcosθ –kvt =0 ② 解① ②得 k=37. 5 Ns/mμ= 0.125
运动力牛顿运动定律1、牛顿第一定律2、牛顿第二定律3、牛顿第三定律超重与失重一、动力学的两类问题1.已知物体的受力情况运动情况2.已知物体的运动情况受力情况四、解决动力学问题的基本思路受力情况a运动情况运动情况a受力情况二、解题步骤:1.选取研究对象(哪个物体或哪几个物体组成的系统)2.受力分析,画出受力的示意图3.建立坐标系,选择运动方向或加速度方向为正方向4.根据牛顿定律、运动公式列出方程5.解方程,对结果进行分析、检验或讨论三、几种典型的解题方法:1.正交分解法2.整体法和隔离法3.假设法4.极限法5.图象法四、典型例题例1.(2005年广东卷1)一汽车在路面情况相同的公路上行驶,下面关于车速、惯性、质量和滑行路程的讨论,正确的是 ( )
A. 车速越大,它的惯性越大
B. 质量越大,它的惯性越大
C. 车速越大,刹车后滑行的路程越长
D. 车速越大,刹车后滑行的路程越长,所以惯性越大B C 例2.下列关于运动状态与受力关系的说法中,正确的是: ( )
A.物体的运动状态发生变化,物体的受力情况一定变化
B.物体在恒力作用下,一定作匀变速直线运动
C.物体的运动状态保持不变,说明物体所受的合外力为零
D.物体作曲线运动时,受到的合外力可能是恒力C D例3. 如图所示, 位于光滑固定斜面上的小物体P受到一水平向右的推力的作用. 已知物块P沿斜面加速下滑. 现保持F的方向不变, 使其减小, 则加速度 ( )
A.一定变小 B.一定变大 C.一定不变
D.可能变小, 可能变大, 也可能不变解: 画出物体P受力图如图示:由牛顿第二定律得mgsinθ-Fcosθ=ma保持F的方向不变,使F减小,
则加速度a一定变大B例4 .一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a,如图所示.在物体始终相对于斜面静止的条件下,下列说法中正确的是 ( )A.当θ 一定时,a 越大,斜面对物体的正压力越小
B.当θ 一定时,a 越大,斜面对物体的摩擦力越大
C.当a 一定时, θ 越大,斜面对物体的正压力越小
D.当a 一定时, θ 越大,斜面对物体的摩擦力越小?解:物体受力情况如图所示,由牛顿第二定律得,f - mgsin θ = masin θ
FN - mgcos θ = macos θ ∴ f = m(g+a) sin θ
FN = m(g+a) cos θ 若不将加速度分解, 则要解二元一次方程组.B C例5物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时 ( )
A.A受到B的摩擦力沿斜面方向向上
B.A受到B的摩擦力沿斜面方向向下
C.A、B之间的摩擦力为零
D.A、B之间是否存在摩擦力取决于A、B表面的性质解:对A、B整体,
由牛顿第二定律得,例5.物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时 ( )
A.A受到B的摩擦力沿斜面方向向上
B.A受到B的摩擦力沿斜面方向向下
C.A、B之间的摩擦力为零
D.A、B之间是否存在摩擦力取决于A、B表面的性质C解:对A、B整体,由牛顿第二定律得,假设B受摩擦力如图所示,则对B,由牛顿第二定律得,例6. 如图所示,一根轻质弹簧和一根细线共同拉住一个质量为m的小球,平衡时细线恰是水平的,弹簧与竖直方向的夹角为θ.若突然剪断细线,则在刚剪断的瞬时,弹簧拉力的大小是 ,小球加速度的大小为 ,方向与竖直方向的夹角等于 . 小球再回到原处时弹簧拉力的大小是 .解:小球受力如图示,由平衡条件得 弹簧拉力为 F= mg/cosθ剪断线的瞬时,弹簧拉力不变仍为F.小球加速度的大小为a=T/m=g tanθ
方向沿水平方向.小球再次回到原处时,由圆周运动规律得F1 -mg cosθ=mv2 / l =0∴F1 = mg cosθmg/cosθg tanθ90°mg cosθ例7.在运动的升降机中天花板上用细线悬挂一个物体A,下面吊着一个轻质弹簧秤(弹簧秤的质量不计),弹簧秤下吊着物体B,如下图所示,物体A和B的质量相等,都为m=5kg,某一时刻弹簧秤的读数为40N,设g=10 m/s2,则细线的拉力等于_____ ,若将细线剪断,在剪断细线瞬间物体A的加速度是 ,方向 ______ ;
物体B的加速度是 ;
方向 _____ . 80N18 m/s2向下2 m/s2向下例8.如图,有一斜木块,斜面是光滑的,倾角为θ,放在水平面上,用竖直放置的固定挡板A与斜面夹住一个光滑球,球质量为m,要使球对竖直挡板无压力,球连同斜木块一起应向 (填左、右)做加速运动,加速度大小是 . 解: 画出小球的受力图如图示: 合力一定沿水平方向向左,F=mgtan θ∴a= gtan θ左gtanθ 例9. 一质量为M、倾角为θ的楔形木块,静止在水平桌面上,与桌面的动摩擦因素为μ,一物块质量为m,置于楔形木块的斜面上,物块与斜面的接触是光滑的,为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图示,此水平力的大小等于 .解:对于物块,受力如图示:物块相对斜面静止,只能有向左的加速度,
所以合力一定向左.由牛顿运动定律得mg tan θ=ma a= gtan θ对于整体受力如图示:由牛顿运动定律得F – f = (m+M)aFN2 -(m+M)g=0f= μFN2= μ (m+M)g ∴F=f+(m+M)a= (m+M)g(μ +tan θ) (m+M)g(μ+ tanθ)解:由牛顿第二定律得, D 电梯对人的支持力为由牛顿第三定律 得,所求压力 为FN′=4mg/3 ,FN=ma+mg=4mg/3 ,FN-mg=ma ,例11. (2005年北京春季理综20)如图,一个盛水的容器底部有一小孔.静止时用手指堵住小孔不让它漏水,假设容器在下述几种运动过程中始终保持平动,且忽略空气阻力,则( )
A.容器自由下落时,小孔向下漏水
B.将容器竖直向上抛出,容器向上运动时,小孔向下漏水;容器向下运动时,小孔不向下漏水
C.将容器水平抛出,容器在运动中小孔向下漏水
D.将容器斜向上抛出,容器在运动中小孔不向下漏水D容器及水均处于完全失重状态,水不产生压强,小孔的上下方压强相等,所以水不会流出.例l2. (2005年陕西、四川、云南 1)如图所示,一物块位于光滑水平桌面上,用一大小为F 、方向如图所示的力去推它,使它以加速度a右运动。若保持力的方向不变而增大力的大小,则
A . a 变大 B . a不变 C.a变小 D . 因为物块的质量未知,故不能确定a变化的趋势例l2.(2005年陕西、四川、云南 1)如图所示,一物块位于光滑水平桌面上,用一大小为F 、方向如图所示的力去推它,使它以加速度a右运动.若保持力的方向不变而增大力的大小,则 ( )
A . a 变大 B . a不变 C.a变小 D . 因为物块的质量未知,故不能确定a变化的趋势αFcosα=ma,解:根据牛顿第二定律得,A 例13.人和雪橇的总质量为75kg,沿倾角θ=37°且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为
(4, 15),CD是曲线AD的渐近线,g取10m/s2,
试回答和求解:
⑴雪橇在下滑过程中,开始做什么
运动,最后做什么运动?
⑵当雪橇的速度为5m/s时,雪橇
的加速度为多大?
⑶雪橇与斜坡间的动摩擦因数μ多大?解: ⑴ 由图线可知,雪橇开始以5m/s的初速度作加速度逐渐减小的变加速运动,最后以10m/s作匀速运动⑵ t=0,v0= 5m/s 时AB的斜率等于加速度的大小a=Δv/Δt= 10/4 = 2.5 m/s2⑶ t=0 , v0= 5m/s , f0=kv0 由牛顿运动定律 mgsinθ - μ mgcosθ –kv0 = ma ①t=4s vt= 10m/s ft=kvt mgsinθ - μ mgcosθ –kvt =0 ② 解① ②得 k=37. 5 Ns/mμ= 0.125
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
