14.3.2 因式分解--完全平方公式课件(共29张PPT)
文档属性
| 名称 | 14.3.2 因式分解--完全平方公式课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-29 00:00:00 | ||
图片预览








文档简介
课件29张PPT。14.3.2完全平方公式 14.3 因式分解 提取公因式法:ma+mb+mc=m(a+b+c)
运用公式法: ① a2-b2=(a+b)(a-b)
把下列各式分解因式① ② x4-16解:原式=ax2(x2-1)
=ax2(x+1)(x-1) =(x2+4)(x2-4)1、什么是分解因式?分解因式学了哪些方法?(有公因式,先提公因式。)(因式分解要彻底。)解:原式=(x2)2-42 =(x2 +4)(x+2)(x-2)课前复习:课前复习:2.除了平方差公式外,还学过了哪些公式? 完全平方公式完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
简记口诀:
首平方,尾平方,首尾积的2倍在中央。二、完全平方式 下列整式乘法运算你会吗?⑴、(n+m)2 = ——————;
⑵、(x-y)2 =——————;
⑶、(x+b)2 = ——————。以上的运算可直接用乘法公式:______________________。我们把完全平方公式反过来,得(a±b)2 =a2±2ab+b2 n2+2mn+ m2x2-2xy+y2 X2+2bx+b2 a2±2ab+b2 = (a±b)2 a 、b可以为单项式或多项式你从完全平方公式逆运算可发现什么?利用完全平方公式可对相关的多项式进行分解因式现在我们把这个公式反过来 很显然,我们可以运用以上这个公式来分解因式,这种分解因式的方法称为“完全平方公式法”用公式法正确分解因式关键是什么?熟知公式特征!完全平方式从项数看:完全平方式都是有 项3从每一项看:都有两项可化为两个数(或整式)的平方,
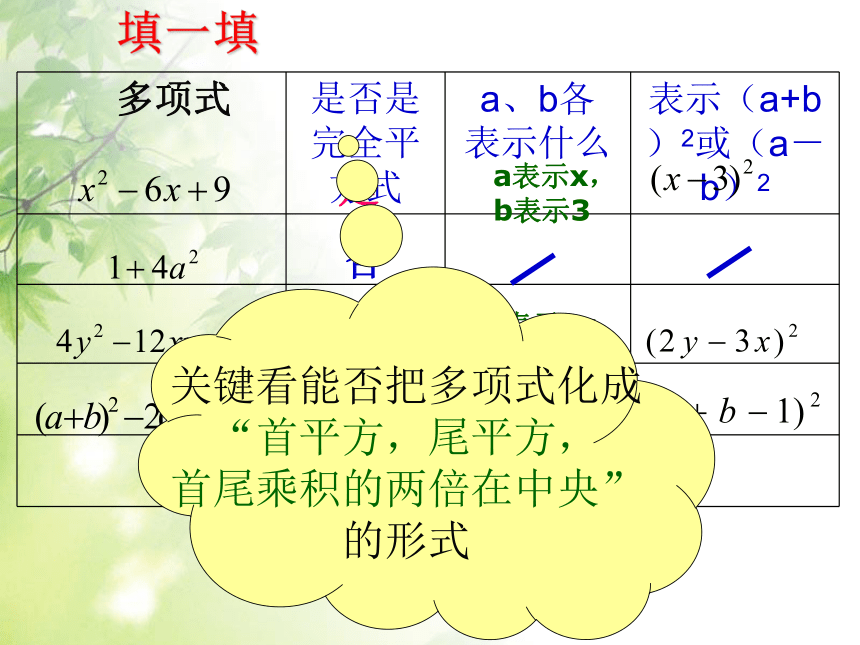
另一项为这两个数(或整式)的乘积的2倍.从符号看:带平方的项符号相同(同“+”或同“-”)a2 ± 2 a b + b2 = ( a ± b )2 否是a表示2y,
b表示3x是a表示(a+b),
b表示1填一填多项式是a表示x,
b表示3关键看能否把多项式化成
“首平方,尾平方,
首尾乘积的两倍在中央”
的形式1、回答:下列各式是不是完全平方式是是是否是否2.填写下表是是不是是不是不是a表示:x
b表示:3
a表示:2y
b表示:1
a表示:2x+y
b表示:3
3、请补上一项,使下列多项式成为完全平方式解:例题 分解因式的方法选择完全平式的特征
“方首平方,尾平方
首尾乘积的
两倍在中央”特征:
1、项数
2、有无公因式可提
3、是否符合公式法要求解:(3)3ax2+6axy+3ay2 解:(4)解:例题 -x2-4y2+4xy 分析:
1、项数
2、有无
公因式可提
3、是否符合
公式法要求
4、各项符号
特征
例6: 分解因式: (1) 3ax2+6axy+3ay2;
(2) (a+b)2-12(a+b)+36.分析:在(1)中有公因式3a,应先提出公因式,再进一步分解。
解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.三、新知识或新方法运用判断因式分解正误。(1) -x2-2xy-y2= -(x-y)2分析:首项(平方项)为负,首先提取“-”号 (2)a2+2ab-b2= (a-b)2分析:完全平方式 平方项符号相同(同正) 1:如何用符号表示完全平方公式?a2+2ab+b2=(a+b)2,
a2-2ab+b2=(a-b)2.2:完全平方公式的结构特点是什么?四、小结完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
简记口诀: 首平方,尾平方,首尾积的2倍在中央。因式分解:(1)25x2+10x+1 解:原式=(5x)2+2×5x×1+12练一练=(5x+1)2 (2)-a2-10a -25解:原式=-(a2+2×a×5+52)因式分解:(3)-a3b3+2a2b3-ab3解:原式=-ab3(a2-2a×1+12)
=-ab3(a-1)2练一练 (4)9 - 12(a-b) + 4 (a-b)2解:原式=32-2×3×2(a-b)+
=
=(3-2a+2b)2练习题:2、下列各式中,能用完全平方公式分解的是( )
A、a2+b2+ab B、a2+2ab-b2
C、a2-ab+2b2 D、-2ab+a2+b2
3、下列各式中,不能用完全平方公式分解的是( )
A、x2+y2-2xy B、x2+4xy+4y2
C、a2-ab+b2 D、-2ab+a2+b2
DC4、下列各式中,能用完全平方公式分解的是( )
A、x2+2xy-y2 B、x2-xy+y2
C、 D、
5、下列各式中,不能用完全平方公式分解的是( )
A、x4+6x2y2+9y4 B、x2n-2xnyn+y2n
C、x6-4x3y3+4y6 D、x4+x2y2+y4
DD6、把 分解因式得
( )
A、 B、
7、把 分解因式得
( )
A、 B、BA8、如果100x2+kxy+y2可以分解为(10x-y)2,那么k的值是( )
A、20 B、-20
C、10 D、-10
9、如果x2+mxy+9y2是一个完全平方式,那么m的值为( )
A、6 B、±6
C、3 D、±3 BB10、把 分解因式得( )
A、 B、
C、 D、
11、计算 的结果是( )
A、 1 B、-1
C、 2 D、-2CA12、请用公式法分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
13、请选择适当的方法分解因式:
(1) ax2+2a2x+a3; (2) -3x2+6xy-3y2.1.已知x2+4x+y2-2y+5=0,求 x-y 的值。解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1=能力提升把下列各式因式分解巩固练习挑战极限:
1、多项式:
(x+y)2-2(x2-y2)+(x-y)2能用完全平方公式分解吗?
2、在括号内补上一项,使多项式成为完全平方式:
X4+4x2+( )=( )2 数学书P :119练习1、2 《导学案》:103--104面练习四、作业再见
运用公式法: ① a2-b2=(a+b)(a-b)
把下列各式分解因式① ② x4-16解:原式=ax2(x2-1)
=ax2(x+1)(x-1) =(x2+4)(x2-4)1、什么是分解因式?分解因式学了哪些方法?(有公因式,先提公因式。)(因式分解要彻底。)解:原式=(x2)2-42 =(x2 +4)(x+2)(x-2)课前复习:课前复习:2.除了平方差公式外,还学过了哪些公式? 完全平方公式完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
简记口诀:
首平方,尾平方,首尾积的2倍在中央。二、完全平方式 下列整式乘法运算你会吗?⑴、(n+m)2 = ——————;
⑵、(x-y)2 =——————;
⑶、(x+b)2 = ——————。以上的运算可直接用乘法公式:______________________。我们把完全平方公式反过来,得(a±b)2 =a2±2ab+b2 n2+2mn+ m2x2-2xy+y2 X2+2bx+b2 a2±2ab+b2 = (a±b)2 a 、b可以为单项式或多项式你从完全平方公式逆运算可发现什么?利用完全平方公式可对相关的多项式进行分解因式现在我们把这个公式反过来 很显然,我们可以运用以上这个公式来分解因式,这种分解因式的方法称为“完全平方公式法”用公式法正确分解因式关键是什么?熟知公式特征!完全平方式从项数看:完全平方式都是有 项3从每一项看:都有两项可化为两个数(或整式)的平方,
另一项为这两个数(或整式)的乘积的2倍.从符号看:带平方的项符号相同(同“+”或同“-”)a2 ± 2 a b + b2 = ( a ± b )2 否是a表示2y,
b表示3x是a表示(a+b),
b表示1填一填多项式是a表示x,
b表示3关键看能否把多项式化成
“首平方,尾平方,
首尾乘积的两倍在中央”
的形式1、回答:下列各式是不是完全平方式是是是否是否2.填写下表是是不是是不是不是a表示:x
b表示:3
a表示:2y
b表示:1
a表示:2x+y
b表示:3
3、请补上一项,使下列多项式成为完全平方式解:例题 分解因式的方法选择完全平式的特征
“方首平方,尾平方
首尾乘积的
两倍在中央”特征:
1、项数
2、有无公因式可提
3、是否符合公式法要求解:(3)3ax2+6axy+3ay2 解:(4)解:例题 -x2-4y2+4xy 分析:
1、项数
2、有无
公因式可提
3、是否符合
公式法要求
4、各项符号
特征
例6: 分解因式: (1) 3ax2+6axy+3ay2;
(2) (a+b)2-12(a+b)+36.分析:在(1)中有公因式3a,应先提出公因式,再进一步分解。
解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.三、新知识或新方法运用判断因式分解正误。(1) -x2-2xy-y2= -(x-y)2分析:首项(平方项)为负,首先提取“-”号 (2)a2+2ab-b2= (a-b)2分析:完全平方式 平方项符号相同(同正) 1:如何用符号表示完全平方公式?a2+2ab+b2=(a+b)2,
a2-2ab+b2=(a-b)2.2:完全平方公式的结构特点是什么?四、小结完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
简记口诀: 首平方,尾平方,首尾积的2倍在中央。因式分解:(1)25x2+10x+1 解:原式=(5x)2+2×5x×1+12练一练=(5x+1)2 (2)-a2-10a -25解:原式=-(a2+2×a×5+52)因式分解:(3)-a3b3+2a2b3-ab3解:原式=-ab3(a2-2a×1+12)
=-ab3(a-1)2练一练 (4)9 - 12(a-b) + 4 (a-b)2解:原式=32-2×3×2(a-b)+
=
=(3-2a+2b)2练习题:2、下列各式中,能用完全平方公式分解的是( )
A、a2+b2+ab B、a2+2ab-b2
C、a2-ab+2b2 D、-2ab+a2+b2
3、下列各式中,不能用完全平方公式分解的是( )
A、x2+y2-2xy B、x2+4xy+4y2
C、a2-ab+b2 D、-2ab+a2+b2
DC4、下列各式中,能用完全平方公式分解的是( )
A、x2+2xy-y2 B、x2-xy+y2
C、 D、
5、下列各式中,不能用完全平方公式分解的是( )
A、x4+6x2y2+9y4 B、x2n-2xnyn+y2n
C、x6-4x3y3+4y6 D、x4+x2y2+y4
DD6、把 分解因式得
( )
A、 B、
7、把 分解因式得
( )
A、 B、BA8、如果100x2+kxy+y2可以分解为(10x-y)2,那么k的值是( )
A、20 B、-20
C、10 D、-10
9、如果x2+mxy+9y2是一个完全平方式,那么m的值为( )
A、6 B、±6
C、3 D、±3 BB10、把 分解因式得( )
A、 B、
C、 D、
11、计算 的结果是( )
A、 1 B、-1
C、 2 D、-2CA12、请用公式法分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
13、请选择适当的方法分解因式:
(1) ax2+2a2x+a3; (2) -3x2+6xy-3y2.1.已知x2+4x+y2-2y+5=0,求 x-y 的值。解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1=能力提升把下列各式因式分解巩固练习挑战极限:
1、多项式:
(x+y)2-2(x2-y2)+(x-y)2能用完全平方公式分解吗?
2、在括号内补上一项,使多项式成为完全平方式:
X4+4x2+( )=( )2 数学书P :119练习1、2 《导学案》:103--104面练习四、作业再见
