2017-2018学年度第一学期沪科版九年级数学上册第22章相似形单元评估检测试题(含答案)
文档属性
| 名称 | 2017-2018学年度第一学期沪科版九年级数学上册第22章相似形单元评估检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-29 22:03:12 | ||
图片预览



文档简介
2017-2018学年度第一学期沪科版九年级数学上册
第22章 相似形 单元评估检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.由,可得比例式( )
A. B.
C. D.
?2.把长的线段进行黄金分割,则较长线段的长(精确到)是( )
A. B. C. D.
?3.如图,平行于的直线把分成的两部分面积相等,则
A. B. C. D.
?4.如图,已知直线,直线,与,,分别交于点,,,,,,若,,,则的值是( )
A. B. C. D.
?5.小亮同学身高,经太阳照射,在地面上的影长为,此时测得一棵树在同一地面的影长为,则树高为( )
A. B. C. D.
?6.如图,在中,,,平分,则的长为( )
A. B.
C. D.
?7.已知与是关于点的位似图形,它们的对应点到点的距离分别为和,则与的面积比为( )
A. B. C. D.
?
8.在正方形网络图上(如图)有四个三角形,其中与相似(不包本身)的有( )
A.个 B.个 C.个 D.个
?9.如图,在中,,是的中点,的延长线交于,那么的值为( )
A. B. C. D.
?10.如图,是的重心,则下列结论正确的是( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知中,,,,点是边的中点,经过点的直线与另一边交于点,若直线截所得到的三角形与相似,则________.
?12.如图,直线、、…是一组等距的平行线,过直线上的点作两条射线,分别与直线、相交于点、、、.若,则的长是________.
?13.若两个相似三角形对应高的比是,则它们的周长比是________.
?14.如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端、,不断调整站立的位置,使在点处恰好能看到铁塔的顶部和底部,设小明的手臂长,小尺长,点到铁塔底部的距离,则铁塔的高度是________.
?
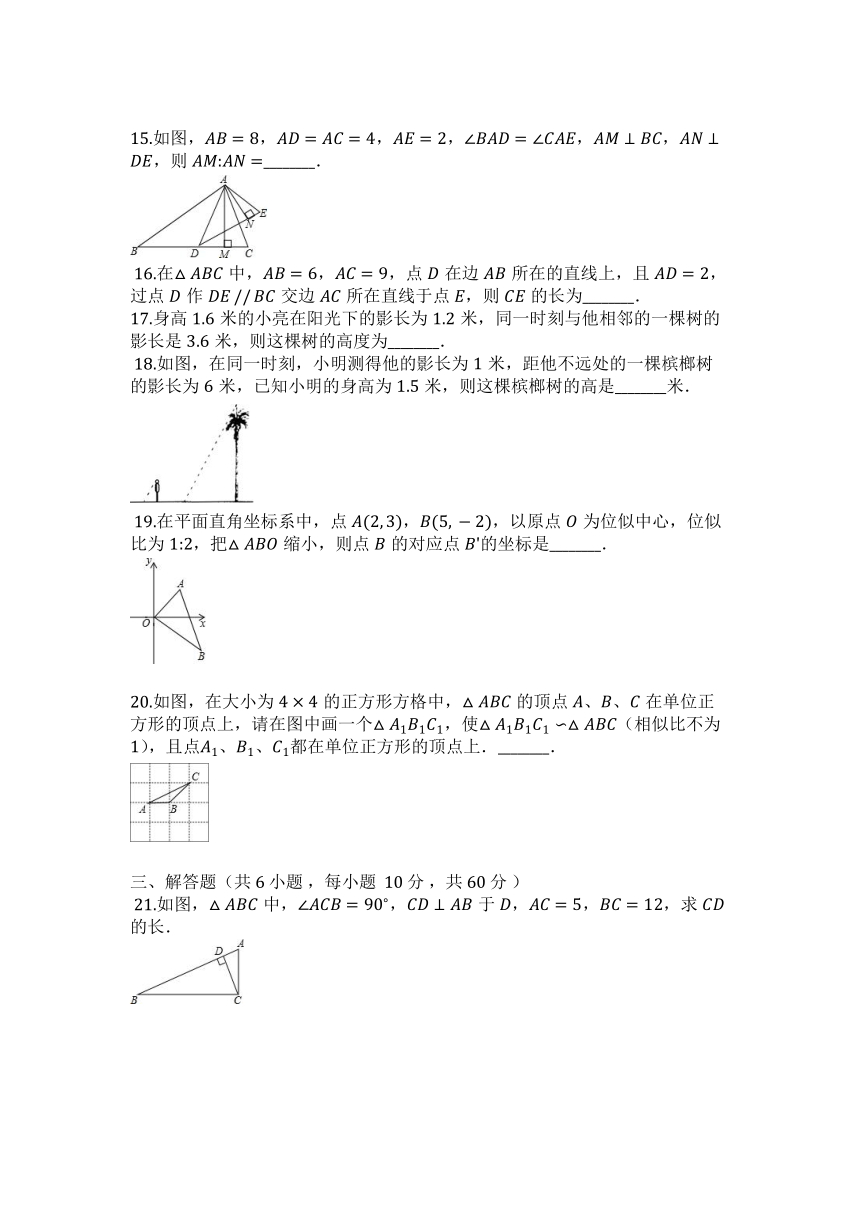
15.如图,,,,,,,则________.
?16.在中,,,点在边所在的直线上,且,过点作交边所在直线于点,则的长为________.?
17.身高米的小亮在阳光下的影长为米,同一时刻与他相邻的一棵树的影长是米,则这棵树的高度为________.
?18.如图,在同一时刻,小明测得他的影长为米,距他不远处的一棵槟榔树的影长为米,已知小明的身高为米,则这棵槟榔树的高是________米.
?19.在平面直角坐标系中,点,,以原点为位似中心,位似比为,把缩小,则点的对应点的坐标是________.
?
20.如图,在大小为的正方形方格中,的顶点、、在单位正方形的顶点上,请在图中画一个,使(相似比不为),且点、、都在单位正方形的顶点上.________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,中,,于,,,求的长.
?
22.如图,以原点为位似中心,把放大后得到,求与的相似比.
?
2
3.如图,,且.
梯形与梯形是否位似?如果位似,求出它们的相似比,如果不位似,说明理由;
若.求梯形的面积.
?
24.如图,图,在的正方形网格中,每个小正方形的边长均为,每个小正方形的顶点叫做格点,的顶点在格点上,按要求画图.
在图中,以点为位似中心画出一个三角形,使它与的位似比为.
在图中,画出一个与相似的,要求所画的三角形的顶点在格点上,与的相似比不为,且与中所画的三角形不相同.
?
25.如图,已知零件的外径为,现用一个交叉卡钳(两条尺长和相等)测量零件的内孔直径,如果.且量得.求以及零件厚度.
?
26.如图所示,已知,,某同学在探索与的关系时,进行了下列探究:
由于,得出;同理;
所以;
因为,所以.
如果,你发现、、、之间存在怎样的关系并说明你的猜想的正确性;
利用你发现的结论,请你通过画图把已知线段分成两部分.
答案
1.D
2.B
3.D
4.B
5.C
6.B
7.B
8.B
9.D
10.B
11.或或
12.
13.
14.
15.
16.或
17.米
18.
19.或
20.答案如图
21.解:如图,∵在中,,,,
∴由勾股定理得到.
又,
∴,即.
则,
∴,
∴,
∴.即的长为.
22.解:∵点的坐标是,点的坐标是,
∴,,
∴,
∵与关于点位似,
∴与的相似比.
23.解:梯形与梯形不位似,
∵,
∴,
∵,
∴,,
∴梯形与梯形不位似;∵,
∴,又,
∴,
∵,
∴,又,
∴,
∴梯形的面积.
24.解:如图所示:即为所求;
如图所示:即为所求.
25.解:∵,(对顶角相等),
∴,
∴,
∴,
∴厚度.
26.解:两条直线被平行线所截,对应线段成比例.即:.
为了把分成两部分,从点出发作一条射线,与有适当的夹角.
上取两点.使单位,单位,(即).
连接.过作的平行线,与相交于.则.
第22章 相似形 单元评估检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.由,可得比例式( )
A. B.
C. D.
?2.把长的线段进行黄金分割,则较长线段的长(精确到)是( )
A. B. C. D.
?3.如图,平行于的直线把分成的两部分面积相等,则
A. B. C. D.
?4.如图,已知直线,直线,与,,分别交于点,,,,,,若,,,则的值是( )
A. B. C. D.
?5.小亮同学身高,经太阳照射,在地面上的影长为,此时测得一棵树在同一地面的影长为,则树高为( )
A. B. C. D.
?6.如图,在中,,,平分,则的长为( )
A. B.
C. D.
?7.已知与是关于点的位似图形,它们的对应点到点的距离分别为和,则与的面积比为( )
A. B. C. D.
?
8.在正方形网络图上(如图)有四个三角形,其中与相似(不包本身)的有( )
A.个 B.个 C.个 D.个
?9.如图,在中,,是的中点,的延长线交于,那么的值为( )
A. B. C. D.
?10.如图,是的重心,则下列结论正确的是( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知中,,,,点是边的中点,经过点的直线与另一边交于点,若直线截所得到的三角形与相似,则________.
?12.如图,直线、、…是一组等距的平行线,过直线上的点作两条射线,分别与直线、相交于点、、、.若,则的长是________.
?13.若两个相似三角形对应高的比是,则它们的周长比是________.
?14.如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端、,不断调整站立的位置,使在点处恰好能看到铁塔的顶部和底部,设小明的手臂长,小尺长,点到铁塔底部的距离,则铁塔的高度是________.
?
15.如图,,,,,,,则________.
?16.在中,,,点在边所在的直线上,且,过点作交边所在直线于点,则的长为________.?
17.身高米的小亮在阳光下的影长为米,同一时刻与他相邻的一棵树的影长是米,则这棵树的高度为________.
?18.如图,在同一时刻,小明测得他的影长为米,距他不远处的一棵槟榔树的影长为米,已知小明的身高为米,则这棵槟榔树的高是________米.
?19.在平面直角坐标系中,点,,以原点为位似中心,位似比为,把缩小,则点的对应点的坐标是________.
?
20.如图,在大小为的正方形方格中,的顶点、、在单位正方形的顶点上,请在图中画一个,使(相似比不为),且点、、都在单位正方形的顶点上.________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,中,,于,,,求的长.
?
22.如图,以原点为位似中心,把放大后得到,求与的相似比.
?
2
3.如图,,且.
梯形与梯形是否位似?如果位似,求出它们的相似比,如果不位似,说明理由;
若.求梯形的面积.
?
24.如图,图,在的正方形网格中,每个小正方形的边长均为,每个小正方形的顶点叫做格点,的顶点在格点上,按要求画图.
在图中,以点为位似中心画出一个三角形,使它与的位似比为.
在图中,画出一个与相似的,要求所画的三角形的顶点在格点上,与的相似比不为,且与中所画的三角形不相同.
?
25.如图,已知零件的外径为,现用一个交叉卡钳(两条尺长和相等)测量零件的内孔直径,如果.且量得.求以及零件厚度.
?
26.如图所示,已知,,某同学在探索与的关系时,进行了下列探究:
由于,得出;同理;
所以;
因为,所以.
如果,你发现、、、之间存在怎样的关系并说明你的猜想的正确性;
利用你发现的结论,请你通过画图把已知线段分成两部分.
答案
1.D
2.B
3.D
4.B
5.C
6.B
7.B
8.B
9.D
10.B
11.或或
12.
13.
14.
15.
16.或
17.米
18.
19.或
20.答案如图
21.解:如图,∵在中,,,,
∴由勾股定理得到.
又,
∴,即.
则,
∴,
∴,
∴.即的长为.
22.解:∵点的坐标是,点的坐标是,
∴,,
∴,
∵与关于点位似,
∴与的相似比.
23.解:梯形与梯形不位似,
∵,
∴,
∵,
∴,,
∴梯形与梯形不位似;∵,
∴,又,
∴,
∵,
∴,又,
∴,
∴梯形的面积.
24.解:如图所示:即为所求;
如图所示:即为所求.
25.解:∵,(对顶角相等),
∴,
∴,
∴,
∴厚度.
26.解:两条直线被平行线所截,对应线段成比例.即:.
为了把分成两部分,从点出发作一条射线,与有适当的夹角.
上取两点.使单位,单位,(即).
连接.过作的平行线,与相交于.则.
