青岛版2018-2019学年度上学期九年级数学期中检测卷(A)(含解析)
文档属性
| 名称 | 青岛版2018-2019学年度上学期九年级数学期中检测卷(A)(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-31 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
青岛版版2018-2019学年九年级(上)期中检测卷(A)
(时间120分钟,满分120分)
一.选择题((本部分15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 对于四条线段a、b、c、d,如果ab=cd,那么( ).
A. = B. = C. = D. =
2.如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )
A.2对 B. 3对 C. 4对 D.5对
3.计算:
A. B. C. D.
4.如图,为估算某河 (?http:?/??/?www.21cnjy.com?)的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
5.在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是( )
A.45° B.60° C.75° D.105°
6.如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( )
A. B. C. D.1
7.直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
8.把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是( )
A.△ABC∽△A′B′C′ B.△ABC与△A′B′C′的各对应角相等
C.△ABC与△A′B′C′的相似比为 D.△ABC与△A′B′C′的相似比为
9.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B.2 C.3 D.3m
10.如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东60°方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )
A.1小时 B.2小时 C.小时 D.2小时
11.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,CM切⊙O于点C,∠BCM=60°,则∠B的正切值是( )
A. B. C. D.
(11) (13)
12.在一个圆中,给出下列命题,其中正确的是( )
A.若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直
B.若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有4个公共点
C.若两条弦所在直线不平行,则这两条弦可能在圆内有公共点
D.若两条弦平行,则这两条弦之间的距离一定小于圆的半径
13. (2018·广东中考)如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( )
A.6 B.7 C.8 D.9
14.如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A. (﹣1)cm2 B. (+1)cm2 C. 1cm2 D. cm2
15.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是
OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. B. C. D.
二.填空题(本部分8个小题,每小题3分,共24分.把最后答案直接填在题中的横线上)
16.四边形ABCD∽四边形,他们的面积之比为36∶25,若四边形的周长为15cm,则四边形ABCD的周长为 cm。
17.如图,添加一个条件: ,使△ADE∽△ACB,(写出一个即可)
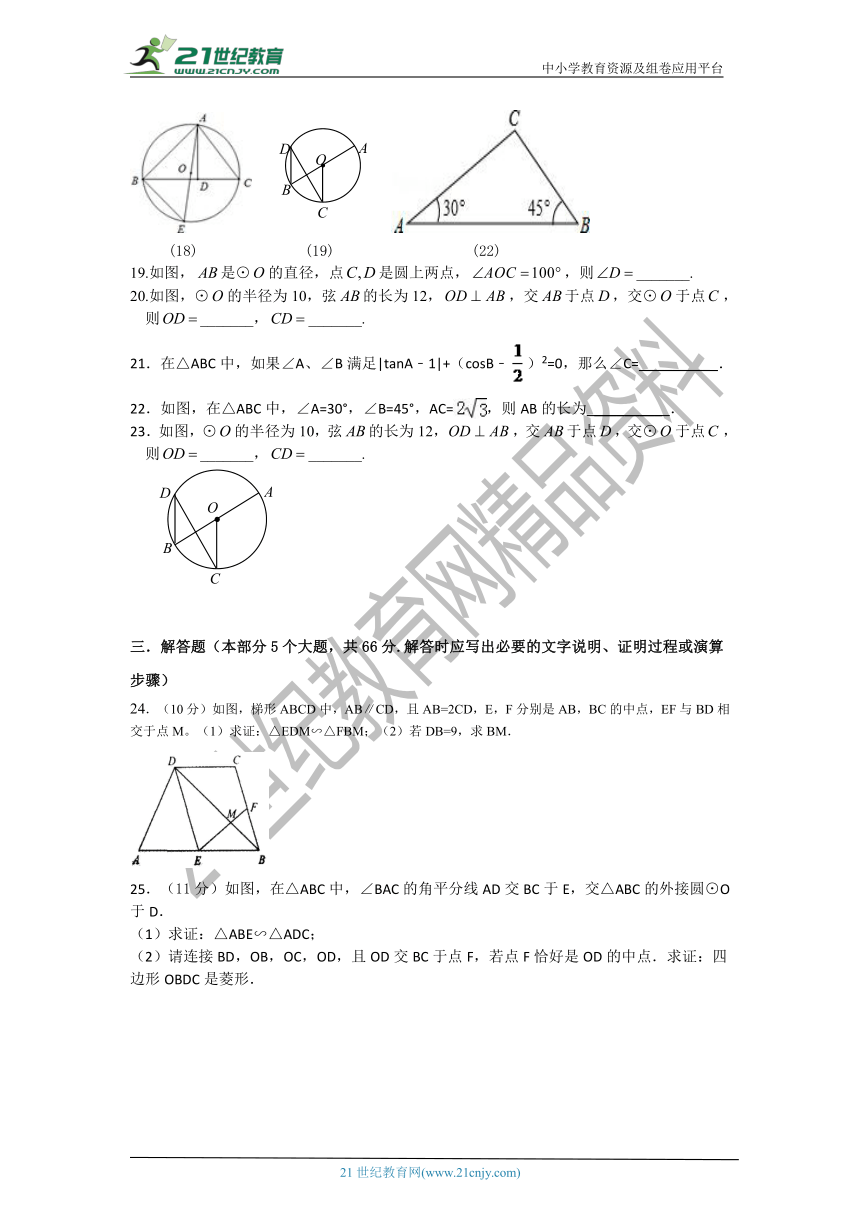
18.如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4,AC=5,AD=4,则⊙O的直径AE= _________ .
(18) (19) (22)
19.如图,是⊙的直径,点是圆上两点,,则_______.
20.如图,⊙的半径为10,弦的长为12,,交于点,交⊙于点,则_______,_______.
21.在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C= _________ .
22.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 _________ .
23.如图,⊙的半径为10,弦的长为12,,交于点,交⊙于点,则_______,_______.
三.解答题(本部分5个大题,共66分.解答时应写出必要的文字说明、证明过程或演算步骤)
24.(10分)如图,梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M。(1)求证:△EDM∽△FBM;(2)若DB=9,求BM.
25.(11分)如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
26.(10分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:,.
27.(10分)如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
28.(10分)如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2,求⊙O的半径.
参考答案
一.选择题(共15小题)
1.B.2.C.3.C.4.B.5.D.6.B.7.A.8.C.9.C.10.B.11.B.12.C.
13.D.14.A.15.B.
二.填空题(共8小题)
16. 18 .17.∠AED=∠B.18. 5 .19.40° .
20. 8、2 .21.75° .22.3+ .23.
三.解答题(共5小题)
24.(1)根据题意及中点的性质得出四边形CBED是平行四边形,根据平行四边形的性质得出∠DEM=∠BFM,∠EDM=∠FBM,从而得出△EDM∽△FBM;(2)3
25.证明:(1)∵∠BAC的角平分线AD,∴∠BAE=∠CAD,
∵∠B=∠D,∴△ABE∽△ADC;
(2)∵∠BAD=∠CAD,∴=,
∵OD为半径,∴DO⊥BC,
∵F为OD的中点,∴OB=BD,OC=CD,
∵OB=OC,∴OB=BD=CD=OC,
∴四边形OBDC是菱形.
26.解:延长PQ交直线AB于点E,(1)∠BPQ=90°﹣60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,则AE=PE=x米;
∵∠PBE=60°∴∠BPE=30°在直角△BPE中,BE=PE=x米,
∵AB=AE﹣BE=6米,则x﹣x=6,解得:x=9+3.则BE=(3+3)米.
在直角△BEQ中,QE=BE=(3+3)=(3+)米.
∴PQ=PE﹣QE=9+3﹣(3+)=6+2≈9(米).
答:电线杆PQ的高度约9米.
(23) (24题图)
27.解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,∴设EF=x,则FC=x,∵CE=20米,
∴x2+(x)2=400,解得:x=10,则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
28.(1)证明:连结OC,如图,
∵=,∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AF,
∵CD⊥AF,∴OC⊥CD,∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵AB为直径,∴∠ACB=90°,
∵==,∴∠BOC=×180°=60°,∴∠BAC=30°,∴∠DAC=30°,
在Rt△ADC中,CD=2,∴AC=2CD=4,
在Rt△ACB中,BC=AC=×4=4,∴AB=2BC=8,∴⊙O的半径为4.
FA
EA
OA
DA
BA
A
C
第15题图
A
O
B
D
C
A
O
B
D
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
