第四章 锐角三角函数单元检测试卷(含解析)
文档属性
| 名称 | 第四章 锐角三角函数单元检测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 173.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 09:09:31 | ||
图片预览


文档简介
湘教版数学九年级上册第四章锐角三角函数单元检测试卷
一、单选题(共10题;共30分)
1.如果α是锐角,且,那么cos(90°﹣α)的值为(?? )
A.?????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
2. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为(?? )
A.?3??????????????????????????????????????? B.???????????????????????????????????????C.????????????????????????????????????????D.?
3. α为锐角,当无意义时,sin(α+15°)+cos(α﹣15°)的值为(? )
A.???????????????????????????????????????B.???????????????????????????????????? C.??????????????????????????????????????D.?
4. 计算:(??? )
A.????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
5. 在△ABC中,∠C=90°,AB=6,cosA= ,则AC等于( ??).
A.?18?????????????????????????????????????????B.?2?????????????????????????????????????? C.????????????????????????????????????? D.?
6. 下列运算结果正确的是
A.?3a3·2a2=6a6???????????????? B.?(-2a)2= -4a2????????????????? C.?tan45°= ???????????????? D.?cos30°=
7. 在△ABC中,∠C=90°, ,那么∠B的度数为(?? )
A.?60°????????????????????????????????????B.?45°????????????????????????????????????C.?30°????????????????????????????????????D.?30°或60°
8. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为(?? )
A. B.1 C. D.
9. 如图,已知 ???? 是 △?????? 的角平分线, ???? 是 ???? 的垂直平分线, ∠??????=90° , ????=3 ,则 ???? 的长为(? ?)
A.?6??????????????????????????????????????????/B.?5??????????????????????????????????????????/C.?4??????????????????????????????????????????/D.?3
3
10. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数(x>0)的图象上,则经过点B的反比例函数解析式为(?? )
A.??????????????????????????? B.??????????????????????????????? C.??????????????????????????? D.?
二、填空题(共8题;共24分)
11. 已知∠A是锐角,且tanA=,则∠A=________.
12. 计算:________.
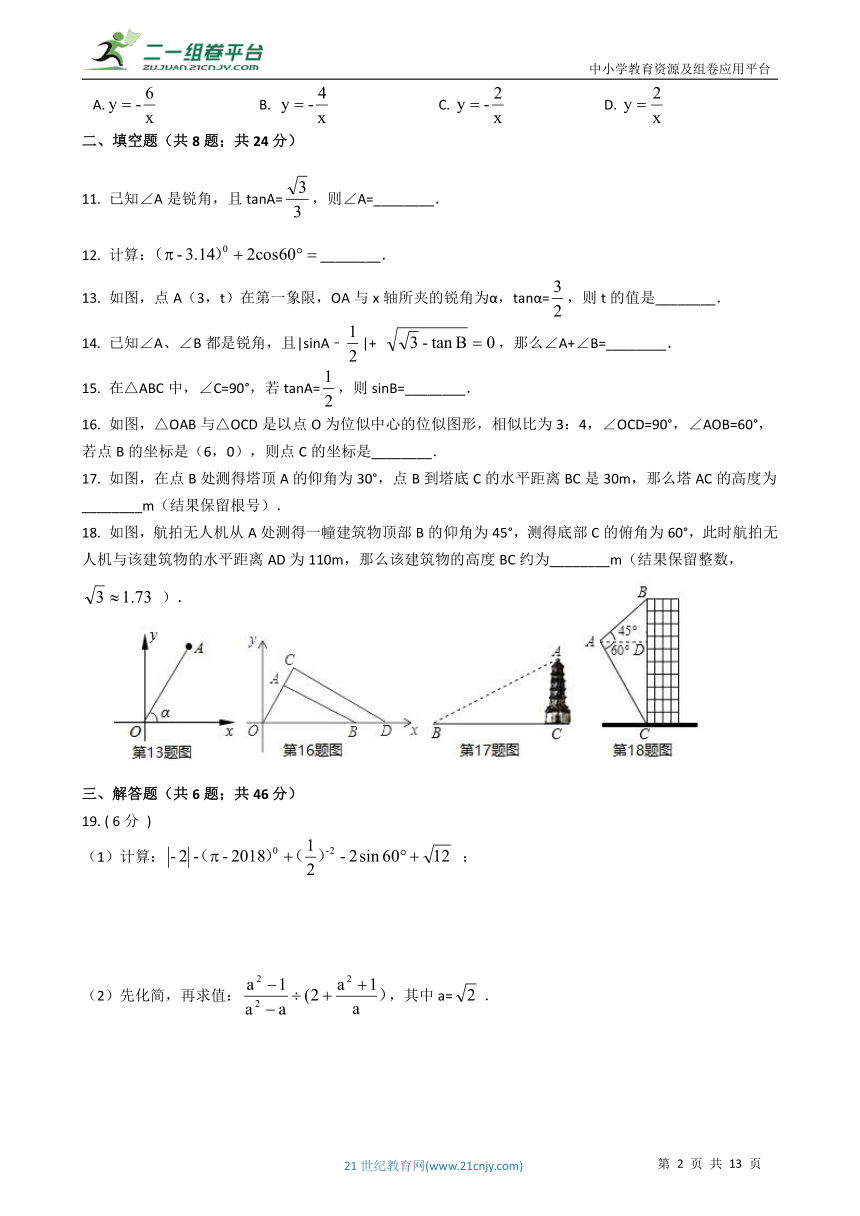
13. 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是________. 14. 已知∠A、∠B都是锐角,且|sinA﹣|+ ,那么∠A+∠B=________.
15. 在△ABC中,∠C=90°,若tanA=,则sinB=________.
16. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________. 17. 如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为________m(结果保留根号). 18. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为________m(结果保留整数, ).
三、解答题(共6题;共46分)
19. ( 6分 ) ? ????????????????????????????????????????????
(1)计算: ;
(2)先化简,再求值:,其中a=?.
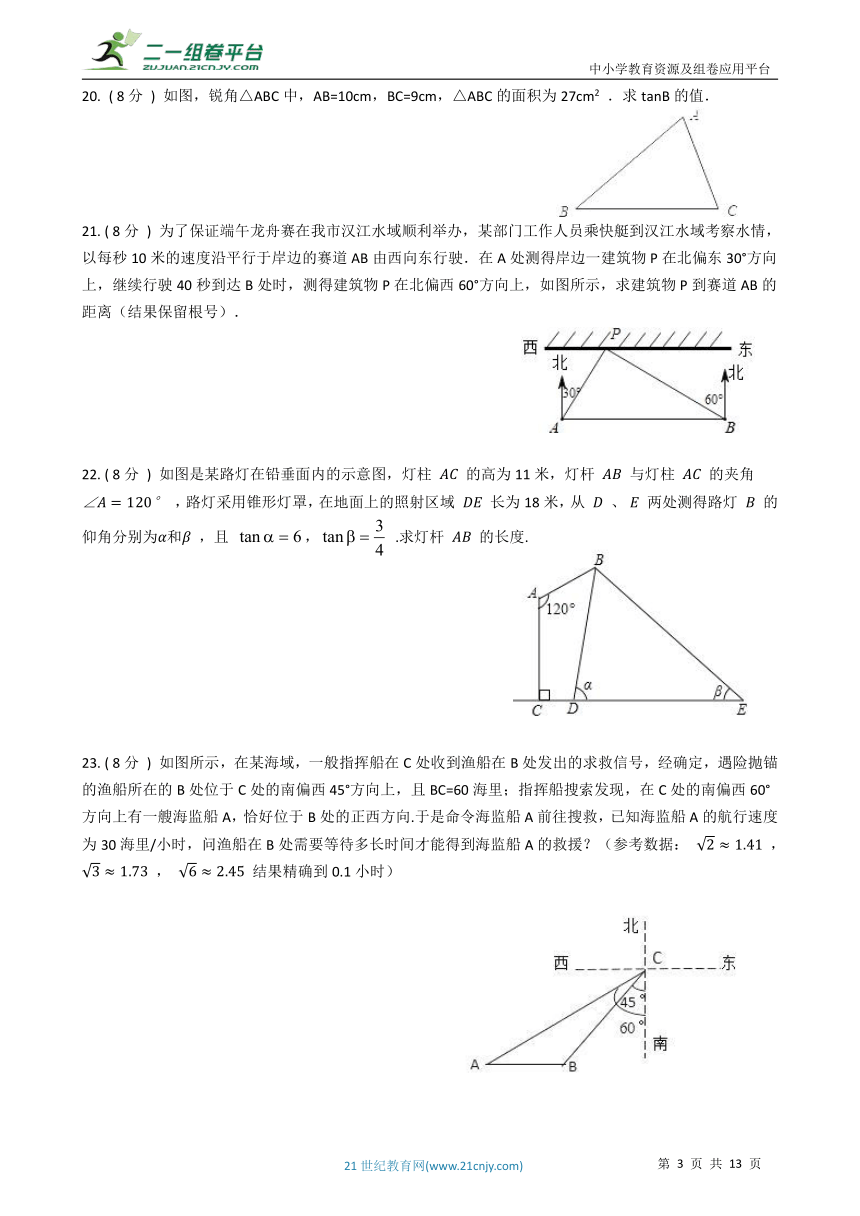
( 8分 ) 如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2 .求tanB的值.
21. ( 8分 ) 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
22. ( 8分 ) 如图是某路灯在铅垂面内的示意图,灯柱 ???? 的高为11米,灯杆 ???? 与灯柱 ???? 的夹角 ∠??=120° ,路灯采用锥形灯罩,在地面上的照射区域 ???? 长为18米,从 ?? 、 ?? 两处测得路灯 ?? 的仰角分别为??和?? ,且 , .求灯杆 ???? 的长度.
23. ( 8分 ) 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:
2
≈1.41 ,
3
≈1.73 ,
6
≈2.45 结果精确到0.1小时)
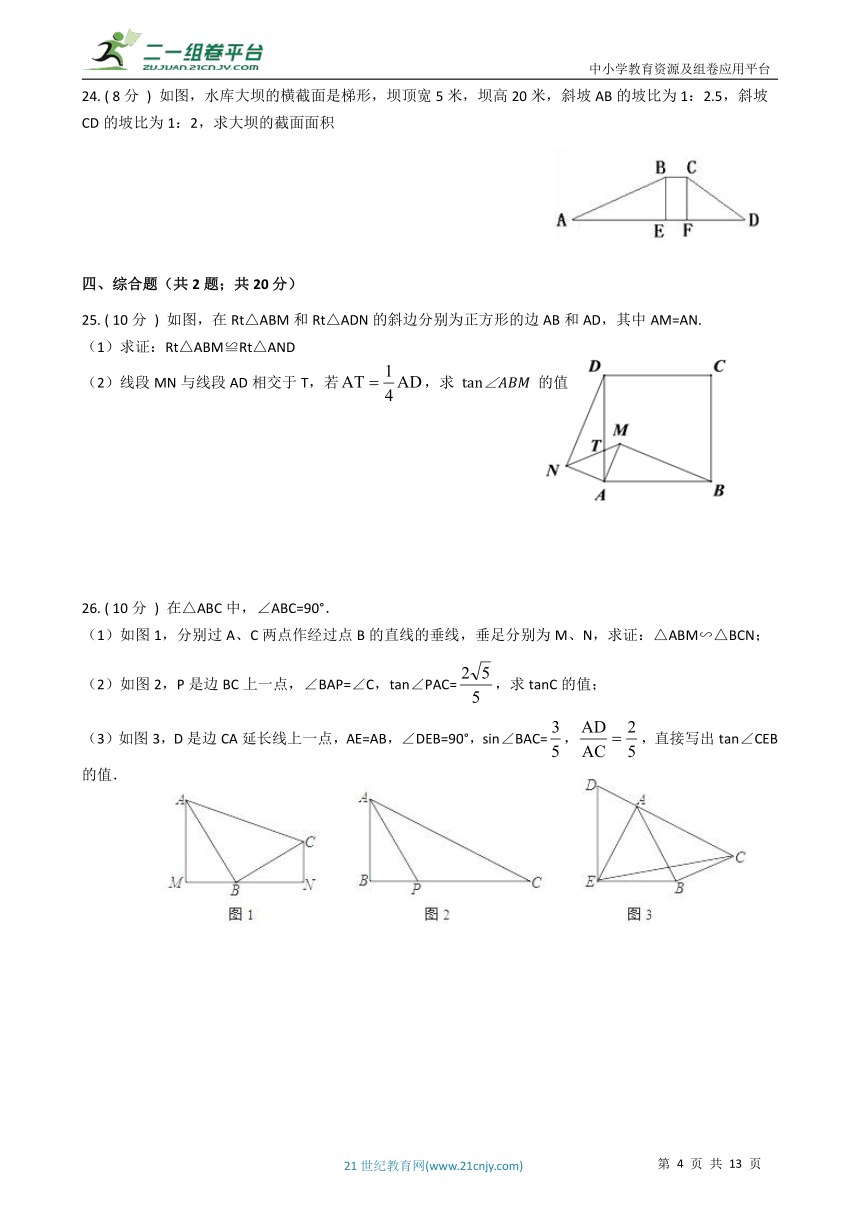
24. ( 8分 ) 如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积 ?
四、综合题(共2题;共20分)
25. ( 10分 ) 如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN. (1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若,求 tan∠?????? 的值
26. ( 10分 ) 在△ABC中,∠ABC=90°. (1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
答案解析部分
一、单选题
1.【答案】B
【解答】解:∵α为锐角,sinα=
3
5
, ∴cos(90°﹣α)=sinα=
3
5
. 故选B. 2.【答案】A
【解答】∵在Rt△ABC中,∠C=90°,AC=1,BC=3, ∴∠A的正切值为
????
????
=
3
1
=3, 故答案为:A. 3.【答案】A
【解答】解:根据题意得1-tanα=0 ∴α=45° ∴sin(α+15°)+cos(α﹣15°)= =sin60°+cos30°=
3
2
+
3
2
=
3
故答案为:A
4.【答案】C
【解答】(
1
2
)﹣1+tan30°?sin60° =2+
3
3
×
3
2
=2+
1
2
=
5
2
, 故答案为:C. 5.【答案】B
【解答】在Rt△ABC中,∠C=90°,cosA=
????
????
=
1
3
,又AB=6,所以AC=2. 故答案为:B. 6.【答案】D
【解答】A、原式=6a5 , 故不符合题意; B、原式=4a2 , 故不符合题意; C、原式=1,故不符合题意; D、原式=
3
2
,故符合题意. 故答案为:D
7.【答案】C
【解答】∵ cos??=
1
2
, ∴∠A=60°. ∵∠C=90°, ∴∠B=90°-60°=30°. 8.【答案】B
【解答】如图,连接BC, / 由网格可得AB=BC=
5
,AC=
10
,即AB2+BC2=AC2 , ∴△ABC为等腰直角三角形, ∴∠BAC=45°, 则tan∠BAC=1, 故答案为:B. 9.【答案】D
【解答】解:∵ED是BC的垂直平分线, ∴DB=DC, ∴∠C=∠DBC, ∵BD是△ABC的角平分线, ∴∠ABD=∠DBC, ∵∠A=90°,∴∠C+∠ABD+∠DBC=90°, ∴∠C=∠DBC=∠ABD=30°, ∴BD=2AD=6, ∴CD=6, ∴CE=CD×cos∠C= 3
3
, 故答案为:D 10.【答案】C
【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D, / ∵∠BOA=90°, ∴∠BOC+∠AOD=90°, ∵∠AOD+∠OAD=90°, ∴∠BOC=∠OAD, 又∵∠BCO=∠ADO=90°, ∴△BCO∽△ODA, ∴
????
????
=tan30°=
3
3
, ∴
??
△??????
??
△??????
=
1
3
, ∵
1
2
×AD×DO=
1
2
xy=3, ∴S△BCO=
1
2
×BC×CO=
1
3
S△AOD=1, ∴S△AOD=2, ∵经过点B的反比例函数图象在第二象限, 故反比例函数解析式为:y=﹣
2
??
. 故答案为:C.
二、填空题
11.【答案】30°
【解答】解:∵∠A是锐角,tanA=
3
3
,∴∠A=30°.故答案为:30°.
12.【答案】2
【解答】原式=1+2×
1
2
, =1+1, =2. 故答案为:2. 13.【答案】
9
2
【解答】过点A作AB⊥x轴于B, / ∵点A(3,t)在第一象限,∴AB=t,OB=3,又∵tanα=
????
????
=
??
3
=
3
2
, ∴t=
9
2
. 14.【答案】90°
【解答】解:由题意可知:sinA=
1
2
,tanB=
3
, ∴∠A=30°,∠B=60°, ∴∠A+∠B=90° 故答案为:90° 15.【答案】
2
5
5
【解答】解:如图所示: / ∵∠C=90°,tanA=
1
2
, ∴设BC=x,则AC=2x,故AB=
5
x, 则sinB=
????
????
=
2??
5
??
=
2
5
5
. 故答案为:
2
5
5
?. 16.【答案】(2,2
3
)
【解答】解:分别过A作AE⊥OB,CF⊥OB, / ∵∠OCD=90°,∠AOB=60°, ∴∠ABO=∠CDO=30°,∠OCF=30°, ∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0), ∴D(8,0),则DO=8, 故OC=4, 则FO=2,CF=CO?cos30°=4×
3
2
=2
3
, 故点C的坐标是:(2,2
3
). 故答案为:(2,2
3
). 17.【答案】10
3
【解答】解:∵在点B处测得塔顶A的仰角为30°, ∴∠B=30°, ∵BC=30m, ∴tan∠B=
????
????
=
3
3
? ∴AC=
3
3
BC=30×
3
3
=10
3
m, 故答案为:10
3
. 18.【答案】300
【解答】如图,∵在Rt△ABD中,AD=110,∠BAD=45°, ∴BD= AD?tan45° =110(m), ∵在Rt△ACD中,∠CAD=60°, ∴CD=AD?tan60°=110×
3
≈190(m), ∴BC=BD+CD=110+190=300(m), 即该建筑物的高度BC约为300米, 故答案为:300.
三、解答题
19.【答案】(1)解:原式=2﹣1+4﹣2×
3
2
+2
3
=2﹣1+4﹣
3
+2
3
=5+
3
(2)解:原式=
(??+1)(???1)
??(???1)
÷
2??+
??
2
+1
??
=
(??+1)(???1)
??(???1)
·
??
(??+1)
2
=
1
??+1
, 当a=
2
时,原式=
1
2
+1
=
2
-1
20.【答案】解:过点A作AH⊥BC于H, / ∵S△ABC=27, ∴
1
2
×9×????=27 , ∴AH=6, ∵AB=10, ∴BH=
??
??
2
???
??
2
=
10
2
?
6
2
=8, ∴tanB=
????
????
=
6
8
=
3
4
.
21.【答案】解:如图,过P点作PC⊥AB于C, / 由题意可知:∠PAC=60°,∠PBC=30°, 在Rt△PAC中,tan∠PAC=
????
????
,∴AC=
3
3
PC, 在Rt△PBC中,tan∠PBC=
????
????
,∴BC=
3
PC, ∵AB=AC+BC=
3
3
PC+
3
PC=10×40=400, ∴PC=100
3
, 答:建筑物P到赛道AB的距离为100
3
米
22.【答案】解:过点B作BF⊥CE于点F,过点作AG⊥BF于点G/ ∴AG=CF,AC=FG=11 ∵∠BAC=120°,∠GAC=90° ∴∠BAG=120°-90°=30° 设BF=x 在Rt△BDF中, tan??=
????
????
=6,即????=
??
6
在Rt△BEF中, tan??=
????
????
=
3
4
,即????=
4
3
?? ∵DE=DF+EF ∴
??
6
+
4
3
??=18 解之:x=12 ∴BG=BF-GF=12-11=1 在Rt△ABG中,∠BAG=30° ∴AB=2BG=2
23.【答案】解:因为A在B的正西方,延长AB交南北轴于点D,则AB⊥CD于点D/ ∵∠BCD=45°,BD⊥CD ∴BD=CD 在Rt△BDC中,∵cos∠BCD=
????
????
,BC=60海里 即cos45°=
????
60
=
2
2
,解得CD= 30
2
海里 ∴BD=CD= 30
2
海里 在Rt△ADC中,∵tan∠ACD=
????
????
即 tan60°=
????
30
2
=
3
,解得AD= 30
6
海里??????????? ∵AB=AD-BD ∴AB= 30
6
- 30
2
=30(
6
?
2
)海里 ∵海监船A的航行速度为30海里/小时 则渔船在B处需要等待的时间为
????
30
=
30(
6
?
2
)
30
=
6
?
2
≈2.45-1.41=1.04≈1.0小时 ∴渔船在B处需要等待1.0小时
24.【答案】解:∵斜坡AB的坡度i=1:2.5,∴
????
????
=
1
2.5
, ∵斜坡CD的坡度i=1:2,∴
????
????
=
1
2
, ∵BE=20米,∴AE=50米,DF=40米, ∵EF=BC,BC=5米, ∴EF=5米, ∴AD=AE+EF+DF=50+5+40=95米 ∴S梯形ABCD=
1
2
?(AD+BC)×BE=
1
2
×100×20=1000(平方米)
四、综合题
25.【答案】(1)解:∵AD=AB,AM=AN,∠AMB=∠AND=90° ∴Rt△ABM≌Rt△AND(HL)? (2)解:由Rt△ABM≌Rt△AND易得:∠DAN=∠BAM,DN=BM ∵∠BAM+∠DAM=90°;∠DAN+∠ADN=90° ∴∠DAM=∠AND ∴ND∥AM ∴△DNT∽△AMT ∴
????
????
=
????
????
∵AT=
1
4
AD , ∴
????
????
=
1
3
∵Rt△ABM ∴tan∠ABM=
????
????
=
????
????
=
1
3
??????????????????
26.【答案】(1)解:∵AM⊥MN,CN⊥MN, ∴∠AMB=∠BNC=90°, ∴∠BAM+∠ABM=90°, ∵∠ABC=90°, ∴∠ABM+∠CBN=90°, ∴∠BAM=∠CBN, ∵∠AMB=∠NBC, ∴△ABM∽△BCN (2)解:如图2,过点P作PM⊥AP交AC于M,PN⊥AM于N. / ∵∠BAP+∠1=∠CPM+∠1=90°, ∴∠BAP=∠CPM=∠C, ∴MP=MC ∵tan∠PAC=
????
????
=
2
5
5
=
2
5
=
????
????
, 设MN=2m,PN=
5
m, 根据勾股定理得,PM=
??
??
2
+??
??
2
=3??=????, ∴tanC=
????
????
=
5
??
5??
=
5
5
(3)解:在Rt△ABC中,sin∠BAC=
????
????
=
3
5
, 过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H, / ∵∠DEB=90°, ∴CH∥AG∥DE, ∴
????
????
=
????
????
=
5
2
同(1)的方法得,△ABG∽△BCH??? ∴
????
????
=
????
????
=
????
????
=
4
3
, 设BG=4m,CH=3m,AG=4n,BH=3n, ∵AB=AE,AG⊥BE, ∴EG=BG=4m, ∴GH=BG+BH=4m+3n, ∴
4??+3??
4??
=
5
2
, ∴n=2m, ∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m, 在Rt△CEH中,tan∠BEC=
????
????
=
3
14
/
一、单选题(共10题;共30分)
1.如果α是锐角,且,那么cos(90°﹣α)的值为(?? )
A.?????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
2. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为(?? )
A.?3??????????????????????????????????????? B.???????????????????????????????????????C.????????????????????????????????????????D.?
3. α为锐角,当无意义时,sin(α+15°)+cos(α﹣15°)的值为(? )
A.???????????????????????????????????????B.???????????????????????????????????? C.??????????????????????????????????????D.?
4. 计算:(??? )
A.????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
5. 在△ABC中,∠C=90°,AB=6,cosA= ,则AC等于( ??).
A.?18?????????????????????????????????????????B.?2?????????????????????????????????????? C.????????????????????????????????????? D.?
6. 下列运算结果正确的是
A.?3a3·2a2=6a6???????????????? B.?(-2a)2= -4a2????????????????? C.?tan45°= ???????????????? D.?cos30°=
7. 在△ABC中,∠C=90°, ,那么∠B的度数为(?? )
A.?60°????????????????????????????????????B.?45°????????????????????????????????????C.?30°????????????????????????????????????D.?30°或60°
8. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为(?? )
A. B.1 C. D.
9. 如图,已知 ???? 是 △?????? 的角平分线, ???? 是 ???? 的垂直平分线, ∠??????=90° , ????=3 ,则 ???? 的长为(? ?)
A.?6??????????????????????????????????????????/B.?5??????????????????????????????????????????/C.?4??????????????????????????????????????????/D.?3
3
10. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数(x>0)的图象上,则经过点B的反比例函数解析式为(?? )
A.??????????????????????????? B.??????????????????????????????? C.??????????????????????????? D.?
二、填空题(共8题;共24分)
11. 已知∠A是锐角,且tanA=,则∠A=________.
12. 计算:________.
13. 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是________. 14. 已知∠A、∠B都是锐角,且|sinA﹣|+ ,那么∠A+∠B=________.
15. 在△ABC中,∠C=90°,若tanA=,则sinB=________.
16. 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是________. 17. 如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为________m(结果保留根号). 18. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为________m(结果保留整数, ).
三、解答题(共6题;共46分)
19. ( 6分 ) ? ????????????????????????????????????????????
(1)计算: ;
(2)先化简,再求值:,其中a=?.
( 8分 ) 如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2 .求tanB的值.
21. ( 8分 ) 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
22. ( 8分 ) 如图是某路灯在铅垂面内的示意图,灯柱 ???? 的高为11米,灯杆 ???? 与灯柱 ???? 的夹角 ∠??=120° ,路灯采用锥形灯罩,在地面上的照射区域 ???? 长为18米,从 ?? 、 ?? 两处测得路灯 ?? 的仰角分别为??和?? ,且 , .求灯杆 ???? 的长度.
23. ( 8分 ) 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:
2
≈1.41 ,
3
≈1.73 ,
6
≈2.45 结果精确到0.1小时)
24. ( 8分 ) 如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积 ?
四、综合题(共2题;共20分)
25. ( 10分 ) 如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN. (1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若,求 tan∠?????? 的值
26. ( 10分 ) 在△ABC中,∠ABC=90°. (1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
答案解析部分
一、单选题
1.【答案】B
【解答】解:∵α为锐角,sinα=
3
5
, ∴cos(90°﹣α)=sinα=
3
5
. 故选B. 2.【答案】A
【解答】∵在Rt△ABC中,∠C=90°,AC=1,BC=3, ∴∠A的正切值为
????
????
=
3
1
=3, 故答案为:A. 3.【答案】A
【解答】解:根据题意得1-tanα=0 ∴α=45° ∴sin(α+15°)+cos(α﹣15°)= =sin60°+cos30°=
3
2
+
3
2
=
3
故答案为:A
4.【答案】C
【解答】(
1
2
)﹣1+tan30°?sin60° =2+
3
3
×
3
2
=2+
1
2
=
5
2
, 故答案为:C. 5.【答案】B
【解答】在Rt△ABC中,∠C=90°,cosA=
????
????
=
1
3
,又AB=6,所以AC=2. 故答案为:B. 6.【答案】D
【解答】A、原式=6a5 , 故不符合题意; B、原式=4a2 , 故不符合题意; C、原式=1,故不符合题意; D、原式=
3
2
,故符合题意. 故答案为:D
7.【答案】C
【解答】∵ cos??=
1
2
, ∴∠A=60°. ∵∠C=90°, ∴∠B=90°-60°=30°. 8.【答案】B
【解答】如图,连接BC, / 由网格可得AB=BC=
5
,AC=
10
,即AB2+BC2=AC2 , ∴△ABC为等腰直角三角形, ∴∠BAC=45°, 则tan∠BAC=1, 故答案为:B. 9.【答案】D
【解答】解:∵ED是BC的垂直平分线, ∴DB=DC, ∴∠C=∠DBC, ∵BD是△ABC的角平分线, ∴∠ABD=∠DBC, ∵∠A=90°,∴∠C+∠ABD+∠DBC=90°, ∴∠C=∠DBC=∠ABD=30°, ∴BD=2AD=6, ∴CD=6, ∴CE=CD×cos∠C= 3
3
, 故答案为:D 10.【答案】C
【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D, / ∵∠BOA=90°, ∴∠BOC+∠AOD=90°, ∵∠AOD+∠OAD=90°, ∴∠BOC=∠OAD, 又∵∠BCO=∠ADO=90°, ∴△BCO∽△ODA, ∴
????
????
=tan30°=
3
3
, ∴
??
△??????
??
△??????
=
1
3
, ∵
1
2
×AD×DO=
1
2
xy=3, ∴S△BCO=
1
2
×BC×CO=
1
3
S△AOD=1, ∴S△AOD=2, ∵经过点B的反比例函数图象在第二象限, 故反比例函数解析式为:y=﹣
2
??
. 故答案为:C.
二、填空题
11.【答案】30°
【解答】解:∵∠A是锐角,tanA=
3
3
,∴∠A=30°.故答案为:30°.
12.【答案】2
【解答】原式=1+2×
1
2
, =1+1, =2. 故答案为:2. 13.【答案】
9
2
【解答】过点A作AB⊥x轴于B, / ∵点A(3,t)在第一象限,∴AB=t,OB=3,又∵tanα=
????
????
=
??
3
=
3
2
, ∴t=
9
2
. 14.【答案】90°
【解答】解:由题意可知:sinA=
1
2
,tanB=
3
, ∴∠A=30°,∠B=60°, ∴∠A+∠B=90° 故答案为:90° 15.【答案】
2
5
5
【解答】解:如图所示: / ∵∠C=90°,tanA=
1
2
, ∴设BC=x,则AC=2x,故AB=
5
x, 则sinB=
????
????
=
2??
5
??
=
2
5
5
. 故答案为:
2
5
5
?. 16.【答案】(2,2
3
)
【解答】解:分别过A作AE⊥OB,CF⊥OB, / ∵∠OCD=90°,∠AOB=60°, ∴∠ABO=∠CDO=30°,∠OCF=30°, ∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0), ∴D(8,0),则DO=8, 故OC=4, 则FO=2,CF=CO?cos30°=4×
3
2
=2
3
, 故点C的坐标是:(2,2
3
). 故答案为:(2,2
3
). 17.【答案】10
3
【解答】解:∵在点B处测得塔顶A的仰角为30°, ∴∠B=30°, ∵BC=30m, ∴tan∠B=
????
????
=
3
3
? ∴AC=
3
3
BC=30×
3
3
=10
3
m, 故答案为:10
3
. 18.【答案】300
【解答】如图,∵在Rt△ABD中,AD=110,∠BAD=45°, ∴BD= AD?tan45° =110(m), ∵在Rt△ACD中,∠CAD=60°, ∴CD=AD?tan60°=110×
3
≈190(m), ∴BC=BD+CD=110+190=300(m), 即该建筑物的高度BC约为300米, 故答案为:300.
三、解答题
19.【答案】(1)解:原式=2﹣1+4﹣2×
3
2
+2
3
=2﹣1+4﹣
3
+2
3
=5+
3
(2)解:原式=
(??+1)(???1)
??(???1)
÷
2??+
??
2
+1
??
=
(??+1)(???1)
??(???1)
·
??
(??+1)
2
=
1
??+1
, 当a=
2
时,原式=
1
2
+1
=
2
-1
20.【答案】解:过点A作AH⊥BC于H, / ∵S△ABC=27, ∴
1
2
×9×????=27 , ∴AH=6, ∵AB=10, ∴BH=
??
??
2
???
??
2
=
10
2
?
6
2
=8, ∴tanB=
????
????
=
6
8
=
3
4
.
21.【答案】解:如图,过P点作PC⊥AB于C, / 由题意可知:∠PAC=60°,∠PBC=30°, 在Rt△PAC中,tan∠PAC=
????
????
,∴AC=
3
3
PC, 在Rt△PBC中,tan∠PBC=
????
????
,∴BC=
3
PC, ∵AB=AC+BC=
3
3
PC+
3
PC=10×40=400, ∴PC=100
3
, 答:建筑物P到赛道AB的距离为100
3
米
22.【答案】解:过点B作BF⊥CE于点F,过点作AG⊥BF于点G/ ∴AG=CF,AC=FG=11 ∵∠BAC=120°,∠GAC=90° ∴∠BAG=120°-90°=30° 设BF=x 在Rt△BDF中, tan??=
????
????
=6,即????=
??
6
在Rt△BEF中, tan??=
????
????
=
3
4
,即????=
4
3
?? ∵DE=DF+EF ∴
??
6
+
4
3
??=18 解之:x=12 ∴BG=BF-GF=12-11=1 在Rt△ABG中,∠BAG=30° ∴AB=2BG=2
23.【答案】解:因为A在B的正西方,延长AB交南北轴于点D,则AB⊥CD于点D/ ∵∠BCD=45°,BD⊥CD ∴BD=CD 在Rt△BDC中,∵cos∠BCD=
????
????
,BC=60海里 即cos45°=
????
60
=
2
2
,解得CD= 30
2
海里 ∴BD=CD= 30
2
海里 在Rt△ADC中,∵tan∠ACD=
????
????
即 tan60°=
????
30
2
=
3
,解得AD= 30
6
海里??????????? ∵AB=AD-BD ∴AB= 30
6
- 30
2
=30(
6
?
2
)海里 ∵海监船A的航行速度为30海里/小时 则渔船在B处需要等待的时间为
????
30
=
30(
6
?
2
)
30
=
6
?
2
≈2.45-1.41=1.04≈1.0小时 ∴渔船在B处需要等待1.0小时
24.【答案】解:∵斜坡AB的坡度i=1:2.5,∴
????
????
=
1
2.5
, ∵斜坡CD的坡度i=1:2,∴
????
????
=
1
2
, ∵BE=20米,∴AE=50米,DF=40米, ∵EF=BC,BC=5米, ∴EF=5米, ∴AD=AE+EF+DF=50+5+40=95米 ∴S梯形ABCD=
1
2
?(AD+BC)×BE=
1
2
×100×20=1000(平方米)
四、综合题
25.【答案】(1)解:∵AD=AB,AM=AN,∠AMB=∠AND=90° ∴Rt△ABM≌Rt△AND(HL)? (2)解:由Rt△ABM≌Rt△AND易得:∠DAN=∠BAM,DN=BM ∵∠BAM+∠DAM=90°;∠DAN+∠ADN=90° ∴∠DAM=∠AND ∴ND∥AM ∴△DNT∽△AMT ∴
????
????
=
????
????
∵AT=
1
4
AD , ∴
????
????
=
1
3
∵Rt△ABM ∴tan∠ABM=
????
????
=
????
????
=
1
3
??????????????????
26.【答案】(1)解:∵AM⊥MN,CN⊥MN, ∴∠AMB=∠BNC=90°, ∴∠BAM+∠ABM=90°, ∵∠ABC=90°, ∴∠ABM+∠CBN=90°, ∴∠BAM=∠CBN, ∵∠AMB=∠NBC, ∴△ABM∽△BCN (2)解:如图2,过点P作PM⊥AP交AC于M,PN⊥AM于N. / ∵∠BAP+∠1=∠CPM+∠1=90°, ∴∠BAP=∠CPM=∠C, ∴MP=MC ∵tan∠PAC=
????
????
=
2
5
5
=
2
5
=
????
????
, 设MN=2m,PN=
5
m, 根据勾股定理得,PM=
??
??
2
+??
??
2
=3??=????, ∴tanC=
????
????
=
5
??
5??
=
5
5
(3)解:在Rt△ABC中,sin∠BAC=
????
????
=
3
5
, 过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H, / ∵∠DEB=90°, ∴CH∥AG∥DE, ∴
????
????
=
????
????
=
5
2
同(1)的方法得,△ABG∽△BCH??? ∴
????
????
=
????
????
=
????
????
=
4
3
, 设BG=4m,CH=3m,AG=4n,BH=3n, ∵AB=AE,AG⊥BE, ∴EG=BG=4m, ∴GH=BG+BH=4m+3n, ∴
4??+3??
4??
=
5
2
, ∴n=2m, ∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m, 在Rt△CEH中,tan∠BEC=
????
????
=
3
14
/
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
