必修2 第一章 空间几何体 45分钟(拔高)训练题
文档属性
| 名称 | 必修2 第一章 空间几何体 45分钟(拔高)训练题 |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 08:48:32 | ||
图片预览


文档简介
第一章 空间几何体 45分钟(拔高)训练题
1.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.
2.若一个正三棱锥的底面正三角形的边长为4,侧棱长为8.求其表面积和体积。
3.长方体AC1的长、宽、高分别为3、2、1,从A到C1沿长方体的表面的最短距离为________.
4.已知球面上有A、B、C三点,如果AB=AC=BC=2 , 球心到面ABC的距离为1,那么球的体积________
5.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?
6.根据如图所示的几何体的表面展开图,画出立体图形.
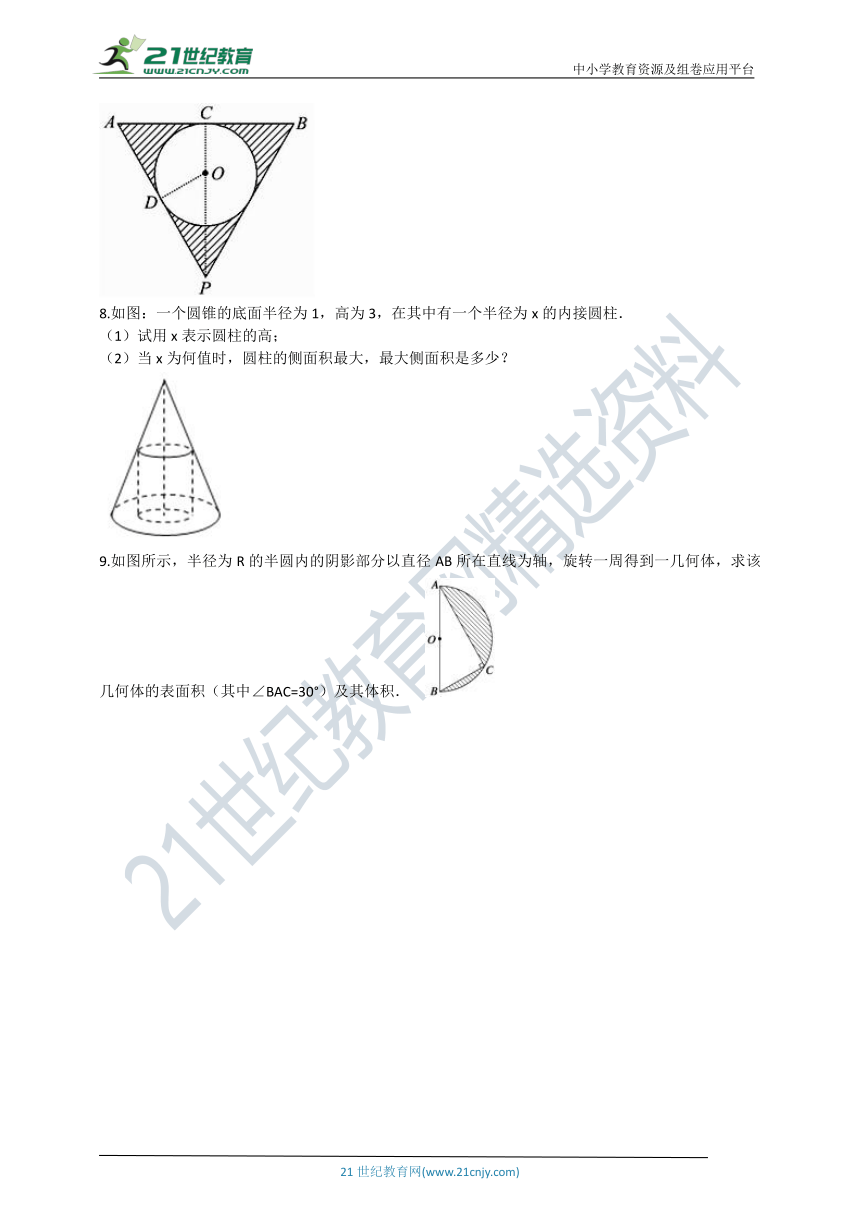
7.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
8.如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱. (1)试用x表示圆柱的高; (2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
9.如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
答案解析部分
1.B 【解析】:如图为等腰直角三角形旋转而成的旋转体, , 故答案为:B. 3.【答案】 【解析】:结合长方体的三种展开图不难求得AC1的长分别是: = , = , = 显然最小值是 . 故答案为 . 4. 解: 由题意,AB=AC=BC=2 , 所以△ABC的外接圆的半径为2,因为球心到平面ABC的距离为1,所以球的半径是:R= , 球的体积是:πR3= . 故答案为: . 5.解:由于正视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块,即最多要17块. 而搭建这样的几何体用小立方体个数最少的情况是每列只要有一个最大的数字,其他方框内的数可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块,即最少要11块.
6.解:图1是以ABCD为底面,P为顶点的四棱锥.图2是以ABCD和A1B1C1D1为底面的棱柱.其图形如图所示.
7.解:如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r , 水面半径BC的长为 r , 则容器内水的体积为V=V圆锥-V球= ( r)2·3r- r3= r3 , 将球取出后,设容器中水的深度为h , 则水面圆的半径为 h , 从而容器内水的体积为V′= 2h= h3 , 由V=V′,得h= r.
8.解:(1)设所求的圆柱的底面半径为x,它的轴截面如图:BO=1,PO=3,圆柱的高为:h 由图得,,即h=3﹣3x. (2)S圆柱侧=2πhx=2π(3﹣3x)x=6π(x﹣x2),当x=时,函数取得最大值为:. ∴当圆柱的底面半径为时,它的侧面积最大为
9.解:如图所示,过C作CO1⊥AB于O1 , 在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R, ∴AC= R,BC=R,CO1= R,∴S球=4πR2 , =π× R× R= πR2 , =π× R×R= πR2 , ∴S几何体表=S球+ + = πR2 , ∴旋转所得到的几何体的表面积为 πR2 . 又V球= πR3 , = ?AO1?π?CO12= πR2?AO1 = BO1?πCO12= BO1?πR2∴V几何体=V球﹣( + )= πR3 .
1.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.
2.若一个正三棱锥的底面正三角形的边长为4,侧棱长为8.求其表面积和体积。
3.长方体AC1的长、宽、高分别为3、2、1,从A到C1沿长方体的表面的最短距离为________.
4.已知球面上有A、B、C三点,如果AB=AC=BC=2 , 球心到面ABC的距离为1,那么球的体积________
5.用小立方体搭成一个几何体,使它的正视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?
6.根据如图所示的几何体的表面展开图,画出立体图形.
7.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
8.如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱. (1)试用x表示圆柱的高; (2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
9.如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
答案解析部分
1.B 【解析】:如图为等腰直角三角形旋转而成的旋转体, , 故答案为:B. 3.【答案】 【解析】:结合长方体的三种展开图不难求得AC1的长分别是: = , = , = 显然最小值是 . 故答案为 . 4. 解: 由题意,AB=AC=BC=2 , 所以△ABC的外接圆的半径为2,因为球心到平面ABC的距离为1,所以球的半径是:R= , 球的体积是:πR3= . 故答案为: . 5.解:由于正视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块,即最多要17块. 而搭建这样的几何体用小立方体个数最少的情况是每列只要有一个最大的数字,其他方框内的数可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块,即最少要11块.
6.解:图1是以ABCD为底面,P为顶点的四棱锥.图2是以ABCD和A1B1C1D1为底面的棱柱.其图形如图所示.
7.解:如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r , 水面半径BC的长为 r , 则容器内水的体积为V=V圆锥-V球= ( r)2·3r- r3= r3 , 将球取出后,设容器中水的深度为h , 则水面圆的半径为 h , 从而容器内水的体积为V′= 2h= h3 , 由V=V′,得h= r.
8.解:(1)设所求的圆柱的底面半径为x,它的轴截面如图:BO=1,PO=3,圆柱的高为:h 由图得,,即h=3﹣3x. (2)S圆柱侧=2πhx=2π(3﹣3x)x=6π(x﹣x2),当x=时,函数取得最大值为:. ∴当圆柱的底面半径为时,它的侧面积最大为
9.解:如图所示,过C作CO1⊥AB于O1 , 在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R, ∴AC= R,BC=R,CO1= R,∴S球=4πR2 , =π× R× R= πR2 , =π× R×R= πR2 , ∴S几何体表=S球+ + = πR2 , ∴旋转所得到的几何体的表面积为 πR2 . 又V球= πR3 , = ?AO1?π?CO12= πR2?AO1 = BO1?πCO12= BO1?πR2∴V几何体=V球﹣( + )= πR3 .
