向心力教学课件
图片预览








文档简介
课件20张PPT。向心力[复习回顾]向心加速度的表达式?
[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r
向心加速度的方向如何?[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r
向心加速度的方向如何?
方向始终指向圆心
所以圆周运动中加速度a 肯定是变值第五章 曲线运动 第7节 向心力 做匀速圆周运动的物体受到的合外力总是指向圆心,这个力叫做向心力.
方向:沿半径指向圆心一、向心力的定义:公式:由an=rω2 , an=v2/r,F=ma得: Fn=mrω2或Fn=mv2/r
二、向心力的来源: 物体所受的合外力提供了物体做匀速圆周运动所需的向心力.说明:向心力不是物体除了重力、弹力、支持力等之外受到的力!它是从力的作用效果来命名的,可以是某个力或者某几个力的合力来提供的,所以在对物体进行受力分析时没有向心力的作用!
三、向心力的作用效果:只改变速度的方向,不改变速度的大小.
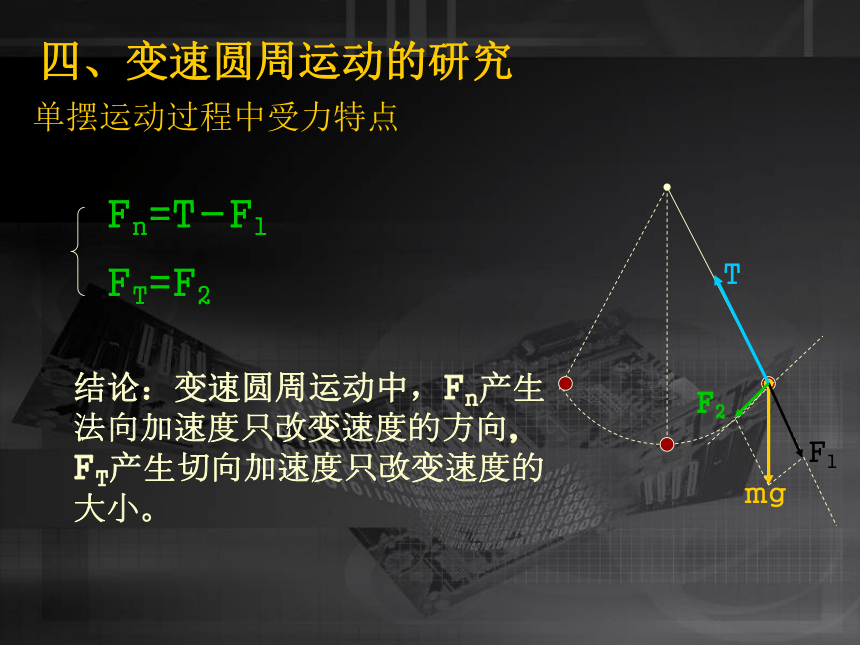
向心力指向圆心,而物体的运动方向沿圆周上该处的切线方向.两者相互垂直.所以在物体运动过程中向心力不做功不会引起物体动能的变化所以向心力不改变速度的大小.单摆运动过程中受力特点 mgTF1F2Fn=T-F1
FT=F2
结论:变速圆周运动中,Fn产生法向加速度只改变速度的方向,FT产生切向加速度只改变速度的大小。四、变速圆周运动的研究五、一般曲线运动的研究方法把曲线分割为许多极短的小段,每一小段看做一圆弧,然后研究质点经过曲线上某位置的运动时应用圆周运动的方法进行分析。注:曲线的弯曲程度不同,表示物体经过这些位置时的轨道半径不同。六、小结:
Fn=mrω2或Fn=mv2/r
在匀速圆周运动中,合外力提供了物体所需的向心力.向心力(或向心加速度)大小不变,方向始终指向圆心(不断地变化).
变速圆周圆周运动和一般曲线运动的研究方法练习分析实例1:
小球在光滑桌面上绕半径为r 的圆周做匀速圆周运动rv匀速圆周运动实例:实例1:
小球在光滑桌面上绕半径为r 的圆周做匀速圆周运动
rvFNmgT 绳子拉力T提供向心力匀速圆周运动实例:实例2匀速圆周运动实例:实例2mgfFNFN提供向心力匀速圆周运动实例:实例3匀速圆周运动实例:实例3mgFNf摩擦力f提供了向心力匀速圆周运动实例:实例4:
圆锥摆:rhθ 绳子拉力和重力的合力提供了向心力?如何验证
FN= mrω2是否等于F合?匀速圆周运动实例:实例5匀速圆周运动实例:实例5mgFN支持力与重力的合力提供向心力
[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r
向心加速度的方向如何?[复习回顾]向心加速度的表达式?
an=rω2 , an=v2/r
向心加速度的方向如何?
方向始终指向圆心
所以圆周运动中加速度a 肯定是变值第五章 曲线运动 第7节 向心力 做匀速圆周运动的物体受到的合外力总是指向圆心,这个力叫做向心力.
方向:沿半径指向圆心一、向心力的定义:公式:由an=rω2 , an=v2/r,F=ma得: Fn=mrω2或Fn=mv2/r
二、向心力的来源: 物体所受的合外力提供了物体做匀速圆周运动所需的向心力.说明:向心力不是物体除了重力、弹力、支持力等之外受到的力!它是从力的作用效果来命名的,可以是某个力或者某几个力的合力来提供的,所以在对物体进行受力分析时没有向心力的作用!
三、向心力的作用效果:只改变速度的方向,不改变速度的大小.
向心力指向圆心,而物体的运动方向沿圆周上该处的切线方向.两者相互垂直.所以在物体运动过程中向心力不做功不会引起物体动能的变化所以向心力不改变速度的大小.单摆运动过程中受力特点 mgTF1F2Fn=T-F1
FT=F2
结论:变速圆周运动中,Fn产生法向加速度只改变速度的方向,FT产生切向加速度只改变速度的大小。四、变速圆周运动的研究五、一般曲线运动的研究方法把曲线分割为许多极短的小段,每一小段看做一圆弧,然后研究质点经过曲线上某位置的运动时应用圆周运动的方法进行分析。注:曲线的弯曲程度不同,表示物体经过这些位置时的轨道半径不同。六、小结:
Fn=mrω2或Fn=mv2/r
在匀速圆周运动中,合外力提供了物体所需的向心力.向心力(或向心加速度)大小不变,方向始终指向圆心(不断地变化).
变速圆周圆周运动和一般曲线运动的研究方法练习分析实例1:
小球在光滑桌面上绕半径为r 的圆周做匀速圆周运动rv匀速圆周运动实例:实例1:
小球在光滑桌面上绕半径为r 的圆周做匀速圆周运动
rvFNmgT 绳子拉力T提供向心力匀速圆周运动实例:实例2匀速圆周运动实例:实例2mgfFNFN提供向心力匀速圆周运动实例:实例3匀速圆周运动实例:实例3mgFNf摩擦力f提供了向心力匀速圆周运动实例:实例4:
圆锥摆:rhθ 绳子拉力和重力的合力提供了向心力?如何验证
FN= mrω2是否等于F合?匀速圆周运动实例:实例5匀速圆周运动实例:实例5mgFN支持力与重力的合力提供向心力
