2018高中数学苏教版选修1-2练习:第2章推理与证明章末总结练习
文档属性
| 名称 | 2018高中数学苏教版选修1-2练习:第2章推理与证明章末总结练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 100.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 16:12:43 | ||
图片预览



文档简介
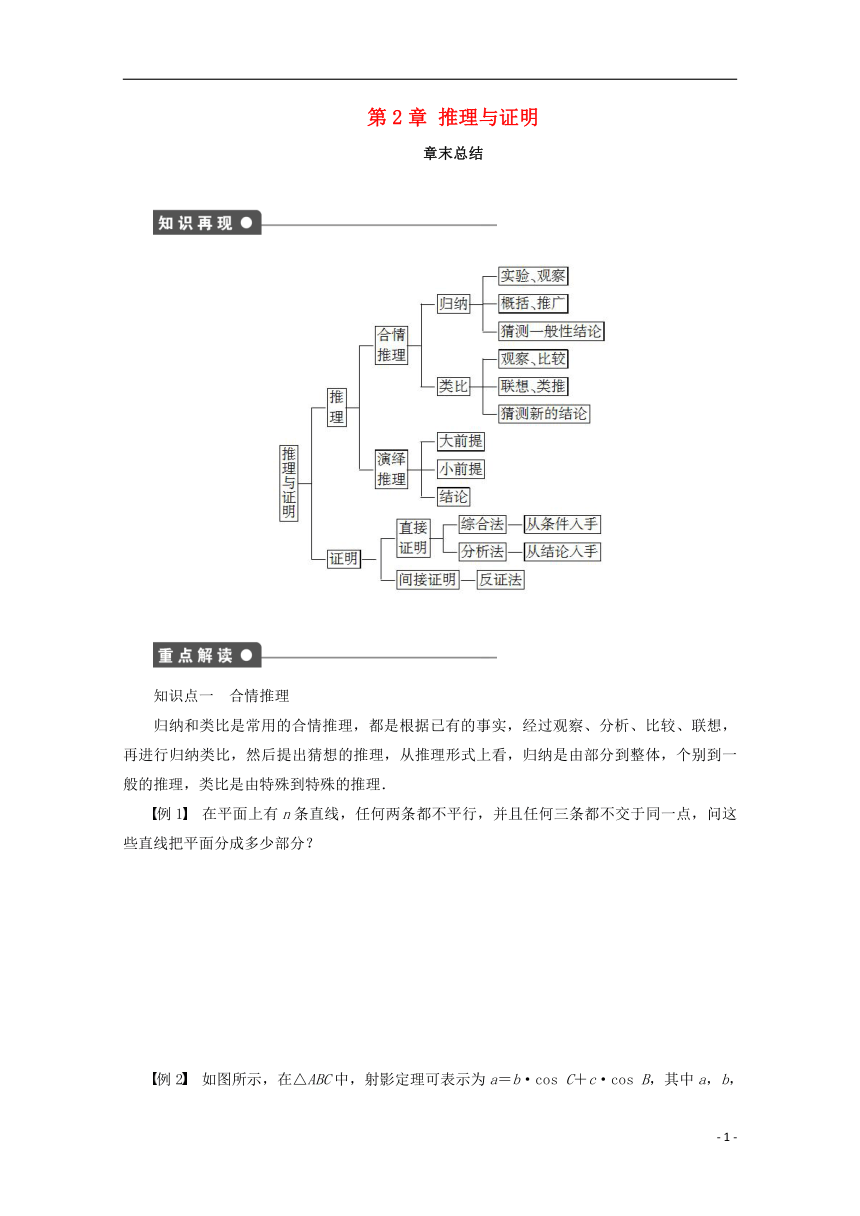
第2章 推理与证明
章末总结
知识点一 合情推理
归纳和类比是常用的合情推理,都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳类比,然后提出猜想的推理,从推理形式上看,归纳是由部分到整体,个别到一般的推理,类比是由特殊到特殊的推理.
例1 在平面上有n条直线,任何两条都不平行,并且任何三条都不交于同一点,问这些直线把平面分成多少部分?
例2 如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
知识点二 演绎推理
合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确.从二者在认识事物的过程中所发挥作用的角度考虑,它们又是紧密联系,相辅相成的.合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得,合情推理可以为演绎推理提供方向和思路.
演绎推理的一般模式是“三段论”.
例3 已知函数f(x)=+bx,其中a>0,b>0,x∈(0,+∞),确定f(x)的单调区间,并证明在每个单调区间上的增减性.
知识点三 综合法与分析法
综合法和分析法是直接证明中的两种最基本的证明方法,但两种证明方法思路截然相反,分析法既可用于寻找解题思路,也可以是完整的证明过程,分析法和综合法可相互转换,相互渗透,充分利用这一辩证关系,在解题中综合法和分析法联合运用,转换解题思路,增加解题途径.
例4 已知a,b,c均为正实数,且a+b+c=1,
求证:≥8.
知识点四 反证法
反证法是间接证明的一种基本方法,它不去直接证明结论,而是先否定结论,在否定结论的基础上,运用正确的推理,导出矛盾,从而肯定结论的真实性.在证明一些否定性命题、唯一性命题或含有“至多”、“至少”等字句的命题时,正面证明较难,可考虑反证法,即“正难则反”.
例5 已知a,b,c∈(0,1).求证:(1-a)b,(1-b)c,(1-c)a不可能都大于.
例6 如图所示,已知两直线l∩m=O,l?α,m?α,l?β,m?β,α∩β=a.求证:l与m中至少有一条与β相交.
章末总结
答案
重点解读
例1 解 设n条直线分平面为Sn部分,先实验观察特例有如下结果:
n
1
2
3
4
5
6
…
Sn
2
4
7
11
16
22
…
n与Sn之间的关系不太明显,但Sn-Sn-1有如下关系:
n
1
2
3
4
5
6
…
Sn
2
4
7
11
16
22
…
Sn-Sn-1
2
3
4
5
6
…
观察上表发现如下规律:Sn-Sn-1=n(n=2,3,…).
这是因为在n-1条直线后添加第n条直线被原(n-1)条直线截得的n段中的任何一段都将它所在的原平面一分为二,相应地增加n部分,
所以Sn=Sn-1+n,即Sn-Sn-1=n.
从而S2-S1=2,S3-S2=3,S4-S3=4,…,Sn-Sn-1=n.
将上面各式相加有Sn-S1=2+3+…+n,
∴Sn=S1+2+3+…+n=2+2+3+…+n
=1+.
例2 解
如图所示,在四面体P—ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.
我们猜想射影定理类比推理到三维空间,
其形式应为:
S=S1·cos α+S2·cos β+S3·cos γ.
例3 解 f(x)的单调区间为和,证明如下:设0f(x1)-f(x2)=-
=(x2-x1).
当0则x2-x1>0,0b,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在上是减函数.
当x2>x1≥时,
则x2-x1>0,x1x2>,∴f(x1)-f(x2)<0,即f(x1)∴f(x)在上是增函数.
例4 证明 方法一 (综合法)
=··
=··=
≥=8,
当且仅当a=b=c时等号成立,所以不等式成立.
方法二 (分析法)
要证≥8成立,
只需证··≥8成立.
因为a+b+c=1,
所以只需证··≥8成立.
即··≥8.
只需证··≥··≥8成立,
而··≥8显然成立,
故≥8成立.
例5 证明 假设三个式子同时大于,
即(1-a)b>,(1-b)c>,(1-c)a>,
三式相乘得:
(1-a)·a·(1-b)·b·(1-c)·c>, ①
又因为0∴0同理0所以(1-a)a·(1-b)b·(1-c)c≤, ②
①与②矛盾,所以假设不成立,故原命题成立.
例6 证明 假设l,m都不与β相交,
∵l?β,m?β,∴l∥β且m∥β.
又∵l?α,m?α,α∩β=a,
∴l∥a,m∥a,∴l∥m.
这与已知l、m是相交直线矛盾.
因此l和m至少有一条与β相交.
章末总结
知识点一 合情推理
归纳和类比是常用的合情推理,都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳类比,然后提出猜想的推理,从推理形式上看,归纳是由部分到整体,个别到一般的推理,类比是由特殊到特殊的推理.
例1 在平面上有n条直线,任何两条都不平行,并且任何三条都不交于同一点,问这些直线把平面分成多少部分?
例2 如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
知识点二 演绎推理
合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确.从二者在认识事物的过程中所发挥作用的角度考虑,它们又是紧密联系,相辅相成的.合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得,合情推理可以为演绎推理提供方向和思路.
演绎推理的一般模式是“三段论”.
例3 已知函数f(x)=+bx,其中a>0,b>0,x∈(0,+∞),确定f(x)的单调区间,并证明在每个单调区间上的增减性.
知识点三 综合法与分析法
综合法和分析法是直接证明中的两种最基本的证明方法,但两种证明方法思路截然相反,分析法既可用于寻找解题思路,也可以是完整的证明过程,分析法和综合法可相互转换,相互渗透,充分利用这一辩证关系,在解题中综合法和分析法联合运用,转换解题思路,增加解题途径.
例4 已知a,b,c均为正实数,且a+b+c=1,
求证:≥8.
知识点四 反证法
反证法是间接证明的一种基本方法,它不去直接证明结论,而是先否定结论,在否定结论的基础上,运用正确的推理,导出矛盾,从而肯定结论的真实性.在证明一些否定性命题、唯一性命题或含有“至多”、“至少”等字句的命题时,正面证明较难,可考虑反证法,即“正难则反”.
例5 已知a,b,c∈(0,1).求证:(1-a)b,(1-b)c,(1-c)a不可能都大于.
例6 如图所示,已知两直线l∩m=O,l?α,m?α,l?β,m?β,α∩β=a.求证:l与m中至少有一条与β相交.
章末总结
答案
重点解读
例1 解 设n条直线分平面为Sn部分,先实验观察特例有如下结果:
n
1
2
3
4
5
6
…
Sn
2
4
7
11
16
22
…
n与Sn之间的关系不太明显,但Sn-Sn-1有如下关系:
n
1
2
3
4
5
6
…
Sn
2
4
7
11
16
22
…
Sn-Sn-1
2
3
4
5
6
…
观察上表发现如下规律:Sn-Sn-1=n(n=2,3,…).
这是因为在n-1条直线后添加第n条直线被原(n-1)条直线截得的n段中的任何一段都将它所在的原平面一分为二,相应地增加n部分,
所以Sn=Sn-1+n,即Sn-Sn-1=n.
从而S2-S1=2,S3-S2=3,S4-S3=4,…,Sn-Sn-1=n.
将上面各式相加有Sn-S1=2+3+…+n,
∴Sn=S1+2+3+…+n=2+2+3+…+n
=1+.
例2 解
如图所示,在四面体P—ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.
我们猜想射影定理类比推理到三维空间,
其形式应为:
S=S1·cos α+S2·cos β+S3·cos γ.
例3 解 f(x)的单调区间为和,证明如下:设0
=(x2-x1).
当0
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在上是减函数.
当x2>x1≥时,
则x2-x1>0,x1x2>,
例4 证明 方法一 (综合法)
=··
=··=
≥=8,
当且仅当a=b=c时等号成立,所以不等式成立.
方法二 (分析法)
要证≥8成立,
只需证··≥8成立.
因为a+b+c=1,
所以只需证··≥8成立.
即··≥8.
只需证··≥··≥8成立,
而··≥8显然成立,
故≥8成立.
例5 证明 假设三个式子同时大于,
即(1-a)b>,(1-b)c>,(1-c)a>,
三式相乘得:
(1-a)·a·(1-b)·b·(1-c)·c>, ①
又因为0
①与②矛盾,所以假设不成立,故原命题成立.
例6 证明 假设l,m都不与β相交,
∵l?β,m?β,∴l∥β且m∥β.
又∵l?α,m?α,α∩β=a,
∴l∥a,m∥a,∴l∥m.
这与已知l、m是相交直线矛盾.
因此l和m至少有一条与β相交.
