2018高中数学苏教版选修1-2练习:第3章数系的扩充与复数的引入章末总结练习
文档属性
| 名称 | 2018高中数学苏教版选修1-2练习:第3章数系的扩充与复数的引入章末总结练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 16:14:41 | ||
图片预览

文档简介
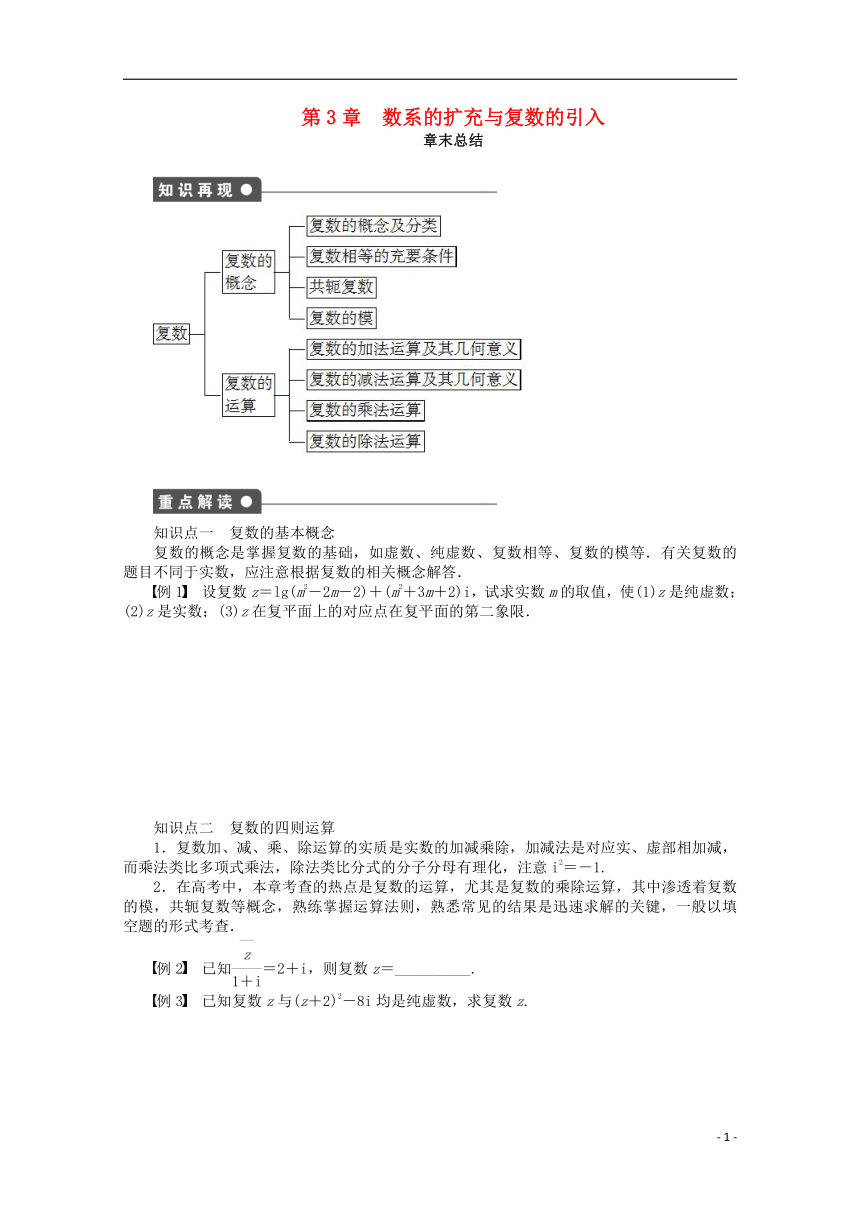
第3章 数系的扩充与复数的引入
章末总结
知识点一 复数的基本概念
复数的概念是掌握复数的基础,如虚数、纯虚数、复数相等、复数的模等.有关复数的题目不同于实数,应注意根据复数的相关概念解答.
例1 设复数z=lg(m2-2m-2)+(m2+3m+2)i,试求实数m的取值,使(1)z是纯虚数;(2)z是实数;(3)z在复平面上的对应点在复平面的第二象限.
知识点二 复数的四则运算
1.复数加、减、乘、除运算的实质是实数的加减乘除,加减法是对应实、虚部相加减,而乘法类比多项式乘法,除法类比分式的分子分母有理化,注意i2=-1.
2.在高考中,本章考查的热点是复数的运算,尤其是复数的乘除运算,其中渗透着复数的模,共轭复数等概念,熟练掌握运算法则,熟悉常见的结果是迅速求解的关键,一般以填空题的形式考查.
例2 已知=2+i,则复数z=__________.
例3 已知复数z与(z+2)2-8i均是纯虚数,求复数z.
知识点三 复数问题实数化
复数问题实数化是解决复数问题的最基本也是最重要的思想方法,桥梁是设z=x+yi (x,y∈R),依据是复数相等的充要条件.
例4 设存在复数z同时满足下列条件:
(1)复数z在复平面内对应的点位于第二象限;
(2)z·+2iz=8+ai (a∈R).求a的取值范围.
知识点四 复数的几何意义
1.复数的几何意义包括三个方面:复数的表示(点和向量)、复数的模的几何意义及复数的运算的几何意义.复数的几何意义体现了用几何图形的方法研究代数问题的数学思想方法.
2.复数的加减法的几何意义实质上是平行四边形法则和三角形法则.由减法的几何意义知|z-z1|表示复平面上两点Z与Z1之间的距离.
例5 在复平面内,向量对应的复数是2+i,向量对应的复数是-1-3i,则向量对应的复数为( )
A.1-2i B.-1+2i
C.3+4i D.-3-4i
例6 已知a∈R,z=(a2-2a+4)-(a2-2a+2)i所对应的点在第几象限?复数z对应的点的轨迹是什么?
章末总结
答案
重点解读
例1 解 (1)由得m=3.
∴当m=3时,z是纯虚数.
(2)由得m=-1或m=-2.
∴当m=-1或m=-2时,z是实数.
(3)由
得-1∴当-1例2 1-3i
解析 ∵=2+i,
∴=(2+i)(1+i)=2+3i-1=1+3i,
∴z=1-3i.
例3 解 设z=bi (b∈R,b≠0),
则(z+2)2-8i=(2+bi)2-8i=(4-b2)+(4b-8)i,
∵(z+2)2-8i为纯虚数,∴4-b2=0且4b-8≠0.
∴b=-2.∴z=-2i.
例4 解 设z=x+yi (x,y∈R),则=x-yi.
由(1)知,x<0,y>0,
又z·+2iz=8+ai (a∈R),
故(x+yi)(x-yi)+2i(x+yi)=8+ai,
即(x2+y2-2y)+2xi=8+ai.
∴
消去x,整理,得4(y-1)2=36-a2,
∵4(y-1)2≥0,∴36-a2≥0,∴-6≤a≤6.
又2x=a,而x<0,∴a<0,∴-6≤a<0.
所以a的取值范围为[-6,0).
例5 D [∵对应复数2+i,对应复数1+3i,
∴对应复数(2+i)+(1+3i)=3+4i,
∴对应的复数是-3-4i.]
例6 解 由a2-2a+4=(a-1)2+3≥3,
-(a2-2a+2)=-(a-1)2-1≤-1,
∴复数z的实部为正数,虚部为负数,因此,复数z的对应点在第四象限.
设z=x+yi (x、y∈R),
则
消去a2-2a得:y=-x+2 (x≥3).
∴复数z的对应点的轨迹是一条射线,
方程为y=-x+2 (x≥3).
章末总结
知识点一 复数的基本概念
复数的概念是掌握复数的基础,如虚数、纯虚数、复数相等、复数的模等.有关复数的题目不同于实数,应注意根据复数的相关概念解答.
例1 设复数z=lg(m2-2m-2)+(m2+3m+2)i,试求实数m的取值,使(1)z是纯虚数;(2)z是实数;(3)z在复平面上的对应点在复平面的第二象限.
知识点二 复数的四则运算
1.复数加、减、乘、除运算的实质是实数的加减乘除,加减法是对应实、虚部相加减,而乘法类比多项式乘法,除法类比分式的分子分母有理化,注意i2=-1.
2.在高考中,本章考查的热点是复数的运算,尤其是复数的乘除运算,其中渗透着复数的模,共轭复数等概念,熟练掌握运算法则,熟悉常见的结果是迅速求解的关键,一般以填空题的形式考查.
例2 已知=2+i,则复数z=__________.
例3 已知复数z与(z+2)2-8i均是纯虚数,求复数z.
知识点三 复数问题实数化
复数问题实数化是解决复数问题的最基本也是最重要的思想方法,桥梁是设z=x+yi (x,y∈R),依据是复数相等的充要条件.
例4 设存在复数z同时满足下列条件:
(1)复数z在复平面内对应的点位于第二象限;
(2)z·+2iz=8+ai (a∈R).求a的取值范围.
知识点四 复数的几何意义
1.复数的几何意义包括三个方面:复数的表示(点和向量)、复数的模的几何意义及复数的运算的几何意义.复数的几何意义体现了用几何图形的方法研究代数问题的数学思想方法.
2.复数的加减法的几何意义实质上是平行四边形法则和三角形法则.由减法的几何意义知|z-z1|表示复平面上两点Z与Z1之间的距离.
例5 在复平面内,向量对应的复数是2+i,向量对应的复数是-1-3i,则向量对应的复数为( )
A.1-2i B.-1+2i
C.3+4i D.-3-4i
例6 已知a∈R,z=(a2-2a+4)-(a2-2a+2)i所对应的点在第几象限?复数z对应的点的轨迹是什么?
章末总结
答案
重点解读
例1 解 (1)由得m=3.
∴当m=3时,z是纯虚数.
(2)由得m=-1或m=-2.
∴当m=-1或m=-2时,z是实数.
(3)由
得-1
解析 ∵=2+i,
∴=(2+i)(1+i)=2+3i-1=1+3i,
∴z=1-3i.
例3 解 设z=bi (b∈R,b≠0),
则(z+2)2-8i=(2+bi)2-8i=(4-b2)+(4b-8)i,
∵(z+2)2-8i为纯虚数,∴4-b2=0且4b-8≠0.
∴b=-2.∴z=-2i.
例4 解 设z=x+yi (x,y∈R),则=x-yi.
由(1)知,x<0,y>0,
又z·+2iz=8+ai (a∈R),
故(x+yi)(x-yi)+2i(x+yi)=8+ai,
即(x2+y2-2y)+2xi=8+ai.
∴
消去x,整理,得4(y-1)2=36-a2,
∵4(y-1)2≥0,∴36-a2≥0,∴-6≤a≤6.
又2x=a,而x<0,∴a<0,∴-6≤a<0.
所以a的取值范围为[-6,0).
例5 D [∵对应复数2+i,对应复数1+3i,
∴对应复数(2+i)+(1+3i)=3+4i,
∴对应的复数是-3-4i.]
例6 解 由a2-2a+4=(a-1)2+3≥3,
-(a2-2a+2)=-(a-1)2-1≤-1,
∴复数z的实部为正数,虚部为负数,因此,复数z的对应点在第四象限.
设z=x+yi (x、y∈R),
则
消去a2-2a得:y=-x+2 (x≥3).
∴复数z的对应点的轨迹是一条射线,
方程为y=-x+2 (x≥3).
