2018高中数学苏教版选修1-2练习:第4章框图模块综合检测(B)
文档属性
| 名称 | 2018高中数学苏教版选修1-2练习:第4章框图模块综合检测(B) |  | |
| 格式 | zip | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 16:15:37 | ||
图片预览


文档简介
第4章 框图
模块综合检测(B)
(时间:120分钟 满分:160分)
一、填空题(本大题共14小题,每小题5分,共70分)
1.下列说法错误的是________.
①球的体积与它的半径具有相关关系
②在回归分析中χ2的值越大,说明拟合效果越好
③在独立性检验中,χ2的值越大,说明确定两个量有关系的把握越大
2.如果执行如图所示的框图,输入N=5,则输出的数等于________.
3.已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则=2”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等”,则=______.
4.若z=x+yi (x,y∈R)是方程z2=-3+4i的一个根,则z等于______________.
5.设a,b,c,d∈R,若为实数,则bc+ad=______.
6.由①正方形的四个内角相等;②矩形的四个内角相等;③正方形是矩形,根据“三段论”推理出一个结论,则作为大前提、小前提、结论的分别为________.
7.若复数z满足|z|-=,则z=__________.
8.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是____________.
9.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来断言“X和Y有无关系”.如果χ2>5.024,那么就有把握认为“X和Y有关系”的百分比为________.
10.下面给出了关于复数的四种类比推理,
①复数的加减法运算,可以类比多项式的加减法运算法则.
②由向量a的性质|a|2=a2,可以类比得到复数z的性质:|z|2=z2.
③方程ax2+bx+c=0 (a,b,c∈R)有两个不同实根的条件是b2-4ac>0,类比可得方程ax2+bx+c=0 (a、b、c∈C)有两个不同复数根的条件是b2-4ac>0.
④由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是________.
11.设复数z1=2-i,z2=1-3i,则复数+的虚部为________.
12.由1,,,,,…归纳猜测第n项为________.
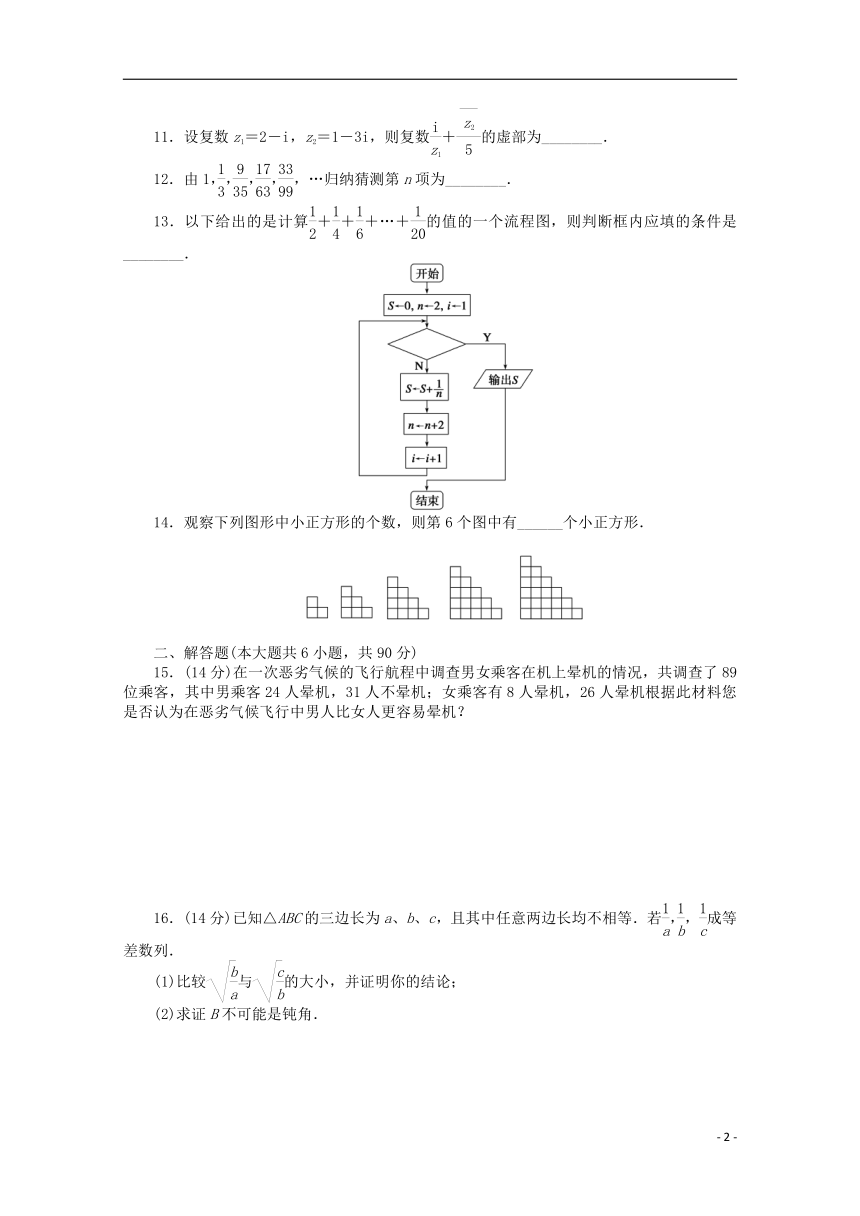
13.以下给出的是计算+++…+的值的一个流程图,则判断框内应填的条件是________.
14.观察下列图形中小正方形的个数,则第6个图中有______个小正方形.
二、解答题(本大题共6小题,共90分)
15.(14分)在一次恶劣气候的飞行航程中调查男女乘客在机上晕机的情况,共调查了89位乘客,其中男乘客24人晕机,31人不晕机;女乘客有8人晕机,26人晕机根据此材料您是否认为在恶劣气候飞行中男人比女人更容易晕机?
16.(14分)已知△ABC的三边长为a、b、c,且其中任意两边长均不相等.若,,成等差数列.
(1)比较与的大小,并证明你的结论;
(2)求证B不可能是钝角.
17.(14分)已知复数z满足|z|2+(z+)i=(i为虚数单位),求z.
18.(16分)求证:函数f(x)=是奇函数,且在定义域上是增函数.
19.(16分)设计一个框图,表示平面向量的知识结构.
20.(16分)已知函数f(x)=tan x,x∈,若x1,x2∈,且x1≠x2,
求证:[f(x1)+f(x2)]>f.
(注:tan =)
模块综合检测(B)
答案
1.①
解析 球的体积与半径的关系是确定的,是函数关系.
2.
解析 第一次运行N=5,k=1,S=0,S=0+,
1<5成立,进入第二次运行;k=2,S=+,
2<5成立,进入第三次运行;k=3,S=++,3<5成立,进入第四次运行;k=4,S=+++,4<5成立,进入第五次运行;k=5,S=++++=1-=,5<5不成立,
此时退出循环,输出S.
3.3
解析
如图设正四面体的棱长为1,则易知其高AM=,此时易知点O即为正四面体内切球的球心,设其半径为r,利用等积法有4××r=××?r=,
故AO=AM-MO=-=,故==3.
4.-1-2i或1+2i
解析 z2=x2-y2+2xyi
∴,∴或.
∴z=-1-2i或z=1+2i.
5.0
解析 ∵=
=是实数,
∴cb+ad=0.
6.②③①
解析 根据三段论的一般形式,可以得到大前提是②,小前提是③,结论是①.
7.3+4i
解析 ∵|z|-===2+4i.
∴|z|=+2+4i∈R,∴设z=a+4i (a∈R),
∴=a+2, 解得a=3,∴z=3+4i.
8.归纳推理 9.97.5% 10.①④
11.1
解析 +=+=+=i.
∴+的虚部等于1.
12.
解析 各数可以写成:,,,,,…,不难得出:分子是2n+1,分母为(2n-1)·(2n+1).所以an=.
13.i>10
解析 所求和式为10项的和,该算法程序中用循环变量i来控制循环次数,显然当i>10时,循环结束,并输出和S,故判断条件应为i>10.
14.28
解析 第一个图为3个正方形,第二个图为3+3=6个正方形,第三个图为6+4=10个正方形,第四个图为10+5=15个正方形,第五个图为15+6=21个正方形,因此可推测第六个图为21+7=28个正方形.
15.解 由已知数据制成下表:
晕机
不晕机
合计
男人
24
31
55
女人
8
26
34
合计
32
57
89
由χ2=
=≈3.689>2.706.
我们有90%的把握认为在本次飞机飞行中,晕机与男女有关.尽管这次航班中男人晕机的比例比女人晕机的比例高,但我们不能认为在恶劣气候飞行中男人比女人更容易晕机.
16.(1)解 大小关系为<,证明如下:
要证<,只需证<,
∵a、b、c>0,只需证:b2∵,,成等差数列,
∴=+≥2,
∴b2≤ac,又a、b、c任意两边均不相等,
∴b2故所得大小关系正确.
(2)证明 假设B是钝角,则cos B<0,
而cos B=≥>>0.
这与cos B<0矛盾,故假设不成立.
∴B不可能是钝角.
17.解 由已知得|z|2+(z+)i=1-i,
设z=x+yi (x,y∈R),代入上式得
x2+y2+2xi=1-i,∴,
解得,∴z=-±i.
18.证明 f(x)==1-定义域x∈R.
f(x)+f(-x)=2-
=2-=2-2=0.
∴f(-x)=-f(x),∴f(x)为奇函数.
任取x1,x2∈R且x1f(x1)-f(x2)=-
=2=2·
∵x1∴f(x1)19.解
20.证明 要证[f(x1)+f(x2)]>f,
即证明(tan x1+tan x2)>tan,
只需证明>tan ,
只需证明>.
由于x1、x2∈,故x1+x2∈(0,π).
∴cos x1cos x2>0,sin(x1+x2)>0,
1+cos(x1+x2)>0,
故只需证明1+cos(x1+x2)>2cos x1cos x2,
即证1+cos x1cos x2-sin x1sin x2>2cos x1cos x2,
即证:cos(x1-x2)<1.
这由x1、x2∈,x1≠x2知上式是显然成立的.因此,[f(x1)+f(x2)]>f.
模块综合检测(B)
(时间:120分钟 满分:160分)
一、填空题(本大题共14小题,每小题5分,共70分)
1.下列说法错误的是________.
①球的体积与它的半径具有相关关系
②在回归分析中χ2的值越大,说明拟合效果越好
③在独立性检验中,χ2的值越大,说明确定两个量有关系的把握越大
2.如果执行如图所示的框图,输入N=5,则输出的数等于________.
3.已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则=2”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等”,则=______.
4.若z=x+yi (x,y∈R)是方程z2=-3+4i的一个根,则z等于______________.
5.设a,b,c,d∈R,若为实数,则bc+ad=______.
6.由①正方形的四个内角相等;②矩形的四个内角相等;③正方形是矩形,根据“三段论”推理出一个结论,则作为大前提、小前提、结论的分别为________.
7.若复数z满足|z|-=,则z=__________.
8.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是____________.
9.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来断言“X和Y有无关系”.如果χ2>5.024,那么就有把握认为“X和Y有关系”的百分比为________.
10.下面给出了关于复数的四种类比推理,
①复数的加减法运算,可以类比多项式的加减法运算法则.
②由向量a的性质|a|2=a2,可以类比得到复数z的性质:|z|2=z2.
③方程ax2+bx+c=0 (a,b,c∈R)有两个不同实根的条件是b2-4ac>0,类比可得方程ax2+bx+c=0 (a、b、c∈C)有两个不同复数根的条件是b2-4ac>0.
④由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是________.
11.设复数z1=2-i,z2=1-3i,则复数+的虚部为________.
12.由1,,,,,…归纳猜测第n项为________.
13.以下给出的是计算+++…+的值的一个流程图,则判断框内应填的条件是________.
14.观察下列图形中小正方形的个数,则第6个图中有______个小正方形.
二、解答题(本大题共6小题,共90分)
15.(14分)在一次恶劣气候的飞行航程中调查男女乘客在机上晕机的情况,共调查了89位乘客,其中男乘客24人晕机,31人不晕机;女乘客有8人晕机,26人晕机根据此材料您是否认为在恶劣气候飞行中男人比女人更容易晕机?
16.(14分)已知△ABC的三边长为a、b、c,且其中任意两边长均不相等.若,,成等差数列.
(1)比较与的大小,并证明你的结论;
(2)求证B不可能是钝角.
17.(14分)已知复数z满足|z|2+(z+)i=(i为虚数单位),求z.
18.(16分)求证:函数f(x)=是奇函数,且在定义域上是增函数.
19.(16分)设计一个框图,表示平面向量的知识结构.
20.(16分)已知函数f(x)=tan x,x∈,若x1,x2∈,且x1≠x2,
求证:[f(x1)+f(x2)]>f.
(注:tan =)
模块综合检测(B)
答案
1.①
解析 球的体积与半径的关系是确定的,是函数关系.
2.
解析 第一次运行N=5,k=1,S=0,S=0+,
1<5成立,进入第二次运行;k=2,S=+,
2<5成立,进入第三次运行;k=3,S=++,3<5成立,进入第四次运行;k=4,S=+++,4<5成立,进入第五次运行;k=5,S=++++=1-=,5<5不成立,
此时退出循环,输出S.
3.3
解析
如图设正四面体的棱长为1,则易知其高AM=,此时易知点O即为正四面体内切球的球心,设其半径为r,利用等积法有4××r=××?r=,
故AO=AM-MO=-=,故==3.
4.-1-2i或1+2i
解析 z2=x2-y2+2xyi
∴,∴或.
∴z=-1-2i或z=1+2i.
5.0
解析 ∵=
=是实数,
∴cb+ad=0.
6.②③①
解析 根据三段论的一般形式,可以得到大前提是②,小前提是③,结论是①.
7.3+4i
解析 ∵|z|-===2+4i.
∴|z|=+2+4i∈R,∴设z=a+4i (a∈R),
∴=a+2, 解得a=3,∴z=3+4i.
8.归纳推理 9.97.5% 10.①④
11.1
解析 +=+=+=i.
∴+的虚部等于1.
12.
解析 各数可以写成:,,,,,…,不难得出:分子是2n+1,分母为(2n-1)·(2n+1).所以an=.
13.i>10
解析 所求和式为10项的和,该算法程序中用循环变量i来控制循环次数,显然当i>10时,循环结束,并输出和S,故判断条件应为i>10.
14.28
解析 第一个图为3个正方形,第二个图为3+3=6个正方形,第三个图为6+4=10个正方形,第四个图为10+5=15个正方形,第五个图为15+6=21个正方形,因此可推测第六个图为21+7=28个正方形.
15.解 由已知数据制成下表:
晕机
不晕机
合计
男人
24
31
55
女人
8
26
34
合计
32
57
89
由χ2=
=≈3.689>2.706.
我们有90%的把握认为在本次飞机飞行中,晕机与男女有关.尽管这次航班中男人晕机的比例比女人晕机的比例高,但我们不能认为在恶劣气候飞行中男人比女人更容易晕机.
16.(1)解 大小关系为<,证明如下:
要证<,只需证<,
∵a、b、c>0,只需证:b2
∴=+≥2,
∴b2≤ac,又a、b、c任意两边均不相等,
∴b2
(2)证明 假设B是钝角,则cos B<0,
而cos B=≥>>0.
这与cos B<0矛盾,故假设不成立.
∴B不可能是钝角.
17.解 由已知得|z|2+(z+)i=1-i,
设z=x+yi (x,y∈R),代入上式得
x2+y2+2xi=1-i,∴,
解得,∴z=-±i.
18.证明 f(x)==1-定义域x∈R.
f(x)+f(-x)=2-
=2-=2-2=0.
∴f(-x)=-f(x),∴f(x)为奇函数.
任取x1,x2∈R且x1
=2=2·
∵x1
20.证明 要证[f(x1)+f(x2)]>f,
即证明(tan x1+tan x2)>tan,
只需证明>tan ,
只需证明>.
由于x1、x2∈,故x1+x2∈(0,π).
∴cos x1cos x2>0,sin(x1+x2)>0,
1+cos(x1+x2)>0,
故只需证明1+cos(x1+x2)>2cos x1cos x2,
即证1+cos x1cos x2-sin x1sin x2>2cos x1cos x2,
即证:cos(x1-x2)<1.
这由x1、x2∈,x1≠x2知上式是显然成立的.因此,[f(x1)+f(x2)]>f.
