2018高中数学苏教版选修1-2练习:第4章框图模块综合检测(C)
文档属性
| 名称 | 2018高中数学苏教版选修1-2练习:第4章框图模块综合检测(C) |
|
|
| 格式 | zip | ||
| 文件大小 | 113.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 16:15:48 | ||
图片预览


文档简介
第4章 框图
模块综合检测(C)
(时间:120分钟 满分:160分)
一、填空题(本大题共14小题,每小题5分,共70分)
1.复数z1=3-i,z2=1-i,则z1·z2在复平面内的对应点位于第______象限.
2.复数z1=2-i,z2=-2i,则z1+z2等于________.
3.向量对应的复数是5-4i,向量对应的复数是-5+4i,则+对应的复数是________.
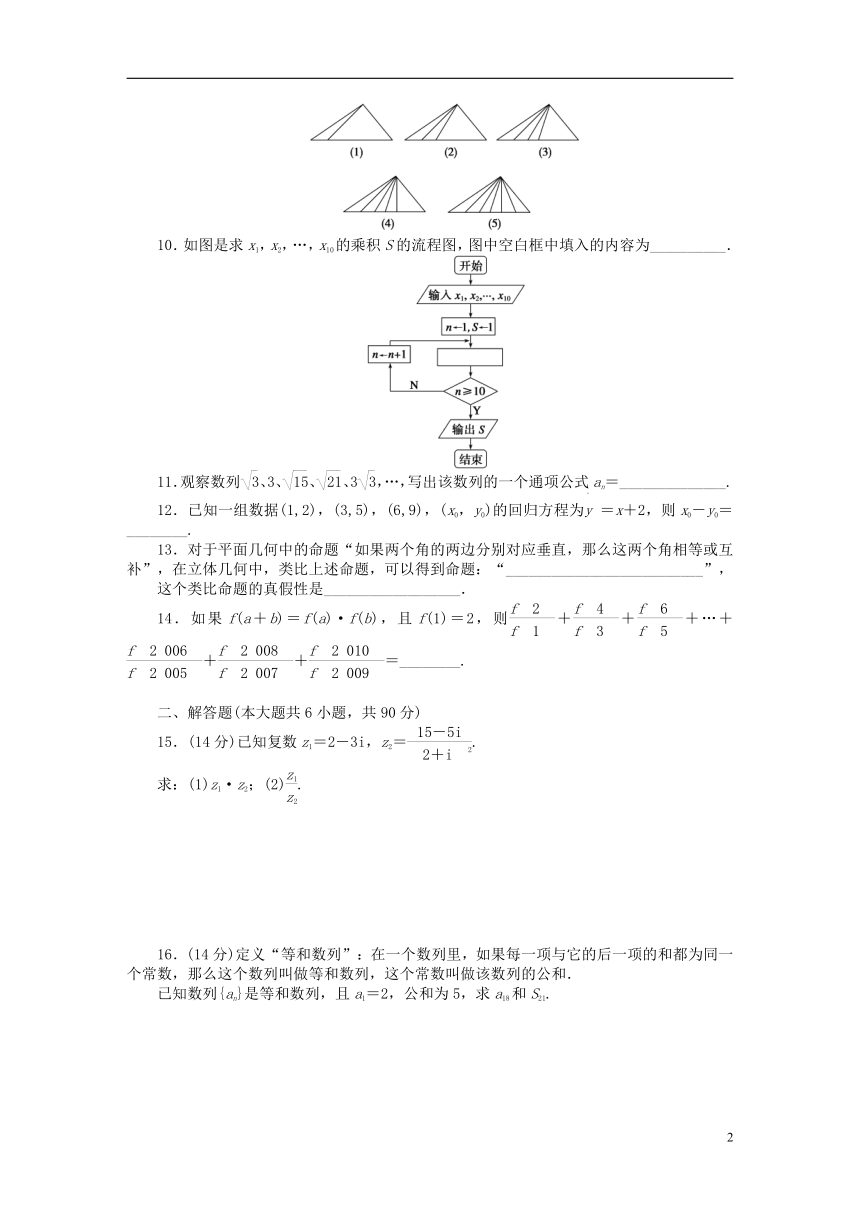
4.将x=2 011输入下面流程图得结果为________.
5.下面使用类比推理正确的是________.
①“若a·3=b·3,则a=b”类推出“若a·0=b·0,则a=b”;
②“若(a+b)c=ac+bc”类推出“(a·b)c=ac·bc”;
③“若(a+b)c=ac+bc”类推出“=+ (c≠0)”;
④“(ab)n=anbn”类推出“(a+b)n=an+bn”.
6.下列结构图中表示从属关系的是( )
①→→→
②—
③—
④―→―→
7.在图中所示的结构图中,“等差数列”与“等比数列”的上位要素是________.
8.我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有________.
①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱锥.
9.根据下列各图中三角形的个数,推断第20个图中三角形的个数是________.
10.如图是求x1,x2,…,x10的乘积S的流程图,图中空白框中填入的内容为__________.
11.观察数列、3、、、3,…,写出该数列的一个通项公式an=______________.
12.已知一组数据(1,2),(3,5),(6,9),(x0,y0)的回归方程为 =x+2,则x0-y0=________.
13.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题,可以得到命题:“__________________________”,
这个类比命题的真假性是__________________.
14.如果f(a+b)=f(a)·f(b),且f(1)=2,则+++…+++=________.
二、解答题(本大题共6小题,共90分)
15.(14分)已知复数z1=2-3i,z2=.
求:(1)z1·z2;(2).
16.(14分)定义“等和数列”:在一个数列里,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.
已知数列{an}是等和数列,且a1=2,公和为5,求a18和S21.
17.(14分)设a>0,b>0,a+b=1,求证:++≥8.
18.(16分)在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1
2
3
4
5
价格x
1.4
1.6
1.8
2
2.2
需求量y
12
10
7
5
3
已知xiyi=62,x=16.6.
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
19.(16分)某保险公司业务流程如下:(1)保户投保、填单交费、公司承保、出具保单;(2)保户提赔,公司勘查;同意,则赔偿,否则拒赔.画出该公司的业务流程图.
20.(16分)已知关于x的方程x2+zx+4+3i=0有实数根,求复数z的模的最小值.
模块综合检测(C)
答案
1.四
解析 z1·z2=(3-i)(1-i)=2-4i,对应点在第四象限.
2.-i
解析 z1+z2=-i=-i.
3.0
解析 +=5-4i+(-5+4i)=0.
4.2 012
解析 框图中的函数为y=
∴当x=2 011时,y=2 012.
5.③
解析 对于①,a=1,b=2也可以;对于②,当a=2,b=3,c=4时推理不正确;对于④,一般情况下(a+b)n≠an+bn.
6.③ 7.数列
8.①③
解析 ①③属于相似体.
9.231
解析 (1)中有3个,(2)中有6个,(3)中有10个,(4)中有15个,(5)中有21个.设它们的个数依次为a1=3,a2=6,a3=10,a4=15,a5=21.则有a2-a1=3,a3-a2=4,a4-a3=5,a5-a4=6.
猜测a20-a19=20+1=21.
则a20=a1+(a2-a1)+(a3-a2)+…+(a20-a19)=3+3+4+5+…+21=3+
=231.
10.S←S*xn
解析 由题意,输出的是10个数的乘积,因此处理框中应是分别计算这10个数相乘,
∴循环体应为S=S*xn.
11. (n∈N*)
解析 ∵a1=,a2=3=,
a3==,a4==,
a5=3=.
∴猜想an= (n∈N*).
12.-2
解析 ∵==,
==,
∵ =x+2恒过定点(,),
∴=+2,∴x0-y0=-2.
13.如果两个二面角的两个半平面分别对应垂直,那么这两个二面角相等或互补 假命题
14.2 010
解析 令a=n,b=1,则f(n+1)=f(n)·f(1),
∴=f(1)=2,
∴++…++
=2×1 005=2 010.
15.解 z2==1-3i.
(1)z1·z2=(2-3i)(1-3i)=-7-9i.
(2)==+i.
16.解 由“等和数列”的定义有:
a1+a2=a2+a3=a3+a4=…=5,
得a1=a3=a5=…=a2n-1=2,
a2=a4=a6=…=a2n=3,所以a18=3,
S21=(a1+a2)+(a3+a4)+…+(a19+a20)+a21
=5×10+2=52.
17.证明 方法一 综合法
∵a>0,b>0,a+b=1,
∴1=a+b≥2,≤,ab≤,∴≥4,
又+=(a+b)=2++≥4,
∴++≥8(当且仅当a=b=时等号成立).
方法二 分析法
∵a>0,b>0,a+b=1,要证++≥8,
只要证+≥8,
只要证+≥8,
即证+≥4,
也就是证+≥4,
即证+≥2.
由基本不等式可知,当a>0,b>0时,+≥2成立,所以原不等式成立.
18.解 (1)散点图如图所示:
(2)因为=×9=1.8,=×37=7.4,
xiyi=62,x=16.6,
所以 ==
=-11.5,
=- =7.4+11.5×1.8=28.1,
故y对x的线性回归方程为 =28.1-11.5x.
(3) =28.1-11.5×1.9=6.25(t).
19.解 业务流程图如下:
20. 解 设x=a∈R为已知方程的实根,
则a2+az+4+3i=0.
又a=0不满足此方程,∴z=-.
|z|2=2+2=
=a2++8≥2+8=18.
即|z|≥3,当且仅当a2=,即a=±时等号成立.
∴a=±时,|z|取最小值是3.
模块综合检测(C)
(时间:120分钟 满分:160分)
一、填空题(本大题共14小题,每小题5分,共70分)
1.复数z1=3-i,z2=1-i,则z1·z2在复平面内的对应点位于第______象限.
2.复数z1=2-i,z2=-2i,则z1+z2等于________.
3.向量对应的复数是5-4i,向量对应的复数是-5+4i,则+对应的复数是________.
4.将x=2 011输入下面流程图得结果为________.
5.下面使用类比推理正确的是________.
①“若a·3=b·3,则a=b”类推出“若a·0=b·0,则a=b”;
②“若(a+b)c=ac+bc”类推出“(a·b)c=ac·bc”;
③“若(a+b)c=ac+bc”类推出“=+ (c≠0)”;
④“(ab)n=anbn”类推出“(a+b)n=an+bn”.
6.下列结构图中表示从属关系的是( )
①→→→
②—
③—
④―→―→
7.在图中所示的结构图中,“等差数列”与“等比数列”的上位要素是________.
8.我们把平面几何里相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.下列几何体中,一定属于相似体的有________.
①两个球体;②两个长方体;③两个正四面体;④两个正三棱柱;⑤两个正四棱锥.
9.根据下列各图中三角形的个数,推断第20个图中三角形的个数是________.
10.如图是求x1,x2,…,x10的乘积S的流程图,图中空白框中填入的内容为__________.
11.观察数列、3、、、3,…,写出该数列的一个通项公式an=______________.
12.已知一组数据(1,2),(3,5),(6,9),(x0,y0)的回归方程为 =x+2,则x0-y0=________.
13.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题,可以得到命题:“__________________________”,
这个类比命题的真假性是__________________.
14.如果f(a+b)=f(a)·f(b),且f(1)=2,则+++…+++=________.
二、解答题(本大题共6小题,共90分)
15.(14分)已知复数z1=2-3i,z2=.
求:(1)z1·z2;(2).
16.(14分)定义“等和数列”:在一个数列里,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.
已知数列{an}是等和数列,且a1=2,公和为5,求a18和S21.
17.(14分)设a>0,b>0,a+b=1,求证:++≥8.
18.(16分)在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1
2
3
4
5
价格x
1.4
1.6
1.8
2
2.2
需求量y
12
10
7
5
3
已知xiyi=62,x=16.6.
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
19.(16分)某保险公司业务流程如下:(1)保户投保、填单交费、公司承保、出具保单;(2)保户提赔,公司勘查;同意,则赔偿,否则拒赔.画出该公司的业务流程图.
20.(16分)已知关于x的方程x2+zx+4+3i=0有实数根,求复数z的模的最小值.
模块综合检测(C)
答案
1.四
解析 z1·z2=(3-i)(1-i)=2-4i,对应点在第四象限.
2.-i
解析 z1+z2=-i=-i.
3.0
解析 +=5-4i+(-5+4i)=0.
4.2 012
解析 框图中的函数为y=
∴当x=2 011时,y=2 012.
5.③
解析 对于①,a=1,b=2也可以;对于②,当a=2,b=3,c=4时推理不正确;对于④,一般情况下(a+b)n≠an+bn.
6.③ 7.数列
8.①③
解析 ①③属于相似体.
9.231
解析 (1)中有3个,(2)中有6个,(3)中有10个,(4)中有15个,(5)中有21个.设它们的个数依次为a1=3,a2=6,a3=10,a4=15,a5=21.则有a2-a1=3,a3-a2=4,a4-a3=5,a5-a4=6.
猜测a20-a19=20+1=21.
则a20=a1+(a2-a1)+(a3-a2)+…+(a20-a19)=3+3+4+5+…+21=3+
=231.
10.S←S*xn
解析 由题意,输出的是10个数的乘积,因此处理框中应是分别计算这10个数相乘,
∴循环体应为S=S*xn.
11. (n∈N*)
解析 ∵a1=,a2=3=,
a3==,a4==,
a5=3=.
∴猜想an= (n∈N*).
12.-2
解析 ∵==,
==,
∵ =x+2恒过定点(,),
∴=+2,∴x0-y0=-2.
13.如果两个二面角的两个半平面分别对应垂直,那么这两个二面角相等或互补 假命题
14.2 010
解析 令a=n,b=1,则f(n+1)=f(n)·f(1),
∴=f(1)=2,
∴++…++
=2×1 005=2 010.
15.解 z2==1-3i.
(1)z1·z2=(2-3i)(1-3i)=-7-9i.
(2)==+i.
16.解 由“等和数列”的定义有:
a1+a2=a2+a3=a3+a4=…=5,
得a1=a3=a5=…=a2n-1=2,
a2=a4=a6=…=a2n=3,所以a18=3,
S21=(a1+a2)+(a3+a4)+…+(a19+a20)+a21
=5×10+2=52.
17.证明 方法一 综合法
∵a>0,b>0,a+b=1,
∴1=a+b≥2,≤,ab≤,∴≥4,
又+=(a+b)=2++≥4,
∴++≥8(当且仅当a=b=时等号成立).
方法二 分析法
∵a>0,b>0,a+b=1,要证++≥8,
只要证+≥8,
只要证+≥8,
即证+≥4,
也就是证+≥4,
即证+≥2.
由基本不等式可知,当a>0,b>0时,+≥2成立,所以原不等式成立.
18.解 (1)散点图如图所示:
(2)因为=×9=1.8,=×37=7.4,
xiyi=62,x=16.6,
所以 ==
=-11.5,
=- =7.4+11.5×1.8=28.1,
故y对x的线性回归方程为 =28.1-11.5x.
(3) =28.1-11.5×1.9=6.25(t).
19.解 业务流程图如下:
20. 解 设x=a∈R为已知方程的实根,
则a2+az+4+3i=0.
又a=0不满足此方程,∴z=-.
|z|2=2+2=
=a2++8≥2+8=18.
即|z|≥3,当且仅当a2=,即a=±时等号成立.
∴a=±时,|z|取最小值是3.
