23.2 解直角三角形及其应用课时作业(2)
文档属性
| 名称 | 23.2 解直角三角形及其应用课时作业(2) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-01 00:00:00 | ||
图片预览





文档简介
23.2 解直角三角形及其应用课时作业(2)
姓名:__________班级:__________考号:__________
一 、选择题
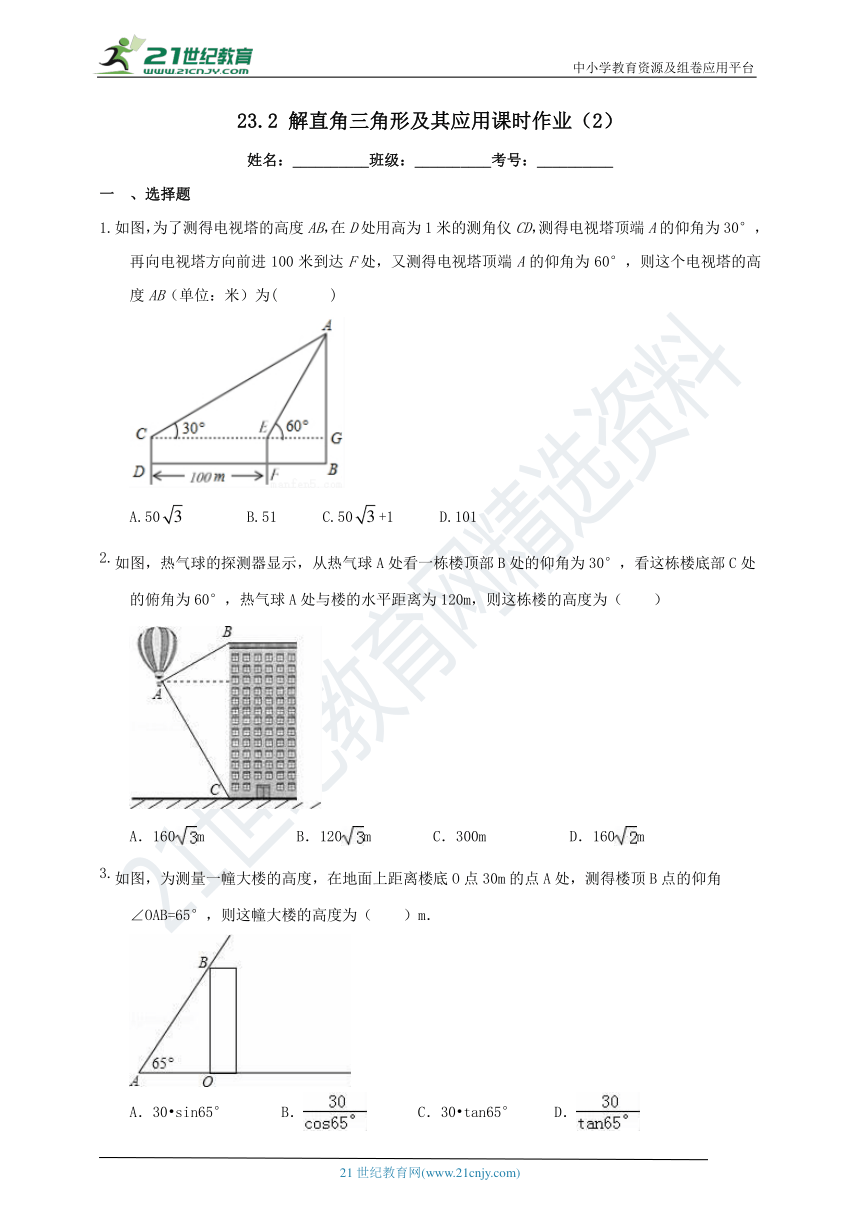
1.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B.51 C.50+1 D.101
2.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
A.160m B.120m C.300m D.160m
3.如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
A.30?sin65° B. C.30?tan65° D.
4.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是( )m.
A.20 B.30 C.30 D.40
5.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
6..如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米 B.8.9米 C.8.0米 D.5.8米
7.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是( )m.
A.20 B.30 C.30 D.40
8.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为( )
(参考数据:,,)
A. 12.6米 B. 13.1米 C. 14.7米 D. 16.3米
二 、填空题
9.观光塔是潍坊市区的标志性建筑,为测量其高度,如图 ,一人先在附近一楼房的底端A点
处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45 m,根据以上观测数据可求观光塔的高CD是__ __m.
10.如图,从楼AB的A处测得对面楼CD的顶部C的仰角为37°,底部D的俯角为45°,两楼的水平距离BD为24m,那么楼CD的高度约为 m.(结果精确到1m,参考数据:sin37°≈0.6;cos37°≈0.8;tan37°≈0.75)
11.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为_______ 米(结果保留根号).
12.如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
13.如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为 m(结果保留根号).
14.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为 m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
15.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
三 、解答题
16.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
17.如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号)
18.风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
19.热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
20.如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
21.如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
答案解析
一 、选择题
1.【分析】设AG=x,分别在Rt△AEG和Rt△ACG中,表示出CG和GE的长度,然后根据DF=100m,求出x的值,继而可求出电视塔的高度AH.
解:设AG=x,
在Rt△AEG中,
∵tan∠AEG=,
∴EG==x,
在Rt△ACG中,
∵tan∠ACG=,
∴CG==x,
∴x﹣x=100,
解得:x=50.
则AB=50+1(米).
故选C.
2.【分析】首先过点A作AD⊥BC于点D,根据题意得∠BAD=30°,∠CAD=60°,AD=120m,然后利用三角函数求解即可求得答案.
【解答】解:过点A作AD⊥BC于点D,则∠BAD=30°,∠CAD=60°,AD=120m,
在Rt△ABD中,BD=ADtan30°=120×=40(m),
在Rt△ACD中,CD=ADtan60°=120×=120(m),
∴BC=BD+CD=160(m).
故选A.
3.【考点】解直角三角形的应用-仰角俯角问题.
【分析】利用正切函数的定义tan∠BAO=即可解决.
解:如图,在RT△ABO中,∵∠AOB=90°,∠A=65°,AO=30m,
∴tan65°=,
∴BO=30?tan65°.
故选C.
【点评】本题考查解直角三角形的应用、记住三角函数的定义是解题的关键,属于基础题.
4.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE==,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===20m,
∴AB=BC?sin60°=20×=30m.
故选B.
5.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】作BM⊥ED交ED的延长线于M,CN⊥DM于N.首先解直角三角形Rt△CDN,求出CN,DN,再根据tan24°=,构建方程即可解决问题;
解:作BM⊥ED交ED的延长线于M,CN⊥DM于N.
在Rt△CDN中,∵==,设CN=4k,DN=3k,
∴CD=10,
∴(3k)2+(4k)2=100,
∴k=2,
∴CN=8,DN=6,
∵四边形BMNC是矩形,
∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66,
在Rt△AEM中,tan24°=,
∴0.45=,
∴AB=21.7(米),
故选:A.
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
6.【考点】解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.
【分析】延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴==.
设BD=5k(米),AD=12k(米),则AB=13k(米).
∵AB=13(米),
∴k=1,
∴BD=5(米),AD=12(米).
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD?tan∠CAD≈12×0.90≈10.8(米),
∴BC=10.8﹣5≈5.8(米).
故选:D.
【点评】本题考查仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
7.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE==,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===20m,
∴AB=BC?sin60°=20×=30m.
故选B.
8.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】延长AB交地面于点H,作CM⊥DE, 易得CM=1.6,DM=1.2,再由tan58°=,求得AH长即可得.
解:延长AB交地面于点H,作CM⊥DE,则四边形BHMC是矩形,
∴HM=BC=1,BH=CM,
∵,i=CM:DM,
∴DM=0.75CM,
∵DM2+CM2=CD2,,
∴CM=1.6,DM=1.2,
∴HE=HM+DM+DE=1+1.2+7=9.2,
在Rt△AHE中,∠AED=58°,∴tan58°=,
即=1.6,
∴AH=14.72,
∴AB=AH-BH=14.72-1.6=13.12≈13.1(米),
故选B.
【点睛】本题考查了解直角三角形的应用,添加辅助线构造直角三角形,从图中提取相关信息是解题的关键.
二 、填空题
9.【考点】解直角三角形的应用--仰角、俯角问题
【分析】?根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,tan30°=,
∴=,
∴AD=45,
∵在楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=AD·tan60°=45×=135(m).
【点评?】本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.
10.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】在Rt△ACE中,根据正切函数求得EC=AE?tan∠CAE,在Rt△AED中,求得ED=AE,再根据CD=DE+CE,代入数据计算即可.
解:在Rt△ACE中,
∵AE=24,∠CAE=37°,
∴CE=AE?tan37°≈24×0.75=18,
在Rt△AED中,
∵∠EAD=45°,
∴AE=ED=24,
∴DC=CE+DE=18+24≈42.
故楼BC的高度大约为42m.
11.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先求出∠ANB=45°,进而推得AN=MN,最后用等腰直角三角形的性质即可得出结论.
解:如图,
连接AN,由题意知,BM⊥AA',BA=BA'
∴AN=A'N,
∴∠ANB=∠A'NB=45°,
∵∠AMB=22.5°,
∴∠MAN=∠ANB﹣∠AMB=22.5°=∠AMN,
∴AN=MN=200米,
在Rt△ABN中,∠ANB=45°,
∴AB=AN=100(米),
故答案为100.
12.【考点】解直角三角形的应用-仰角俯角问题.
【分析】首先过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,然后在Rt△BAE中,∠BAE=60°,然后由三角形函数的知识求得BE的长,继而求得答案.
【解答】解:如图,过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,
∵在Rt△BAE中,∠BAE=60°,
∴BE=AE?tan60°=10(m),
∴BC=CE+BE=10+1(m).
∴旗杆高BC为10+1m.
故答案为:10+1.
13.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】根据三角函数和直角三角形的性质解答即可.
解:∵在点B处测得塔顶A的仰角为30°,
∴∠B=30°,
∵BC=30m,
∴AC=m,
故答案为:10
【点评】此题考查了考查仰角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.
14.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】根据三角函数和直角三角形的性质解答即可.
解:过D作DE⊥AB,
∵在D处测得旗杆顶端A的仰角为53°,
∴∠ADE=53°,
∵BC=DE=6m,
∴AE=DE?tan53°≈6×1.33≈7.98m,
∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m,
故答案为:9.5
【点评】此题考查了考查仰角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.
15.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】在Rt△ACH和Rt△HCB中,利用锐角三角函数,用CH表示出AH、BH的长,然后计算出AB的长.
解:由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB==
==1200(米).
∴AB=HB﹣HA
=1200﹣1200
=1200(﹣1)米
故答案为:1200(﹣1)
【点评】本题考查了锐角三角函数的仰角、俯角问题.题目难度不大,解决本题的关键是用含CH的式子表示出AH和BH.
三 、解答题
16.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】设楼EF的高为x米,由EG=EF﹣GF表示出EG,根据题意得到EF与AF垂直,DC与AF垂直,BA与AF垂直,BD与EF垂直,在直角三角形EGD中,利用锐角三角函数定义表示出DG,在直角三角形EGB中,利用锐角三角函数定义表示出BG,根据BG﹣DG表示出DB,即为CA,根据CA的长列出关于x的方程,求出方程的解即可得到结果.
解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米,
依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G),
在Rt△EGD中,DG==(x﹣1.5)米,在Rt△EGB中,BG=(x﹣1.5)米,
∴CA=DB=BG﹣DG=(x﹣1.5)米,
∵CA=12米,∴(x﹣1.5)=12,
解得:x=6+1.5≈11.9,
则楼EF的高度约为11.9米.
17.【考点】解直角三角形的应用-仰角俯角问题.
【分析】首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造方程关系式,进而可解即可求出答案.
【解答】解:过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.
设BC=xm.
∵∠CBE=60°,
∴BE=x,CE=x.
∵CD=200,
∴DE=200﹣x.
∴BF=DE=200﹣x,DF=BE=x.
∵∠CAD=45°,
∴AD=CD=200.
∴AF=200﹣x.
在Rt△ABF中,tan30°==,
解得x=200(﹣1)(m).
答:电缆BC至少m
【点评】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
18.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】作BE⊥DH,知GH=BE、BG=EH=10,设AH=x,则BE=GH=43+x,由CH=AHtan∠CAH=tan55°?x知CE=CH﹣EH=tan55°?x﹣10,根据BE=DE可得关于x的方程,解之可得.
解:如图,作BE⊥DH于点E,
则GH=BE、BG=EH=10,
设AH=x,则BE=GH=GA+AH=43+x,
在Rt△ACH中,CH=AHtan∠CAH=tan55°?x,
∴CE=CH﹣EH=tan55°?x﹣10,
∵∠DBE=45°,
∴BE=DE=CE+DC,即43+x=tan55°?x﹣10+35,
解得:x≈45,
∴CH=tan55°?x=1.4×45=63,
答:塔杆CH的高为63米.
19.【考点】解直角三角形的应用-仰角俯角问题
【分析】过A作AE⊥BC,交CB的延长线于点E,先解Rt△ACD,求出CD的长,则AE=CD,再解Rt△ABE,求出BE的长,然后根据BC=AD﹣BE即可得到这栋楼的高度.
解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD?tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE?tan30°=140×=140(米),[来源:学科网]
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,在此类题目中常用的方法是利用作高线转化为直角三角形进行计算.
20.【考点】解直角三角形的应用-俯角仰角
【分析】作DH⊥BC于H.设AE=x.在Rt△ABC中,根据tan∠ABC=,构建方程即可解决问题;
解:作DH⊥BC于H.设AE=x.
∵DH:BH=1:3,
在Rt△BDH中,DH2+(3DH)2=6002,
∴DH=60,BH=180,
在Rt△ADE中,∵∠ADE=45°,
∴DE=AE=x,
∵又HC=ED,EC=DH,
∴HC=x,EC=60,
在Rt△ABC中,tan33°=,
∴x=,
∴AC=AE+EC=+60=.
答:山顶A到地面BC的高度AC是米
【点评】本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.
21.【考点】解直角三角形的应用-仰角俯角问题.
【分析】过点B作BF⊥DE于点F,可得四边形ABFE为矩形,先在△BCF中求出CF的长度,然后在△BDF中求出DF的长度,最后DF﹣CF可求得CD的长度.
解:过点B作BF⊥DE于点F,
则四边形ABFE为矩形,
在△BCF中,
∵∠CBF=40°,∠CFB=90°,BF=AE=24m,
∴=tan40°,
∴CF=0.84×24≈20.16(m),
在△BDF中,
∵∠DBF=45°,
∴DF=24m,
则CD=DF﹣CF=24﹣20.16=3.84≈3.8(m).
故旗杆CD的长为3.8m.
【点评】本题考查了直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数解直角三角形.
姓名:__________班级:__________考号:__________
一 、选择题
1.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B.51 C.50+1 D.101
2.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
A.160m B.120m C.300m D.160m
3.如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
A.30?sin65° B. C.30?tan65° D.
4.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是( )m.
A.20 B.30 C.30 D.40
5.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
6..如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米 B.8.9米 C.8.0米 D.5.8米
7.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是( )m.
A.20 B.30 C.30 D.40
8.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为( )
(参考数据:,,)
A. 12.6米 B. 13.1米 C. 14.7米 D. 16.3米
二 、填空题
9.观光塔是潍坊市区的标志性建筑,为测量其高度,如图 ,一人先在附近一楼房的底端A点
处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45 m,根据以上观测数据可求观光塔的高CD是__ __m.
10.如图,从楼AB的A处测得对面楼CD的顶部C的仰角为37°,底部D的俯角为45°,两楼的水平距离BD为24m,那么楼CD的高度约为 m.(结果精确到1m,参考数据:sin37°≈0.6;cos37°≈0.8;tan37°≈0.75)
11.如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为_______ 米(结果保留根号).
12.如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
13.如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为 m(结果保留根号).
14.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为 m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
15.如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为 米(结果保留根号).
三 、解答题
16.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
17.如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号)
18.风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
19.热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
20.如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
21.如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
答案解析
一 、选择题
1.【分析】设AG=x,分别在Rt△AEG和Rt△ACG中,表示出CG和GE的长度,然后根据DF=100m,求出x的值,继而可求出电视塔的高度AH.
解:设AG=x,
在Rt△AEG中,
∵tan∠AEG=,
∴EG==x,
在Rt△ACG中,
∵tan∠ACG=,
∴CG==x,
∴x﹣x=100,
解得:x=50.
则AB=50+1(米).
故选C.
2.【分析】首先过点A作AD⊥BC于点D,根据题意得∠BAD=30°,∠CAD=60°,AD=120m,然后利用三角函数求解即可求得答案.
【解答】解:过点A作AD⊥BC于点D,则∠BAD=30°,∠CAD=60°,AD=120m,
在Rt△ABD中,BD=ADtan30°=120×=40(m),
在Rt△ACD中,CD=ADtan60°=120×=120(m),
∴BC=BD+CD=160(m).
故选A.
3.【考点】解直角三角形的应用-仰角俯角问题.
【分析】利用正切函数的定义tan∠BAO=即可解决.
解:如图,在RT△ABO中,∵∠AOB=90°,∠A=65°,AO=30m,
∴tan65°=,
∴BO=30?tan65°.
故选C.
【点评】本题考查解直角三角形的应用、记住三角函数的定义是解题的关键,属于基础题.
4.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE==,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===20m,
∴AB=BC?sin60°=20×=30m.
故选B.
5.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】作BM⊥ED交ED的延长线于M,CN⊥DM于N.首先解直角三角形Rt△CDN,求出CN,DN,再根据tan24°=,构建方程即可解决问题;
解:作BM⊥ED交ED的延长线于M,CN⊥DM于N.
在Rt△CDN中,∵==,设CN=4k,DN=3k,
∴CD=10,
∴(3k)2+(4k)2=100,
∴k=2,
∴CN=8,DN=6,
∵四边形BMNC是矩形,
∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66,
在Rt△AEM中,tan24°=,
∴0.45=,
∴AB=21.7(米),
故选:A.
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
6.【考点】解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.
【分析】延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴==.
设BD=5k(米),AD=12k(米),则AB=13k(米).
∵AB=13(米),
∴k=1,
∴BD=5(米),AD=12(米).
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD?tan∠CAD≈12×0.90≈10.8(米),
∴BC=10.8﹣5≈5.8(米).
故选:D.
【点评】本题考查仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
7.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.
解:在Rt△CDE中,
∵CD=20m,DE=10m,
∴sin∠DCE==,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===20m,
∴AB=BC?sin60°=20×=30m.
故选B.
8.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】延长AB交地面于点H,作CM⊥DE, 易得CM=1.6,DM=1.2,再由tan58°=,求得AH长即可得.
解:延长AB交地面于点H,作CM⊥DE,则四边形BHMC是矩形,
∴HM=BC=1,BH=CM,
∵,i=CM:DM,
∴DM=0.75CM,
∵DM2+CM2=CD2,,
∴CM=1.6,DM=1.2,
∴HE=HM+DM+DE=1+1.2+7=9.2,
在Rt△AHE中,∠AED=58°,∴tan58°=,
即=1.6,
∴AH=14.72,
∴AB=AH-BH=14.72-1.6=13.12≈13.1(米),
故选B.
【点睛】本题考查了解直角三角形的应用,添加辅助线构造直角三角形,从图中提取相关信息是解题的关键.
二 、填空题
9.【考点】解直角三角形的应用--仰角、俯角问题
【分析】?根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,tan30°=,
∴=,
∴AD=45,
∵在楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=AD·tan60°=45×=135(m).
【点评?】本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.
10.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】在Rt△ACE中,根据正切函数求得EC=AE?tan∠CAE,在Rt△AED中,求得ED=AE,再根据CD=DE+CE,代入数据计算即可.
解:在Rt△ACE中,
∵AE=24,∠CAE=37°,
∴CE=AE?tan37°≈24×0.75=18,
在Rt△AED中,
∵∠EAD=45°,
∴AE=ED=24,
∴DC=CE+DE=18+24≈42.
故楼BC的高度大约为42m.
11.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】先求出∠ANB=45°,进而推得AN=MN,最后用等腰直角三角形的性质即可得出结论.
解:如图,
连接AN,由题意知,BM⊥AA',BA=BA'
∴AN=A'N,
∴∠ANB=∠A'NB=45°,
∵∠AMB=22.5°,
∴∠MAN=∠ANB﹣∠AMB=22.5°=∠AMN,
∴AN=MN=200米,
在Rt△ABN中,∠ANB=45°,
∴AB=AN=100(米),
故答案为100.
12.【考点】解直角三角形的应用-仰角俯角问题.
【分析】首先过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,然后在Rt△BAE中,∠BAE=60°,然后由三角形函数的知识求得BE的长,继而求得答案.
【解答】解:如图,过点A作AE∥DC,交BC于点E,则AE=CD=10m,CE=AD=1m,
∵在Rt△BAE中,∠BAE=60°,
∴BE=AE?tan60°=10(m),
∴BC=CE+BE=10+1(m).
∴旗杆高BC为10+1m.
故答案为:10+1.
13.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】根据三角函数和直角三角形的性质解答即可.
解:∵在点B处测得塔顶A的仰角为30°,
∴∠B=30°,
∵BC=30m,
∴AC=m,
故答案为:10
【点评】此题考查了考查仰角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.
14.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】根据三角函数和直角三角形的性质解答即可.
解:过D作DE⊥AB,
∵在D处测得旗杆顶端A的仰角为53°,
∴∠ADE=53°,
∵BC=DE=6m,
∴AE=DE?tan53°≈6×1.33≈7.98m,
∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m,
故答案为:9.5
【点评】此题考查了考查仰角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.
15.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】在Rt△ACH和Rt△HCB中,利用锐角三角函数,用CH表示出AH、BH的长,然后计算出AB的长.
解:由于CD∥HB,
∴∠CAH=∠ACD=45°,∠B=∠BCD=30°
在Rt△ACH中,∵∴∠CAH=45°
∴AH=CH=1200米,
在Rt△HCB,∵tan∠B=
∴HB==
==1200(米).
∴AB=HB﹣HA
=1200﹣1200
=1200(﹣1)米
故答案为:1200(﹣1)
【点评】本题考查了锐角三角函数的仰角、俯角问题.题目难度不大,解决本题的关键是用含CH的式子表示出AH和BH.
三 、解答题
16.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】设楼EF的高为x米,由EG=EF﹣GF表示出EG,根据题意得到EF与AF垂直,DC与AF垂直,BA与AF垂直,BD与EF垂直,在直角三角形EGD中,利用锐角三角函数定义表示出DG,在直角三角形EGB中,利用锐角三角函数定义表示出BG,根据BG﹣DG表示出DB,即为CA,根据CA的长列出关于x的方程,求出方程的解即可得到结果.
解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米,
依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G),
在Rt△EGD中,DG==(x﹣1.5)米,在Rt△EGB中,BG=(x﹣1.5)米,
∴CA=DB=BG﹣DG=(x﹣1.5)米,
∵CA=12米,∴(x﹣1.5)=12,
解得:x=6+1.5≈11.9,
则楼EF的高度约为11.9米.
17.【考点】解直角三角形的应用-仰角俯角问题.
【分析】首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造方程关系式,进而可解即可求出答案.
【解答】解:过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.
设BC=xm.
∵∠CBE=60°,
∴BE=x,CE=x.
∵CD=200,
∴DE=200﹣x.
∴BF=DE=200﹣x,DF=BE=x.
∵∠CAD=45°,
∴AD=CD=200.
∴AF=200﹣x.
在Rt△ABF中,tan30°==,
解得x=200(﹣1)(m).
答:电缆BC至少m
【点评】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
18.【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】作BE⊥DH,知GH=BE、BG=EH=10,设AH=x,则BE=GH=43+x,由CH=AHtan∠CAH=tan55°?x知CE=CH﹣EH=tan55°?x﹣10,根据BE=DE可得关于x的方程,解之可得.
解:如图,作BE⊥DH于点E,
则GH=BE、BG=EH=10,
设AH=x,则BE=GH=GA+AH=43+x,
在Rt△ACH中,CH=AHtan∠CAH=tan55°?x,
∴CE=CH﹣EH=tan55°?x﹣10,
∵∠DBE=45°,
∴BE=DE=CE+DC,即43+x=tan55°?x﹣10+35,
解得:x≈45,
∴CH=tan55°?x=1.4×45=63,
答:塔杆CH的高为63米.
19.【考点】解直角三角形的应用-仰角俯角问题
【分析】过A作AE⊥BC,交CB的延长线于点E,先解Rt△ACD,求出CD的长,则AE=CD,再解Rt△ABE,求出BE的长,然后根据BC=AD﹣BE即可得到这栋楼的高度.
解:过A作AE⊥BC,交CB的延长线于点E,
在Rt△ACD中,
∵∠CAD=30°,AD=420米,
∴CD=AD?tan30°=420×=140(米),
∴AE=CD=140米.
在Rt△ABE中,
∵∠BAE=30°,AE=140米,
∴BE=AE?tan30°=140×=140(米),[来源:学科网]
∴BC=AD﹣BE=420﹣140=280(米),
答:这栋楼的高度为280米.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,在此类题目中常用的方法是利用作高线转化为直角三角形进行计算.
20.【考点】解直角三角形的应用-俯角仰角
【分析】作DH⊥BC于H.设AE=x.在Rt△ABC中,根据tan∠ABC=,构建方程即可解决问题;
解:作DH⊥BC于H.设AE=x.
∵DH:BH=1:3,
在Rt△BDH中,DH2+(3DH)2=6002,
∴DH=60,BH=180,
在Rt△ADE中,∵∠ADE=45°,
∴DE=AE=x,
∵又HC=ED,EC=DH,
∴HC=x,EC=60,
在Rt△ABC中,tan33°=,
∴x=,
∴AC=AE+EC=+60=.
答:山顶A到地面BC的高度AC是米
【点评】本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.
21.【考点】解直角三角形的应用-仰角俯角问题.
【分析】过点B作BF⊥DE于点F,可得四边形ABFE为矩形,先在△BCF中求出CF的长度,然后在△BDF中求出DF的长度,最后DF﹣CF可求得CD的长度.
解:过点B作BF⊥DE于点F,
则四边形ABFE为矩形,
在△BCF中,
∵∠CBF=40°,∠CFB=90°,BF=AE=24m,
∴=tan40°,
∴CF=0.84×24≈20.16(m),
在△BDF中,
∵∠DBF=45°,
∴DF=24m,
则CD=DF﹣CF=24﹣20.16=3.84≈3.8(m).
故旗杆CD的长为3.8m.
【点评】本题考查了直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数解直角三角形.
