第23章 解直角三角形单元检测B卷
图片预览



文档简介
第23章 解直角三角形单元检测B卷
姓名:__________班级:__________考号:__________
题号
一
二
三
总分
得分
一 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
2.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是米,测得斜坡的倾斜角是,则斜坡上相邻两树间的坡面距离约是( )(保留一位小数,)
A. 米 B. 米 C. 米 D. 米
3.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,则sinB的值是( )
A. B. C. D.
第2题 第3题 第4题
4.已知菱形ABCD,对角线AC=10 cm,BD=6 cm,,那么tan等于( )
A. B. C. D.
5.(2015秋?迁安市期末)某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为( )
A.1:2 B.1:3 C.1: D.:1
6.已知在中,,,,那么的长为( )
A. B. C. D.
7.如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20m到达处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6m,则楼房CD的高度约为( )(结果精确到0.1m,,)
A. 34.14m B. 34.1m C. 35.7m D. 35.74m
8.如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, )
A. 500 B. 518 C. 530 D. 580
9.如图,在中,,,将折叠,使点A落在BC边上的点D处,EF为折痕,若,则的值为
A. B. C. D.
10.如图,在直角△BAD中延长斜边BD到点C,使,若,则的值为( )
A. B. C. D.
11.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)
A.4.64海里 B.5.49海里 C.6.12海里 D.6.21海里
12.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A. 0组 B. 一组 C. 二组 D. 三组
二 、填空题(本大题共6小题,每小题4分,共24分)
13.在Rt△ABC中,若|sinA-1|+(-cosB)2=0,则∠C=??? .
14.如图,一人乘雪橇沿坡角为α的斜坡笔直滑行了82米,那么他下降的高度为??? 米(用含α的式子表示).
15.在地面上一点,测得电视塔尖的仰角为,沿水平方向再向塔底前行米,又测得塔尖的仰角为,那么电视塔高为??? 米.
16.中央电视台体育频道用直升机航拍技术全程直播国际马拉松比赛.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为100米,点A、D、B在同一直线上,则A、B两点的距离是??? 米.(保留根号)
17.小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E、楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A = 30(.已知楼房CD高21米,且与树BE之间的距离BC = 30米,则此树的高度约为_________米.
18.如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 .
三 、解答题(本大题共8小题,共78分)
19.计算或化简
(1)()﹣1+||+tan60°
(2)(2x+3)2﹣(2x+3)(2x﹣3)
20.如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全现要作一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的地段分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
(1)求点D与点C的高度DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)
21.如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
≈1.41,≈1.73)
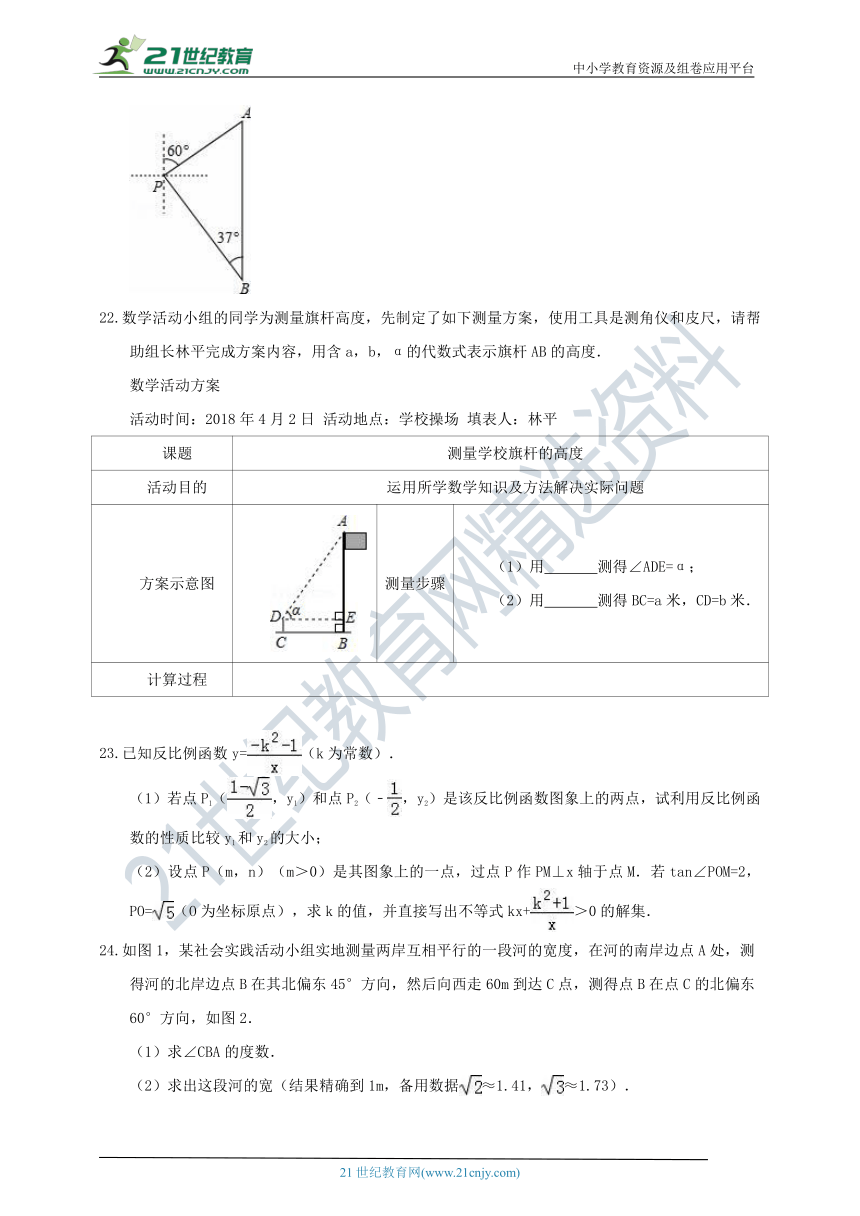
22.数学活动小组的同学为测量旗杆高度,先制定了如下测量方案,使用工具是测角仪和皮尺,请帮助组长林平完成方案内容,用含a,b,α的代数式表示旗杆AB的高度.
数学活动方案
活动时间:2018年4月2日 活动地点:学校操场 填表人:林平
课题
测量学校旗杆的高度
活动目的
运用所学数学知识及方法解决实际问题
方案示意图
测量步骤
(1)用 测得∠ADE=α;
(2)用 测得BC=a米,CD=b米.
计算过程
23.已知反比例函数y=(k为常数).
(1)若点P1(,y1)和点P2(﹣,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
(2)设点P(m,n)(m>0)是其图象上的一点,过点P作PM⊥x轴于点M.若tan∠POM=2,PO=(O为坐标原点),求k的值,并直接写出不等式kx+>0的解集.
24.如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据≈1.41,≈1.73).
25.阅读下面的材料,先完成阅读填空,再按要求答题: sin30°=,cos30°=,则sin230°+cos230°= ;① sin45°=,cos45°=,则sin245°+cos245°= ;② sin60°=,cos60°=,则sin260°+cos260°= ;③ … 观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A= ;④ (1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对∠A证明你的猜想; (2)已知:∠A为锐角(cosA>0)且sinA=,求cosA.
26.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
答案解析
一、选择题
1.【考点】解直角三角形.
【分析】根据cosB=及特殊角的三角函数值解题即可.
解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,
cosB=,
即cos30°=,
∴BC=8×=4;
故选:D.
【点评】本题考查了三角函数的定义及特殊角的三角函数值,是基础知识,需要熟练掌握.
2.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】由题意可知∠ABC=90°,利用30°角的余弦即可求出AB的长.
解:∵
∴
∵AC=3米,
∴米,
∵
∴AB=1.5×1.732≈2.6米.
故选:A.
【点睛】考查解直角三角形的应用-坡角问题,熟练掌握余弦的定义是解题的关键.
3.【考点】锐角三角函数的定义.
【分析】首先根据勾股定理求得AC的长,然后利用正弦函数的定义即可求解.
解:∵在Rt△ABC中,∠C=90°,AB=5,BC=4,
∴AC===3,
∴sinB==.
故选D.
【点评】本题考查了三角函数的定义,求锐角的三角函数值的方法:利用锐角三角函数的定义,转化成直角三角形的边长的比.
4.【考点】菱形的性质,锐三角函数的定义
【分析】利用菱形的性质锐三角函数的定义求解
解:菱形的对角线互相垂直且平分,由三角函数定义,得tan=tan∠DAC=.
故选A
5.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】根据坡面距离和垂直距离,利用勾股定理求出水平距离,然后求出坡度.
解:水平距离==4,
则坡度为:2:4=1:2.
故选A.
6.【考点】锐角三角函数
【分析】利用∠A的余弦值解答即可.
解:∵cosA=,∠A=α,AC=3,
∴AB=,
故选D.
【点睛】考查解直角三角形的知识;掌握和一个角的邻边与斜边有关的三角函数值是余弦值的知识是解决本题的关键.
7.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】过点B作BF⊥CD于F,于是得到A′B′=CF=AB=1.6米,解直角三角即可得.
解:过点B作BF⊥CD于F,
∴A′B′=CF=AB=1.6米,
在Rt△DFB′中,B′F=,
在Rt△DFB中,BF= DF,
∵BB′=AA′=20,
∴BF-B′F=DF-=20,
∴DF≈3.41,
∴CD=DF+CF=35.7米,
故选C.
【点睛】本题考查了解直角三角形的应用——仰角俯角问题,根据题意添加辅助线构造直角三角形,并结合图形利用三角函数解直角三角形进行求解是关键.
8.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
解:作BH⊥AF于H,如图,
∵斜坡AB的坡度i=1:2,
∴设BH=k,AH=2k,
∴AB=k=800,
∴k=,
∴BH=≈356,
∴EF=BH=356m;
在Rt△CBE中,∵sin∠CBE=,
∴CE=200?sin50°=200×0.8=160,
∴CF=CE+EF=160+356=516(m).
答:山CF的高度约为516米.
故选B.
【点睛】本题考查了解直角三角形的应用-坡度与坡角问题:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i═tanα.
9.【考点】三角函数锐角-正弦,翻折变换的性质、全等三角形的判定与性质、三角形内角和定理
【分析】由题意得:△AEF≌△DEF,故∠EDF=∠A;由三角形的内角和定理及平角的知识问题即可解决.
解:在中,,,
,
由折叠的性质得到:≌,
,
,
,
,
又,
,
在直角中,,
,
故选A.
【点睛】本题考查了翻折变换的性质、全等三角形的判定与性质、三角形内角和定理,三角函数等,熟练掌握相关的性质及定理是解题的关键.
10.【考点】锐角三角函数定义,相似三角形的判定和性质
【分析】延长AD,过点C作CE⊥AD的延长线,垂足为点E,由tanB=,得到AD:AB=5:3,可设AD=5x,则AB=3x;
证明△CDE∽△BDA,然后根据相似三角形的对应边成比例可用x表示出DE、CE、AE的长,最后根据正切的定义解答
解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,
即AD:AB=5:3,
∴设AD=5x,则AB=3x.
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴CE:AB=DE:AD=CD:BD=1:2,
∴CE=x,DE=x,
∴AE=x,
∴tan∠CAD= =.
故选D.
【点睛】本题考查了锐角三角函数的定义,相似三角形的判定和性质以及直角三角形的性质,是基础知识,要熟练掌握,解题的关键是正确添加辅助线,将∠CAD放在直角三角形中进行分析求解.
11.【考点】勾股定理的应用;解直角三角形的应用﹣方向角问题
【分析】根据题意画出图形,结合图形知∠BAC=30°、∠ACB=15°,作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,设BD=x,则AB=BE=CE=2x、AD=DE=x,据此得出AC=2x+2x,根据题意列出方程,求解可得.
解:如图所示,
由题意知,∠BAC=30°、∠ACB=15°,
作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,
则∠BED=30°,BE=CE,
设BD=x,
则AB=BE=CE=2x,AD=DE=x,
∴AC=AD+DE+CE=2x+2x,
∵AC=30,
∴2x+2x=30,
解得:x=≈5.49,
故选:B.
【点评】此题考查了解直角三角形的应用﹣方向角问题,涉及的知识有:三角形的外角性质,等腰三角形的判定,含30°角直角三角形的性质,以及垂线段最短的应用,其中理解题意,画出相应的图形,把实际问题转化为数学问题是解此类题的关键.
12.【考点】解直角三角形的应用
【分析】根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于(1)(3),根据AB=即可解答.
解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故选D.
【点评】本题考查解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形,解直角三角形即可求出.
二、填空题
13.【分析】根据题意可得sinA=1,cosB=,根据特殊角的三角函数值可得∠A,∠B的度数,继而求得∠C的度数. 解:由题意得:sinA=1,cosB=, 可得∠A=90°,∠B=30°, 故∠C=180°-∠A-∠B=60°. 故答案为:60°.
14.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】如图,设下滑的距离为AB=82米,下降的高度为线段AC.解直角三角形求出AC即可;
解:如图,设下滑的距离为AB=82米,下降的高度为线段AC.
在Rt△ABC中,AC=AB?sinα=82?sinα,
故答案为82?sinα.
【点睛】本题考查解直角三角形的应用,解题的关键是理解题意,属于中考常考题型.
15.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】如图:构建直角三角形,根据45°、60°角的正切值分别表示出两个三角形中CD和BD的长,然后根据二者之间的关系,列方程解答.
解:如图:设CD为x米,
∵∠CAD=45°,
∴CD=AD=x,
∵∠CBD=60°,
∴tan60°== = ,
解得:x= ,
故答案为:
故答案为:
【点睛】本题考查仰角的定义,借助仰角构造直角三角形并解直角三角形是解题关键.
16.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】由题意可知,在△ACD和△BCD中,∠CDA=∠CDB=90°,∠A=30°,∠B=45°,CD=100米,由此在△ACD和△BCD中分别求出AD和BD的长即可由AB=AD+BD求得A、B间的距离了.
解:由已知可得∠A=30°,∠B=45°,CD=100m,
∵CD⊥AB于点D.
∴在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==(m),
在Rt△BCD中,∠CDB=90°,∠B=45°
∴DB=CD=100m,
∴AB=AD+DB=100(+1)m,
故答案为:(100+100).
【点睛】读懂题意,得到“△ACD和△BCD中,∠CDA=∠CDB=90°,∠A=30°,∠B=45°,CD=100米”,这样就可以利用“解直角三角形”的方法求得AD和BD的长,从而求出A、B间的距离了.
17.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】利用CD及相应的三角函数表示出AC长,减去BC即为AB,进而利用30°的正切函数求BE长.
解:根据题意可得:
AC==21,
则AB=AC-BC=21-30.
故树高BE=AB×tan30°=(21-30)×tan30°≈(21-10)(米).
故答案为:(21-10)米.
【点睛】本题主要考查利用解直角三角形知识解决实际问题的能力.
18.【考点】 旋转的性质; 等边三角形的性质; 解直角三角形.
【分析】连接PP′,如图,先利用旋转的性质得CP=CP′=6,∠PCP′=60°,则可判定△CPP′为等边三角形得到PP′=PC=6,再证明△PCB≌△P′CA得到PB=P′A=10,接着利用勾股定理的逆定理证明△APP′为直角三角形,∠APP′=90°,然后根据正弦的定义求解.
解:连接PP′,如图,
∵线段PC绕点C顺时针旋转60°得到P'C,
∴CP=CP′=6,∠PCP′=60°,
∴△CPP′为等边三角形,
∴PP′=PC=6,
∵△ABC为等边三角形,
∴CB=CA,∠ACB=60°,
∴∠PCB=∠P′CA,
在△PCB和△P′CA中
,
∴△PCB≌△P′CA,
∴PB=P′A=10,
∵62+82=102,
∴PP′2+AP2=P′A2,
∴△APP′为直角三角形,∠APP′=90°,
∴sin∠PAP′===.
故答案为.
三、解答题
19.【考点】实数的运算;完全平方公式;平方差公式;负整数指数幂;特殊角的三角函数值
【分析】(1)根据负整数幂、绝对值的运算法则和特殊三角函数值即可化简求值.
(2)利用完全平方公式和平方差公式即可.
解:(1)()﹣1+||+tan60°
=2+(2﹣)+
=2+2﹣+
=4
(2)(2x+3)2﹣(2x+3)(2x﹣3)
=(2x)2+12x+9﹣[(2x)2﹣9]
=(2x)2+12x+9﹣(2x)2+9
=12x+18
【点评】本题考查实数的混合运算和乘法公式,负整数指数幂的运算和相反数容易混淆,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
20.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】(1)根据图形求出即可;
(2)过B作BM⊥AD于M,先求出AM,再解直角三角形求出即可.
解:(1)DH=1.5米×=1.2米;
(2)过B作BM⊥AD于M,在矩形BCHM中,MH=BC=1米,AM=AD+DH﹣MH=1米+1.2米﹣1米=1.2米=1.2米,在Rt△AMB中,AB=≈3.0米,所以有不锈钢材料的总长度为1米+3.0米+1米=5.0米.
21.【考点】解直角三角形的应用-方向角问题.
【分析】过点P作PH⊥AB于H,在Rt△APH中,根据已知条件和正弦定理求出PH,在Rt△PBH中,根据PH=100,∠B=37°,得出sin37°=,求出PB即可.
解:过点P作PH⊥AB于H,
在Rt△APH中,
∵AP=200,∠PAH=60°,
∴PH=sin60°?AP=100,
在Rt△PBH中,PH=100,∠B=37°,
∴sin37°=,
∴PB=≈≈288(米),
答:P、B两点相距约288米.
【点评】此题考查了解直角三角形,是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
22.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】在Rt△ADE中,求出AE,再利用AB=AE+BE计算即可;
解:(1)用 测角仪测得∠ADE=α;
(2)用 皮尺测得BC=a米,CD=b米.
(3)计算过程:∵四边形BCDE是矩形,
∴DE=BC=a,BE=CD=b,
在Rt△ADE中,AE=ED?tanα=a?tanα,
∴AB=AE+EB=a?tanα+b.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
23.【考点】反比例函数图象上点的坐标特征;解直角三角形.
【分析】(1)先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据P1、P2两点的横坐标判断出两点所在的象限,故可得出结论.
(2)根据题意求得﹣n=2m,根据勾股定理求得m=1,n=﹣2,得到P(1,﹣2),即可得到﹣k2﹣1=﹣2,即可求得k的值,然后分两种情况借助反比例函数和正比例函数图象即可求得.
解:(1)∵﹣k2﹣1<0,
∴反比例函数y=在每一个象限內y随x的增大而增大,
∵﹣<<0,
∴y1>y2;
(2)点P(m,n)在反比例函数y=的图象上,m>0,
∴n<0,
∴OM=m,PM=﹣n,
∵tan∠POM=2,
∴==2,
∴﹣n=2m,
∵PO=,
∴m2+(﹣n)2=5,
∴m=1,n=﹣2,
∴P(1,﹣2),
∴﹣k2﹣1=﹣2,
解得k=±1,
①当k=﹣1时,则不等式kx+>0的解集为:x<﹣或0<x<;
②当k=1时,则不等式kx+>0的解集为:x>0.
24.【考点】解直角三角形的应用-方向角问题.
【分析】(1)根据三角形的外角的性质、结合题意计算即可;
(2)作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
解:(1)由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°;
(2)作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=≈82,
答:这段河的宽约为82m.
25.【考点】同角三角函数的关系,勾股定理,锐角三角函数的定义
【分析】①②③将特殊角的三角函数值代入计算即可求出其值; ④由前面①②③的结论,即可猜想出:对任意锐角A,都有sin2A+cos2A=1; (1)如图,过点B作BD⊥AC于D,则∠ADB=90°.
利用锐角三角函数的定义得出sinA=,cosA=,则sin2A+cos2A=,再根据勾股定理得到BD2+AD2=AB2,从而证明sin2A+cos2A=1; (2)利用关系式sin2A+cos2A=1,结合已知条件cosA>0且sinA=,进行求解.
解:∵sin30°=,cos30°=, ∴sin230°+cos230°=()2+()2=+=1;① ∵sin45°=,cos45°=, ∴sin245°+cos245°=()2+()2=+=1;② ∵sin60°=,cos60°=, ∴sin260°+cos260°=()2+()2=+=1.③ 观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=1.④ (1)如图,过点B作BD⊥AC于D,则∠ADB=90°. ∵sinA=,cosA=, ∴sin2A+cos2A=()2+()2=, ∵∠ADB=90°, ∴BD2+AD2=AB2, ∴sin2A+cos2A=1.
(2)∵sinA=,sin2A+cos2A=1,∠A为锐角, ∴cosA=.
【点评】本题考查了同角三角函数的关系,勾股定理,锐角三角函数的定义,比较简单.
26.【考点】三角函数锐角-正弦,勾股定理及其逆定理
【分析】 (1)直接利用网格结合平行线的判定方法得出D点位置;
(2)直接利用勾股定理得出DC的长;
(3)利用勾股定理的逆定理得出△ACD是直角三角形,进而得出答案;
(4)根据直角三角形斜边上的中线等于斜边的一半得出AE=EC,可得∠ACB=∠CAE,然后在Rt△ABC中求出tan∠ACB的值即为tan∠CAE的值.
试题解析:
解:(1)如图所示:
D点即为所求;
(2)DC==;
故答案为:;
(3)在△ACD的三个内角中所选的锐角是:∠CAD,
∵CD=,AD=5,AC=,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴∠CAD它所对应的正弦函数值是:=;
当所选的锐角是:∠ADC,
则∠ADC它所对应的正弦函数值是:=.
故答案为:∠CAD,或∠ADC,;
(4)AB=,AC=,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=EC,
∴∠ACB=∠CAE,
∴tan∠CAE=tan∠ACB===.
故答案为:.
【点睛】本题考查了勾股定理及其逆定理和锐角三角形函数,根据勾股定理得出线段的长,根据勾股定理的逆定理得出直角三角形是解决此题的关键.
姓名:__________班级:__________考号:__________
题号
一
二
三
总分
得分
一 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
A. B.4 C.8 D.4
2.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是米,测得斜坡的倾斜角是,则斜坡上相邻两树间的坡面距离约是( )(保留一位小数,)
A. 米 B. 米 C. 米 D. 米
3.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,则sinB的值是( )
A. B. C. D.
第2题 第3题 第4题
4.已知菱形ABCD,对角线AC=10 cm,BD=6 cm,,那么tan等于( )
A. B. C. D.
5.(2015秋?迁安市期末)某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为2米,则这个坡面的坡度为( )
A.1:2 B.1:3 C.1: D.:1
6.已知在中,,,,那么的长为( )
A. B. C. D.
7.如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20m到达处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6m,则楼房CD的高度约为( )(结果精确到0.1m,,)
A. 34.14m B. 34.1m C. 35.7m D. 35.74m
8.如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, )
A. 500 B. 518 C. 530 D. 580
9.如图,在中,,,将折叠,使点A落在BC边上的点D处,EF为折痕,若,则的值为
A. B. C. D.
10.如图,在直角△BAD中延长斜边BD到点C,使,若,则的值为( )
A. B. C. D.
11.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)
A.4.64海里 B.5.49海里 C.6.12海里 D.6.21海里
12.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A. 0组 B. 一组 C. 二组 D. 三组
二 、填空题(本大题共6小题,每小题4分,共24分)
13.在Rt△ABC中,若|sinA-1|+(-cosB)2=0,则∠C=??? .
14.如图,一人乘雪橇沿坡角为α的斜坡笔直滑行了82米,那么他下降的高度为??? 米(用含α的式子表示).
15.在地面上一点,测得电视塔尖的仰角为,沿水平方向再向塔底前行米,又测得塔尖的仰角为,那么电视塔高为??? 米.
16.中央电视台体育频道用直升机航拍技术全程直播国际马拉松比赛.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为100米,点A、D、B在同一直线上,则A、B两点的距离是??? 米.(保留根号)
17.小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E、楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A = 30(.已知楼房CD高21米,且与树BE之间的距离BC = 30米,则此树的高度约为_________米.
18.如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 .
三 、解答题(本大题共8小题,共78分)
19.计算或化简
(1)()﹣1+||+tan60°
(2)(2x+3)2﹣(2x+3)(2x﹣3)
20.如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全现要作一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的地段分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
(1)求点D与点C的高度DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)
21.如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
≈1.41,≈1.73)
22.数学活动小组的同学为测量旗杆高度,先制定了如下测量方案,使用工具是测角仪和皮尺,请帮助组长林平完成方案内容,用含a,b,α的代数式表示旗杆AB的高度.
数学活动方案
活动时间:2018年4月2日 活动地点:学校操场 填表人:林平
课题
测量学校旗杆的高度
活动目的
运用所学数学知识及方法解决实际问题
方案示意图
测量步骤
(1)用 测得∠ADE=α;
(2)用 测得BC=a米,CD=b米.
计算过程
23.已知反比例函数y=(k为常数).
(1)若点P1(,y1)和点P2(﹣,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
(2)设点P(m,n)(m>0)是其图象上的一点,过点P作PM⊥x轴于点M.若tan∠POM=2,PO=(O为坐标原点),求k的值,并直接写出不等式kx+>0的解集.
24.如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据≈1.41,≈1.73).
25.阅读下面的材料,先完成阅读填空,再按要求答题: sin30°=,cos30°=,则sin230°+cos230°= ;① sin45°=,cos45°=,则sin245°+cos245°= ;② sin60°=,cos60°=,则sin260°+cos260°= ;③ … 观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A= ;④ (1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对∠A证明你的猜想; (2)已知:∠A为锐角(cosA>0)且sinA=,求cosA.
26.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
答案解析
一、选择题
1.【考点】解直角三角形.
【分析】根据cosB=及特殊角的三角函数值解题即可.
解:∵在Rt△ABC中,∠C=90°,∠B=30°,AB=8,
cosB=,
即cos30°=,
∴BC=8×=4;
故选:D.
【点评】本题考查了三角函数的定义及特殊角的三角函数值,是基础知识,需要熟练掌握.
2.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】由题意可知∠ABC=90°,利用30°角的余弦即可求出AB的长.
解:∵
∴
∵AC=3米,
∴米,
∵
∴AB=1.5×1.732≈2.6米.
故选:A.
【点睛】考查解直角三角形的应用-坡角问题,熟练掌握余弦的定义是解题的关键.
3.【考点】锐角三角函数的定义.
【分析】首先根据勾股定理求得AC的长,然后利用正弦函数的定义即可求解.
解:∵在Rt△ABC中,∠C=90°,AB=5,BC=4,
∴AC===3,
∴sinB==.
故选D.
【点评】本题考查了三角函数的定义,求锐角的三角函数值的方法:利用锐角三角函数的定义,转化成直角三角形的边长的比.
4.【考点】菱形的性质,锐三角函数的定义
【分析】利用菱形的性质锐三角函数的定义求解
解:菱形的对角线互相垂直且平分,由三角函数定义,得tan=tan∠DAC=.
故选A
5.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】根据坡面距离和垂直距离,利用勾股定理求出水平距离,然后求出坡度.
解:水平距离==4,
则坡度为:2:4=1:2.
故选A.
6.【考点】锐角三角函数
【分析】利用∠A的余弦值解答即可.
解:∵cosA=,∠A=α,AC=3,
∴AB=,
故选D.
【点睛】考查解直角三角形的知识;掌握和一个角的邻边与斜边有关的三角函数值是余弦值的知识是解决本题的关键.
7.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】过点B作BF⊥CD于F,于是得到A′B′=CF=AB=1.6米,解直角三角即可得.
解:过点B作BF⊥CD于F,
∴A′B′=CF=AB=1.6米,
在Rt△DFB′中,B′F=,
在Rt△DFB中,BF= DF,
∵BB′=AA′=20,
∴BF-B′F=DF-=20,
∴DF≈3.41,
∴CD=DF+CF=35.7米,
故选C.
【点睛】本题考查了解直角三角形的应用——仰角俯角问题,根据题意添加辅助线构造直角三角形,并结合图形利用三角函数解直角三角形进行求解是关键.
8.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
解:作BH⊥AF于H,如图,
∵斜坡AB的坡度i=1:2,
∴设BH=k,AH=2k,
∴AB=k=800,
∴k=,
∴BH=≈356,
∴EF=BH=356m;
在Rt△CBE中,∵sin∠CBE=,
∴CE=200?sin50°=200×0.8=160,
∴CF=CE+EF=160+356=516(m).
答:山CF的高度约为516米.
故选B.
【点睛】本题考查了解直角三角形的应用-坡度与坡角问题:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i═tanα.
9.【考点】三角函数锐角-正弦,翻折变换的性质、全等三角形的判定与性质、三角形内角和定理
【分析】由题意得:△AEF≌△DEF,故∠EDF=∠A;由三角形的内角和定理及平角的知识问题即可解决.
解:在中,,,
,
由折叠的性质得到:≌,
,
,
,
,
又,
,
在直角中,,
,
故选A.
【点睛】本题考查了翻折变换的性质、全等三角形的判定与性质、三角形内角和定理,三角函数等,熟练掌握相关的性质及定理是解题的关键.
10.【考点】锐角三角函数定义,相似三角形的判定和性质
【分析】延长AD,过点C作CE⊥AD的延长线,垂足为点E,由tanB=,得到AD:AB=5:3,可设AD=5x,则AB=3x;
证明△CDE∽△BDA,然后根据相似三角形的对应边成比例可用x表示出DE、CE、AE的长,最后根据正切的定义解答
解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,
即AD:AB=5:3,
∴设AD=5x,则AB=3x.
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴CE:AB=DE:AD=CD:BD=1:2,
∴CE=x,DE=x,
∴AE=x,
∴tan∠CAD= =.
故选D.
【点睛】本题考查了锐角三角函数的定义,相似三角形的判定和性质以及直角三角形的性质,是基础知识,要熟练掌握,解题的关键是正确添加辅助线,将∠CAD放在直角三角形中进行分析求解.
11.【考点】勾股定理的应用;解直角三角形的应用﹣方向角问题
【分析】根据题意画出图形,结合图形知∠BAC=30°、∠ACB=15°,作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,设BD=x,则AB=BE=CE=2x、AD=DE=x,据此得出AC=2x+2x,根据题意列出方程,求解可得.
解:如图所示,
由题意知,∠BAC=30°、∠ACB=15°,
作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,
则∠BED=30°,BE=CE,
设BD=x,
则AB=BE=CE=2x,AD=DE=x,
∴AC=AD+DE+CE=2x+2x,
∵AC=30,
∴2x+2x=30,
解得:x=≈5.49,
故选:B.
【点评】此题考查了解直角三角形的应用﹣方向角问题,涉及的知识有:三角形的外角性质,等腰三角形的判定,含30°角直角三角形的性质,以及垂线段最短的应用,其中理解题意,画出相应的图形,把实际问题转化为数学问题是解此类题的关键.
12.【考点】解直角三角形的应用
【分析】根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于(1)(3),根据AB=即可解答.
解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故选D.
【点评】本题考查解直角三角形的应用,解答道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形,解直角三角形即可求出.
二、填空题
13.【分析】根据题意可得sinA=1,cosB=,根据特殊角的三角函数值可得∠A,∠B的度数,继而求得∠C的度数. 解:由题意得:sinA=1,cosB=, 可得∠A=90°,∠B=30°, 故∠C=180°-∠A-∠B=60°. 故答案为:60°.
14.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】如图,设下滑的距离为AB=82米,下降的高度为线段AC.解直角三角形求出AC即可;
解:如图,设下滑的距离为AB=82米,下降的高度为线段AC.
在Rt△ABC中,AC=AB?sinα=82?sinα,
故答案为82?sinα.
【点睛】本题考查解直角三角形的应用,解题的关键是理解题意,属于中考常考题型.
15.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】如图:构建直角三角形,根据45°、60°角的正切值分别表示出两个三角形中CD和BD的长,然后根据二者之间的关系,列方程解答.
解:如图:设CD为x米,
∵∠CAD=45°,
∴CD=AD=x,
∵∠CBD=60°,
∴tan60°== = ,
解得:x= ,
故答案为:
故答案为:
【点睛】本题考查仰角的定义,借助仰角构造直角三角形并解直角三角形是解题关键.
16.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】由题意可知,在△ACD和△BCD中,∠CDA=∠CDB=90°,∠A=30°,∠B=45°,CD=100米,由此在△ACD和△BCD中分别求出AD和BD的长即可由AB=AD+BD求得A、B间的距离了.
解:由已知可得∠A=30°,∠B=45°,CD=100m,
∵CD⊥AB于点D.
∴在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==(m),
在Rt△BCD中,∠CDB=90°,∠B=45°
∴DB=CD=100m,
∴AB=AD+DB=100(+1)m,
故答案为:(100+100).
【点睛】读懂题意,得到“△ACD和△BCD中,∠CDA=∠CDB=90°,∠A=30°,∠B=45°,CD=100米”,这样就可以利用“解直角三角形”的方法求得AD和BD的长,从而求出A、B间的距离了.
17.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】利用CD及相应的三角函数表示出AC长,减去BC即为AB,进而利用30°的正切函数求BE长.
解:根据题意可得:
AC==21,
则AB=AC-BC=21-30.
故树高BE=AB×tan30°=(21-30)×tan30°≈(21-10)(米).
故答案为:(21-10)米.
【点睛】本题主要考查利用解直角三角形知识解决实际问题的能力.
18.【考点】 旋转的性质; 等边三角形的性质; 解直角三角形.
【分析】连接PP′,如图,先利用旋转的性质得CP=CP′=6,∠PCP′=60°,则可判定△CPP′为等边三角形得到PP′=PC=6,再证明△PCB≌△P′CA得到PB=P′A=10,接着利用勾股定理的逆定理证明△APP′为直角三角形,∠APP′=90°,然后根据正弦的定义求解.
解:连接PP′,如图,
∵线段PC绕点C顺时针旋转60°得到P'C,
∴CP=CP′=6,∠PCP′=60°,
∴△CPP′为等边三角形,
∴PP′=PC=6,
∵△ABC为等边三角形,
∴CB=CA,∠ACB=60°,
∴∠PCB=∠P′CA,
在△PCB和△P′CA中
,
∴△PCB≌△P′CA,
∴PB=P′A=10,
∵62+82=102,
∴PP′2+AP2=P′A2,
∴△APP′为直角三角形,∠APP′=90°,
∴sin∠PAP′===.
故答案为.
三、解答题
19.【考点】实数的运算;完全平方公式;平方差公式;负整数指数幂;特殊角的三角函数值
【分析】(1)根据负整数幂、绝对值的运算法则和特殊三角函数值即可化简求值.
(2)利用完全平方公式和平方差公式即可.
解:(1)()﹣1+||+tan60°
=2+(2﹣)+
=2+2﹣+
=4
(2)(2x+3)2﹣(2x+3)(2x﹣3)
=(2x)2+12x+9﹣[(2x)2﹣9]
=(2x)2+12x+9﹣(2x)2+9
=12x+18
【点评】本题考查实数的混合运算和乘法公式,负整数指数幂的运算和相反数容易混淆,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
20.【考点】解直角三角形的应用﹣坡度坡角问题
【分析】(1)根据图形求出即可;
(2)过B作BM⊥AD于M,先求出AM,再解直角三角形求出即可.
解:(1)DH=1.5米×=1.2米;
(2)过B作BM⊥AD于M,在矩形BCHM中,MH=BC=1米,AM=AD+DH﹣MH=1米+1.2米﹣1米=1.2米=1.2米,在Rt△AMB中,AB=≈3.0米,所以有不锈钢材料的总长度为1米+3.0米+1米=5.0米.
21.【考点】解直角三角形的应用-方向角问题.
【分析】过点P作PH⊥AB于H,在Rt△APH中,根据已知条件和正弦定理求出PH,在Rt△PBH中,根据PH=100,∠B=37°,得出sin37°=,求出PB即可.
解:过点P作PH⊥AB于H,
在Rt△APH中,
∵AP=200,∠PAH=60°,
∴PH=sin60°?AP=100,
在Rt△PBH中,PH=100,∠B=37°,
∴sin37°=,
∴PB=≈≈288(米),
答:P、B两点相距约288米.
【点评】此题考查了解直角三角形,是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
22.【考点】解直角三角形的应用﹣仰角俯角问题
【分析】在Rt△ADE中,求出AE,再利用AB=AE+BE计算即可;
解:(1)用 测角仪测得∠ADE=α;
(2)用 皮尺测得BC=a米,CD=b米.
(3)计算过程:∵四边形BCDE是矩形,
∴DE=BC=a,BE=CD=b,
在Rt△ADE中,AE=ED?tanα=a?tanα,
∴AB=AE+EB=a?tanα+b.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
23.【考点】反比例函数图象上点的坐标特征;解直角三角形.
【分析】(1)先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据P1、P2两点的横坐标判断出两点所在的象限,故可得出结论.
(2)根据题意求得﹣n=2m,根据勾股定理求得m=1,n=﹣2,得到P(1,﹣2),即可得到﹣k2﹣1=﹣2,即可求得k的值,然后分两种情况借助反比例函数和正比例函数图象即可求得.
解:(1)∵﹣k2﹣1<0,
∴反比例函数y=在每一个象限內y随x的增大而增大,
∵﹣<<0,
∴y1>y2;
(2)点P(m,n)在反比例函数y=的图象上,m>0,
∴n<0,
∴OM=m,PM=﹣n,
∵tan∠POM=2,
∴==2,
∴﹣n=2m,
∵PO=,
∴m2+(﹣n)2=5,
∴m=1,n=﹣2,
∴P(1,﹣2),
∴﹣k2﹣1=﹣2,
解得k=±1,
①当k=﹣1时,则不等式kx+>0的解集为:x<﹣或0<x<;
②当k=1时,则不等式kx+>0的解集为:x>0.
24.【考点】解直角三角形的应用-方向角问题.
【分析】(1)根据三角形的外角的性质、结合题意计算即可;
(2)作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
解:(1)由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°;
(2)作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=≈82,
答:这段河的宽约为82m.
25.【考点】同角三角函数的关系,勾股定理,锐角三角函数的定义
【分析】①②③将特殊角的三角函数值代入计算即可求出其值; ④由前面①②③的结论,即可猜想出:对任意锐角A,都有sin2A+cos2A=1; (1)如图,过点B作BD⊥AC于D,则∠ADB=90°.
利用锐角三角函数的定义得出sinA=,cosA=,则sin2A+cos2A=,再根据勾股定理得到BD2+AD2=AB2,从而证明sin2A+cos2A=1; (2)利用关系式sin2A+cos2A=1,结合已知条件cosA>0且sinA=,进行求解.
解:∵sin30°=,cos30°=, ∴sin230°+cos230°=()2+()2=+=1;① ∵sin45°=,cos45°=, ∴sin245°+cos245°=()2+()2=+=1;② ∵sin60°=,cos60°=, ∴sin260°+cos260°=()2+()2=+=1.③ 观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=1.④ (1)如图,过点B作BD⊥AC于D,则∠ADB=90°. ∵sinA=,cosA=, ∴sin2A+cos2A=()2+()2=, ∵∠ADB=90°, ∴BD2+AD2=AB2, ∴sin2A+cos2A=1.
(2)∵sinA=,sin2A+cos2A=1,∠A为锐角, ∴cosA=.
【点评】本题考查了同角三角函数的关系,勾股定理,锐角三角函数的定义,比较简单.
26.【考点】三角函数锐角-正弦,勾股定理及其逆定理
【分析】 (1)直接利用网格结合平行线的判定方法得出D点位置;
(2)直接利用勾股定理得出DC的长;
(3)利用勾股定理的逆定理得出△ACD是直角三角形,进而得出答案;
(4)根据直角三角形斜边上的中线等于斜边的一半得出AE=EC,可得∠ACB=∠CAE,然后在Rt△ABC中求出tan∠ACB的值即为tan∠CAE的值.
试题解析:
解:(1)如图所示:
D点即为所求;
(2)DC==;
故答案为:;
(3)在△ACD的三个内角中所选的锐角是:∠CAD,
∵CD=,AD=5,AC=,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴∠CAD它所对应的正弦函数值是:=;
当所选的锐角是:∠ADC,
则∠ADC它所对应的正弦函数值是:=.
故答案为:∠CAD,或∠ADC,;
(4)AB=,AC=,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=EC,
∴∠ACB=∠CAE,
∴tan∠CAE=tan∠ACB===.
故答案为:.
【点睛】本题考查了勾股定理及其逆定理和锐角三角形函数,根据勾股定理得出线段的长,根据勾股定理的逆定理得出直角三角形是解决此题的关键.
