第23章 解直角三角形单元检测A卷

中小学教育资源及组卷应用平台


第23章 解直角三角形单元检测A卷
姓名：__________班级：__________考号：__________
一 、选择题（本大题共12小题，每小题4分，共48分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）
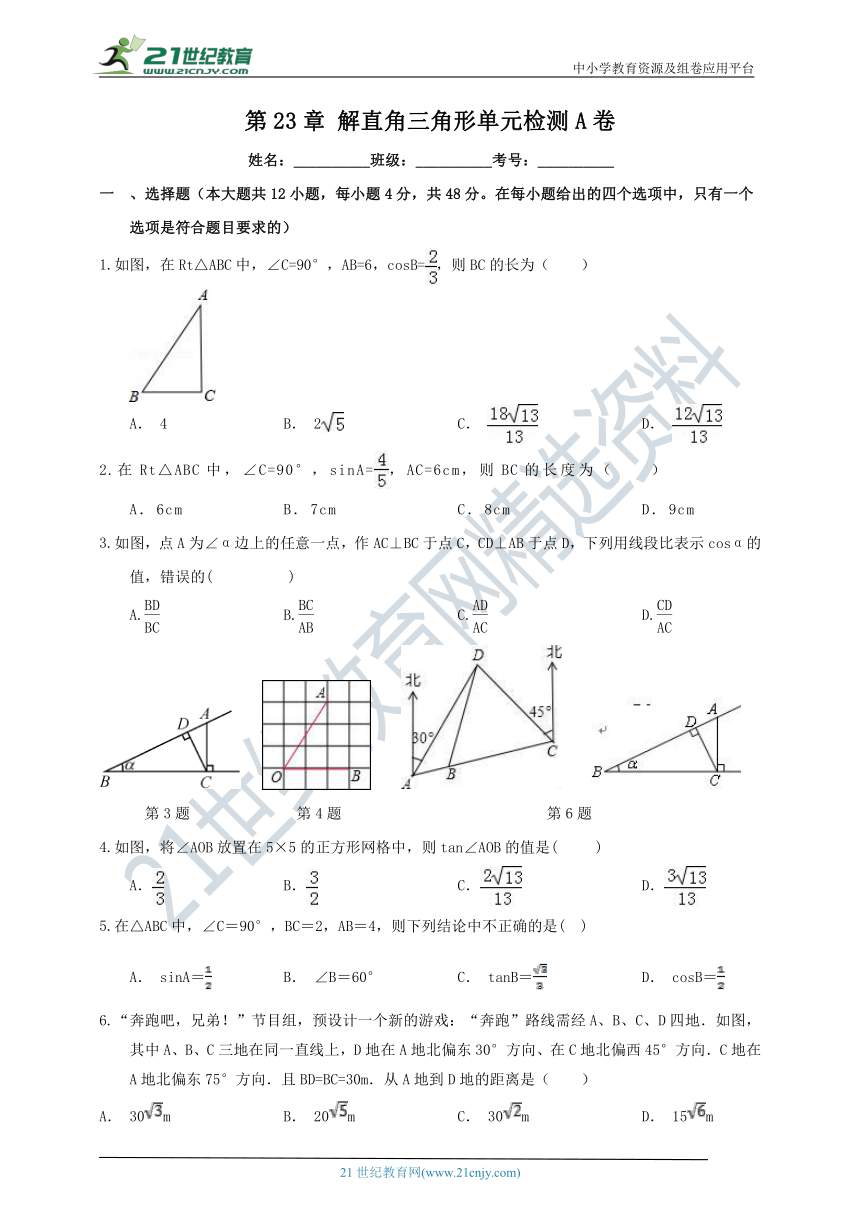
如图，在Rt△ABC中，∠C=90°，AB=6，cosB=，则BC的长为（　　）

A． 4 B． 2 C． D．
在Rt△ABC中，∠C=90°，sinA=，AC=6cm，则BC的长度为（　　）
A．6cm B．7cm C．8cm D．9cm
如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的( )

A. B. C. D.
如图，将∠AOB放置在5×5的正方形网格中，则tan∠AOB的值是( )

A． B． C． D．
在△ABC中，∠C＝90°，BC＝2，AB＝4，则下列结论中不正确的是( )
A． sinA＝ B． ∠B＝60° C． tanB＝ D． cosB＝
“奔跑吧，兄弟！”节目组，预设计一个新的游戏：“奔跑”路线需经A、B、C、D四地．如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C地在A地北偏东75°方向．且BD=BC=30m．从A地到D地的距离是（　　）

A． 30m B． 20m C． 30m D． 15m

如图，是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌．立杆AB的高度是米，从D点测得显示牌顶端C和底端B的仰角分别是60°和45°，则显示牌BC的高度为（ ）

A． 米 B． (3－)米 C． 9米 D． (2－3)米
某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（ ）．

A． 450a元 B． 225a元 C． 150a元 D． 300a元
如图所示，在△ABC中，∠C＝90°，AC＝16 cm，AB的垂直平分线MN交AC于D，连接BD，若，则BD的长是( )．

A． 4 cm B． 6 cm C． 8 cm D． 10 cm
在直角△ABC中，∠C=90°，∠A、∠B与∠C的对边分别是a、b和c，那么下列关系中，正确的是（　　）
A．cosA= B．tanA= C．sinA= D．cosA=
如图，在中，点在上，且，，若，则（ ）

A． B． C． D．
在△ABC中，AB=12，AC=13，cos∠B=，则BC边长为（　　）
A． 7 B． 8 C． 8或17 D． 7或17
二 、填空题（本大题共6小题，每小题4分，共24分）
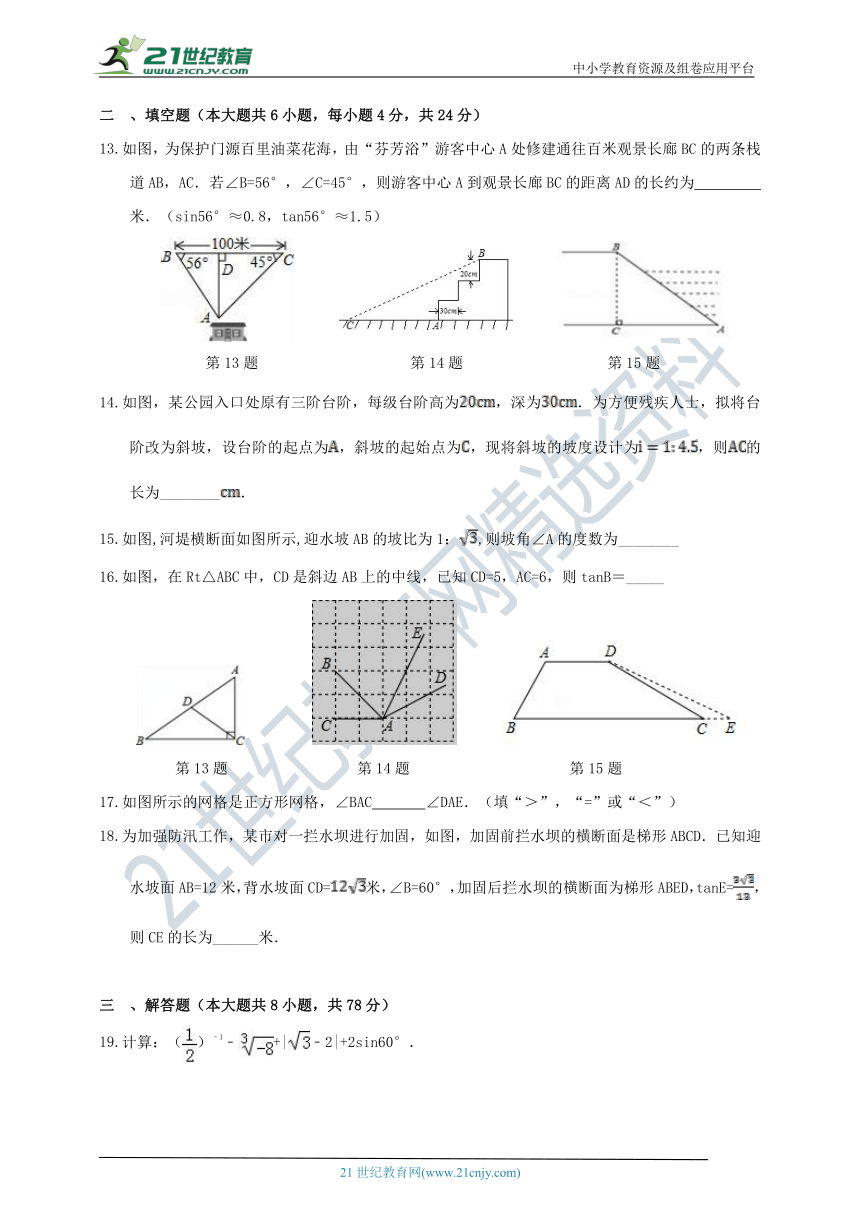
如图，为保护门源百里油菜花海，由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB，AC．若∠B=56°，∠C=45°，则游客中心A到观景长廊BC的距离AD的长约为　　　　　　米．（sin56°≈0.8，tan56°≈1.5）

如图，某公园入口处原有三阶台阶，每级台阶高为，深为．为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为，斜坡的起始点为，现将斜坡的坡度设计为，则的长为________．

如图,河堤横断面如图所示,迎水坡AB的坡比为1：,则坡角∠A的度数为________

如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tanB＝_____

如图所示的网格是正方形网格，∠BAC　 　∠DAE．（填“＞”，“=”或“＜”）

为加强防汛工作，某市对一拦水坝进行加固，如图，加固前拦水坝的横断面是梯形ABCD．已知迎水坡面AB=12米，背水坡面CD=米，∠B=60°，加固后拦水坝的横断面为梯形ABED，tanE=，则CE的长为______米．

三 、解答题（本大题共8小题，共78分）
计算：（）﹣1﹣+|﹣2|+2sin60°．
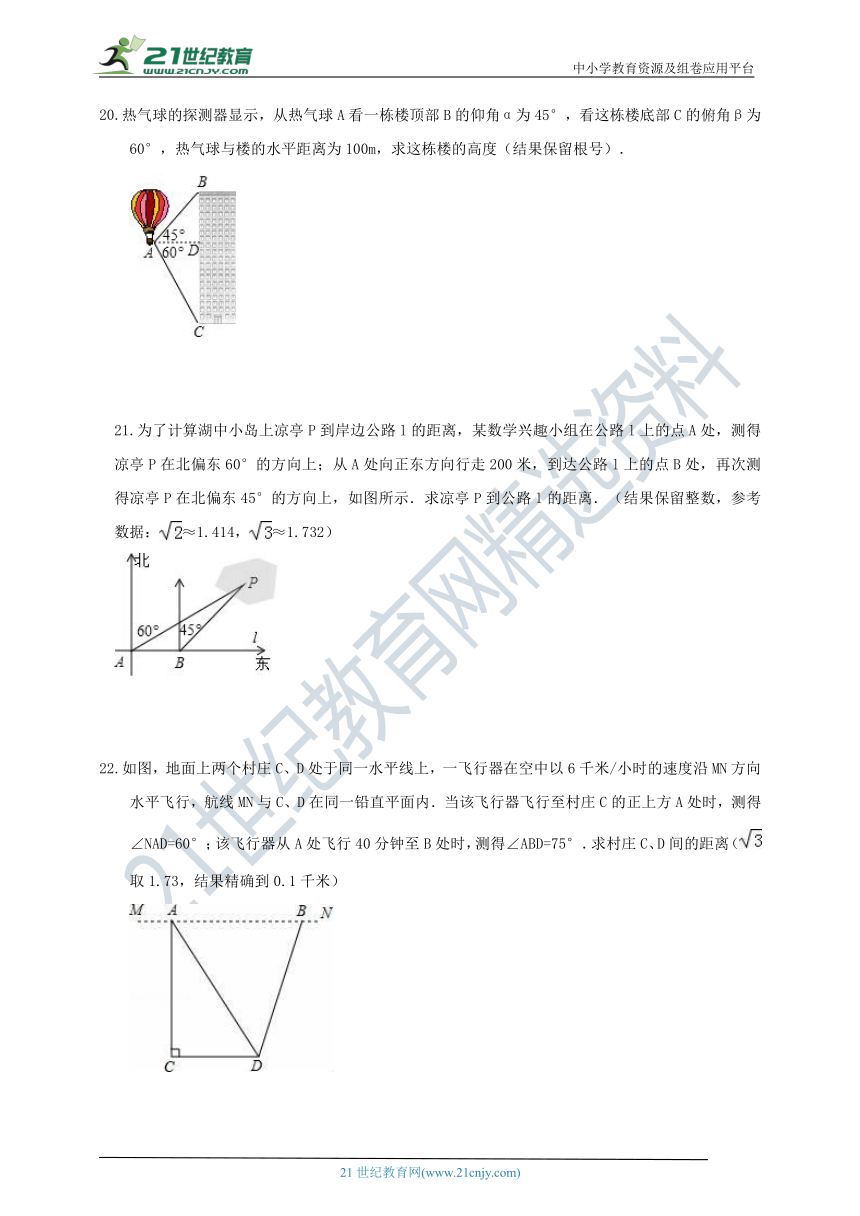
热气球的探测器显示，从热气球A看一栋楼顶部B的仰角α为45°，看这栋楼底部C的俯角β为60°，热气球与楼的水平距离为100m，求这栋楼的高度（结果保留根号）．

为了计算湖中小岛上凉亭P到岸边公路l的距离，某数学兴趣小组在公路l上的点A处，测得凉亭P在北偏东60°的方向上；从A处向正东方向行走200米，到达公路l上的点B处，再次测得凉亭P在北偏东45°的方向上，如图所示．求凉亭P到公路l的距离．（结果保留整数，参考数据：≈1.414，≈1.732）

如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以6千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内．当该飞行器飞行至村庄C的正上方A处时，测得∠NAD=60°；该飞行器从A处飞行40分钟至B处时，测得∠ABD=75°．求村庄C、D间的距离（取1.73，结果精确到0.1千米）

某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°．求路况指示牌DE的高度．（精确到0.01米）

A，B两地被大山阻隔，若要从A地到B地，只能沿着如图所示的公路先从A地到C地，再由C地到B地．现计划开凿隧道A，B两地直线贯通，经测量得：∠CAB=30°，∠CBA=45°，AC=20km，求隧道开通后与隧道开通前相比，从A地到B地的路程将缩短多少？（结果精确到0.1km，参考数据：≈1.414，≈1.732）

拉杆旅行箱为人们的出行带来了极大的方便，右图是一种拉杆旅行箱的侧面示意图，箱体ABCD可视为矩形，其中AB为50cm，BC为30cm，点A到地面的距离AE为4cm，旅行箱与水平面AF成60°角，求箱体的最高点C到地面的距离．

如图，在△ABC中，∠C=90°，AC=3，BC=4，点D，E分别在AC，BC上（点D与点A，C不重合），且∠DEC=∠A，将△DCE绕点D逆时针旋转90°得到△DC′E′．当△DC′E′的斜边、直角边与AB分别相交于点P，Q（点P与点Q不重合）时，设CD=x，PQ=y．
（1）求证：∠ADP=∠DEC；
（2）求y关于x的函数解析式，并直接写出自变量x的取值范围．



答案解析
一 、选择题
【考点】锐角三角函数的定义．
【分析】根据cosB=，可得=，再把AB的长代入可以计算出CB的长．
解：∵cosB=，
∴=，
∵AB=6，
∴CB=×6=4，
故选：A．
【点评】 此题主要考查了锐角三角函数的定义，关键是掌握余弦：锐角A的邻边b与斜边c的比叫做∠A的余弦．
【考点】解直角三角形．
【分析】根据三角函数的定义求得BC和AB的比值，设出BC、AB，然后利用勾股定理即可求解．
【解答】解：∵sinA==，
∴设BC=4x，AB=5x，
又∵AC2+BC2=AB2，
∴62+（4x）2=（5x）2，
解得：x=2或x=﹣2（舍），
则BC=4x=8cm，
故选：C．
【考点】锐角三角函数的定义
【分析】利用垂直的定义以及互余的定义得出∠α=∠ACD，进而利用锐角三角函数关系得出答案．
解：∵AC⊥BC，CD⊥AB，
∴∠α+∠BCD=∠ACD+∠BCD，
∴∠α=∠ACD，
∴cosα=cos∠ACD===，
只有选项C错误，符合题意．
故选：C．
【考点】锐角三角函数的定义．
【分析】认真读图，在以∠AOB的O为顶点的直角三角形里求tan∠AOB的值．
解：由图可得tan∠AOB=．
故选B．
【点评】本题考查了锐角三角函数的概念：在直角三角形中，正切等于对边比邻边．
【考点】三角函数锐角-正弦，余弦，正切
【分析】先根据勾股定理求出的长，再根据锐角三角函数的定义进行计算即可.
解： 中，，，，
，
、，故此选项正确，不符合题意；
、，则，故此选项正确，不符合题意；
、因为，所以，故此选项错误，符合题意；
、因为，所以，故此选项正确，不符合题意.
故选：.
【点睛】本题考查了锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比斜边.
【考点】解直角三角形的应用﹣方向角问题
【分析】过点D作DH垂直于AC，垂足为H，求出∠DAC的度数，判断出△BCD是等边三角形，再
利用三角函数求出AB的长，从而得到AB+BC+CD的长．
解：过点D作DH垂直于AC，垂足为H，
由题意可知∠DAC=75°﹣30°=45°．
∵△BCD是等边三角形，
∴∠DBC=60°，BD=BC=CD=30m，
∴DH=×30=15，
∴AD=DH=15m．
故从A地到D地的距离是15m．
故选D．

【点睛】本题考查了解直角三角形的应用﹣﹣方向角问题，结合航海中的实际问题，将解直角三
角形的相关知识有机结合，体现了数学应用于实际生活的思想．
【考点】锐角三角函数定义
【分析】先推出AD=AB=，利用三角函数在直角三角形ACD中求AC，再得BC=AC-AB=3-（米）
解：∵∠BAD=90°, ∠ADB=45°,
∴AD=AB=
又∵∠ADC=60°,
∴AC=AD?tan∠ADC=×=3,
∴BC=AC-AB=3-（米）
故选：B
【点睛】本题考核知识点：解直角三角形. 解题关键点：熟记特殊角的三角函数值.
【考点】解直角三角形的应用﹣坡度坡角问题
【分析】求出三角形地的面积即可求解．如图所示，作BD⊥CA于D点．在Rt△ABD中，利用正弦函数定义求BD，即△ABC的高．运用三角形面积公式计算面积求解．
解：如图所示，作BD⊥CA于D点,

∵
∴ ，
∵AB=20米，
∴ 米，
∴(米2).
已知这种草皮每平方米a元，
所以一共需要150a元.
故选:C.
【点睛】考查解直角三角形的应用，作出辅助线，根据锐角三角函数求出高是解题的关键.
【考点】锐角三角函数
【分析】根据线段垂直平分线的性质可得BD＝AD，已知，设DC＝3k，则BD＝5k，即可得AD＝5k，AC＝8k．由此求得k值，即可求得BD的长.
解：∵ MN是AB的中垂线,
∴ BD＝AD．
又，
设DC＝3k，则BD＝5k，
∴ AD＝5k，AC＝8k．
∴8k＝16，k＝2，
∴BD＝5×2＝10cm．
故选D.
【点睛】本题考查了线段垂直平分线的性质及解直角三角形的相关知识，综合性较强，计算要仔细．
【考点】锐角三角函数的定义．
【分析】根据三角函数定义：（1）正弦：我们把锐角A的对边a与斜边c的比叫做∠A的正弦，记作sinA．
（2）余弦：锐角A的邻边b与斜边c的比叫做∠A的余弦，记作cosA．
（3）正切：锐角A的对边a与邻边b的比叫做∠A的正切，记作tanA．分别进行分析即可．
解：在直角△ABC中，∠C=90°，则
A、cosA=，故本选项错误；
B、tanA=，故本选项错误；
C、sinA=，故本选项正确；
D、cosA=，故本选项错误；
故选：C．

【点评】此题主要考查了锐角三角函数的定义，关键是熟练掌握锐角三角函数的定义．
【考点】锐角三角函数定义，相似三角形的判定和性质
解：作DE⊥AD,交AC于点E，如图所示：

∵DE⊥AD、AB⊥AD，
∴AB//DE（垂直同一条直线的两直线平行），
∴∠BAC＝、∠B＝∠CDE（两直线平行，同位角相等），
在和中，
，
∴∽（AAA），
∴，
又∵（已知），
∴，
∴
设AD＝4x，
∵(已知),
∴AB＝3x,AD=4x,
又∵（已证），
∴DE＝x,
在直角，＝，
∴tan∠CAD=
故选B。
【点睛】求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中，若所求三角函数的角不在直角三角形中时，则需通过作辅助线构造直角三角形，再根据题意求两边的长度或比值即可。
【考点】 解直角三角形
【分析】 首先根据特殊角的三角函数值求得∠B的度数，然后分锐角三角形和钝角三角形分别求得BD和CD的长后即可求得线段BC的长．
解：∵cos∠B=，
∴∠B=45°，
当△ABC为钝角三角形时，如图1，
∵AB=12，∠B=45°，
∴AD=BD=12，
∵AC=13，
∴由勾股定理得CD=5，
∴BC=BD﹣CD=12﹣5=7；
当△ABC为锐角三角形时，如图2，
BC=BD+CD=12+5=17，
故选D．

【点评】本题考查了解直角三角形的知识，能从中整理出直角三角形是解答本题的关键，难点为分类讨论，难点中等．
二 、填空题
【考点】解直角三角形的应用．
【分析】根据题意和图形可以分别表示出AD和CD的长，从而可以求得AD的长，本题得以解决．
解：∵∠B=56°，∠C=45°，∠ADB=∠ADC=90°，BC=BD+CD=100米，
∴BD=，CD=，
∴+=100，
解得，AD≈60，
故答案为：60．
【考点】解直角三角形的应用﹣坡度坡角问题
【分析】如图所示，所有台阶高度和为BD的长，所有台阶深度和为AD的长，即BD＝60cm，AD＝60cm，然后根据坡度比解答.
解：由图可知：B＝60cm，AD＝60cm，∵坡度比＝BD∶DC＝1∶4.5，∴DC＝270，∴AC＝DC－AD＝270－60＝210cm.

【点睛】本题考查运用所学的解直角三角形的知识解决实际生活中的问题，要求我们要具备数学建模能力（即将实际问题转换为数学问题）.
【考点】解直角三角形的应用﹣坡度坡角问题
【分析】根据坡角的定义，tanA==1：=,可得∠A.
解：因为，tanA==1：=,
所以，∠A =30,
故答案为：30
【点睛】本题考核知识点：正切的应用. 解题关键点：理解坡角的意义.
【考点】锐角三角函数定义，直角三角形斜边上的中线，勾股定理
解：在Rt△ABC中， CD是斜边AB上的中线, CD=5
∴AB=2CD=10
依据勾股定理可得，

故答案为：
【点睛】在直角三角形中，斜边的中线等于斜边的一半.首先由这个性质得出斜边的长是这个题目解题的关键.由勾股定理得出这个直角三角形的另一条直角边，再依据锐角三角函数得出正切值.
【考点】锐角三角函数的增减性
【分析】作辅助线，构建三角形及高线NP，先利用面积法求高线PN=，再分别求∠BAC、∠DAE的正弦，根据正弦值随着角度的增大而增大，作判断．
解：连接NH，BC，过N作NP⊥AD于P，
S△ANH=2×2﹣﹣×1×1=AH?NP，
=PN，
PN=，
Rt△ANP中，sin∠NAP====0.6，
Rt△ABC中，sin∠BAC===＞0.6，
∵正弦值随着角度的增大而增大，
∴∠BAC＞∠DAE，
故答案为：＞．

【点评】本题考查了锐角三角函数的增减性，构建直角三角形求角的三角函数值进行判断，熟练掌握锐角三角函数的增减性是关键．
【考点】解直角三角形的应用﹣坡度坡角问题
【分析】分别过A、D作AF⊥BC于点F，DG⊥BC于点G．在Rt△ABF中，求得AF的值，又DG=AF求得DG.在Rt△CDG中，求出CG的长，再在Rt△DEG中，根据tanE＝得到GE的长，根据CE=GE-CG即可求解．
解：分别过A、D作AF⊥BC于点F，DG⊥BC于点G．
在Rt△ABF中，AB=12米，∠B=60°，
∴sin∠B=，
∴AF=12×=6.
易知四边形AFGD是矩形，
∴DG=AF=6.
在Rt△DGC中，CD=12，DG=6，
∴GC==18.
在Rt△DEG中，tanE＝= ，
∴EG=26，
∴CE=GE-CG=26-18=8．
故答案为8．
三 、解答题
【考点】负指数幂的性质，绝对值的性质，特殊角的三角函数值
【分析】接利用负指数幂的性质以及绝对值的性质以及特殊角的三角函数值、立方根的性质分别化简得出答案．
解：原式=2+2+2﹣+2×
=6﹣+
=6．
【点评】此题主要考查了实数运算，正确化简各数是解题关键．
【考点】解直角三角形的应用﹣仰角俯角问题．
【分析】根据正切的概念分别求出BD、DC，计算即可．
解：在Rt△ADB中，∠BAD=45°，
∴BD=AD=100m，
在Rt△ADC中，CD=AD×tan∠DAC=100m
∴BC=（100+100）m，
答：这栋楼的高度为（100+100）m．
【考点】解直角三角形的应用-方向角
【分析】作PD⊥AB于D，构造出Rt△APD与Rt△BPD，根据AB的长度．利用特殊角的三角函数值求解．
解：作PD⊥AB于D．

设BD=x，则AD=x+200．
∵∠EAP=60°，
∴∠PAB=90°﹣60°=30°．
在Rt△BPD中，
∵∠FBP=45°，
∴∠PBD=∠BPD=45°，
∴PD=DB=x．
在Rt△APD中，
∵∠PAB=30°，
∴CD=tan30°?AD，
即DB=CD=tan30°?AD=x=（200+x），
解得：x≈273.2，
∴CD=273.2．
答：凉亭P到公路l的距离为273.2m．
【点评】此题考查的是直角三角形的性质，解答此题的关键是构造出两个特殊角度的直角三角形，再利用特殊角的三角函数值解答．
【考点】解直角三角形的应用．
【分析】过B作BE⊥AD于E，三角形的内角和得到∠ADB=45°，根据直角三角形的性质得到AE=2．BE=2，求得AD=2+2，即可得到结论．
解：过B作BE⊥AD于E，
∵∠NAD=60°，∠ABD=75°，
∴∠ADB=45°，
∵AB=6×=4，
∴AE=2．BE=2，
∴DE=BE=2，
∴AD=2+2，
∵∠C=90，∠CAD=30°，
∴CD=AD=1+．

【考点】解直角三角形的应用-仰角俯角问题．
【分析】过点A作AF⊥DC于点F，在Rt△ADF中求出DF，在Rt△AEF中求出EF，继而根据DE=DF﹣EF，可得出答案．
解：过点A作AF⊥DC于点F，

在Rt△ADF中，AF=3.2m，tan∠DAF=tan52°=，
则DF=AFtan52°=3.2×1.28≈4.10米．
在Rt△AEF中，AF=3.2m，tan∠EAF=tan32°=，
则DF=AFtan32°=3.2×0.62≈2.00米．
故可得DE=DF﹣EF=2.10米．
答：路况指示牌DE的高度为2.10米．
【点评】本题考查了解直角三角形的应用，要求学生能借助仰角构造直角三角形并解直角三角形，难度一般．
【考点】解直角三角形的应用．
【分析】过点C作CD⊥AB与D，根据AC=20km，∠CAB=30°，求出CD、AD，根据∠CBA=45°，求出BD、BC，最后根据AB=AD+BD列式计算即可．
解：过点C作CD⊥AB与D，
∵AC=20km，∠CAB=30°，
∴CD=AC=×20=10km，
AD=cos∠CAB?AC=cos∠30°×20=10km，
∵∠CBA=45°，
∴BD=CD=10km，BC=CD=10≈14.14km
∴AB=AD+BD=10+10≈27.32km．
则AC+BC﹣AB≈20+14.14﹣27.32≈6.8km．
答：从A地到B地的路程将缩短6.8km．

【考点】 解直角三角形的应用．
【分析】 如图，过点B、A分别作地面的平行线a、b．过C作CM⊥a于点M，过点B作BN⊥b于点N．在直角△BCM、△ABN中利用三角函数分别求得CM、BN的长，则点C到地面的高度是：CM+BN+AE．
解：如图，过点B、A分别作地面的平行线a、b．过C作CM⊥a于点M，过点B作BN⊥b于点N．
在直角△ABN中，AB=50cm，∠BAN=60°，则BN=AB?sin60°=25cm．
在直角△BCM中，易求∠CBM=30°，则CM=BC=15cm．
所以，点C到地面的高度是：CM+BN+AE=15+25+4=19+25（cm）．
答：箱体的最高点C到地面的距离是（19+25）cm．

【点评】 此题考查了三角函数的基本概念，主要是正弦概念及运算，关键把实际问题转化为数学问题加以计算．
【考点】旋转的性质；函数关系式；矩形的判定与性质；解直角三角形．
【分析】（1）根据等角的余角相等即可证明；
（2）分两种情形①如图1中，当C′E′与AB相交于Q时，即＜x≤时，过P作MN∥DC′，设∠B=α．②当DC′交AB于Q时，即＜x＜3时，如图2中，作PM⊥AC于M，PN⊥DQ于N，则四边形PMDN是矩形，分别求解即可；
（1）证明：如图1中，

∵∠EDE′=∠C=90°，
∴∠ADP+∠CDE=90°，∠CDE+∠DEC=90°，
∴∠ADP=∠DEC．
（2）解：如图1中，当C′E′与AB相交于Q时，即＜x≤时，过P作MN∥DC′，设∠B=α
∴MN⊥AC，四边形DC′MN是矩形，
∴PM=PQ?cosα=y，PN=×（3﹣x），
∴（3﹣x）+y=x，
∴y=x﹣，
当DC′交AB于Q时，即＜x＜3时，如图2中，作PM⊥AC于M，PN⊥DQ于N，则四边形PMDN是矩形，

∴PN=DM，
∵DM=（3﹣x），PN=PQ?sinα=y，
∴（3﹣x）=y，
∴y=﹣x+．
综上所述，y=






















































21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)