第四章 图形的平移与旋转 第1课时(练习)
文档属性
| 名称 | 第四章 图形的平移与旋转 第1课时(练习) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-02 17:40:28 | ||
图片预览

文档简介
第四章 图形的平移与旋转
1 图形的平移
第1课时 平移的性质
自主预习
1.平移:在平面内,将一个图形沿某个_____________移动一定的_____________,图形的这种变化称为平移。
2.平移的性质:一个图形和它经过平移所得的图形中,对应点所连的线段_______________(或在同一条直线上)且___________ ___;对应线段________ _______(或在同条直线上)且______ ______,对应角____________。
课堂巩固
知识点一:平移的定义
1.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤中哪一个图案可以通过平移图案①得到( )
A.② B.③ C.④ D.⑤
2.如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A.向右平移1格,向下平移3格
B.向右平移1格,向下平移4格
C.向右平移2格,向下平移4格
D.向右平移2格,向下平移3格
3.下面生活中的物体的运动情况可以看成平移的是_____________(填写序号即可)。
①摆动的钟摆;②在笔直的公路上行驶的汽车;③随风摆动的旗帜;④摇动的大绳;⑤汽车玻璃上雨刷的运动。
知识点二:平移的性质
4.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
6 B. 8 C. 10 D.12
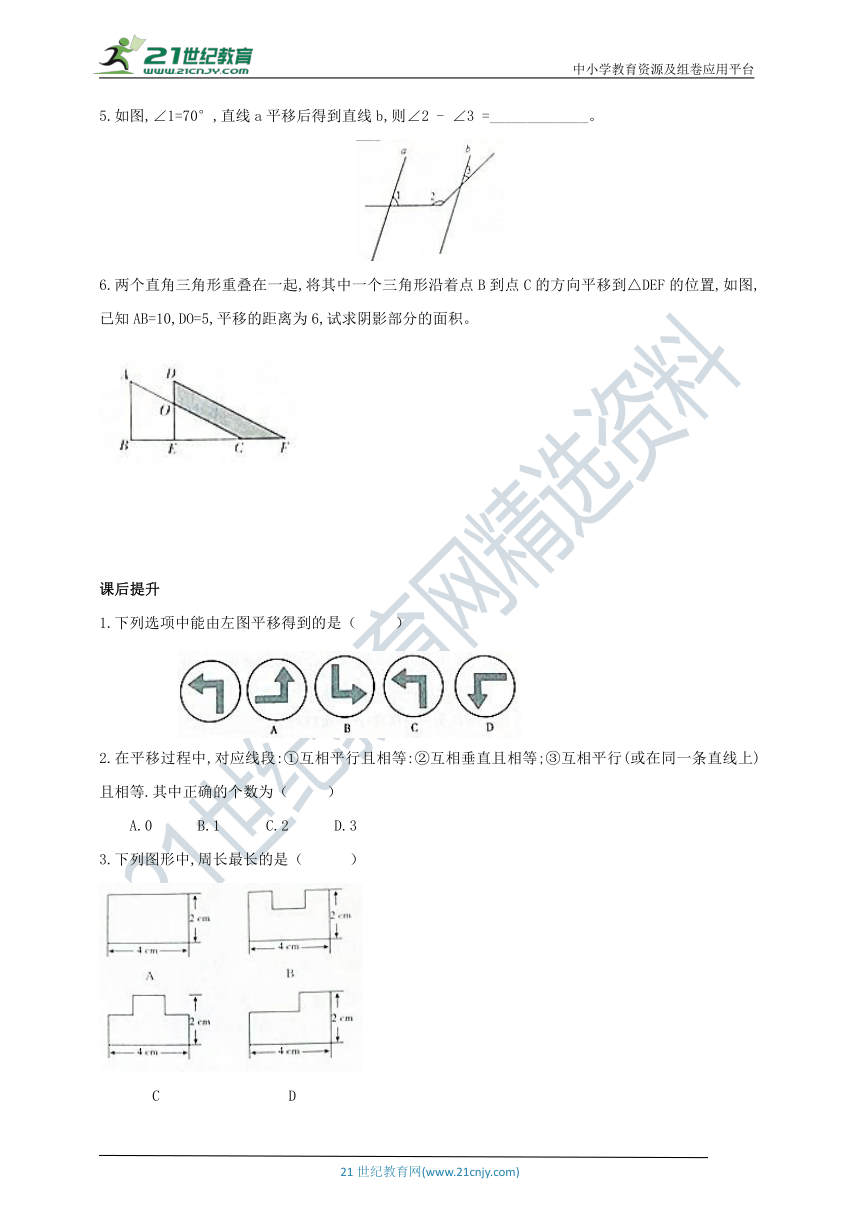
5.如图,∠1=70°,直线a平移后得到直线b,则∠2 - ∠3 =_____________。
6.两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,如图,已知AB=10,DO=5,平移的距离为6,试求阴影部分的面积。
课后提升
1.下列选项中能由左图平移得到的是( )
2.在平移过程中,对应线段:①互相平行且相等:②互相垂直且相等;③互相平行(或在同一条直线上)且相等.其中正确的个数为( )
A.0 B.1 C.2 D.3
3.下列图形中,周长最长的是( )
C D
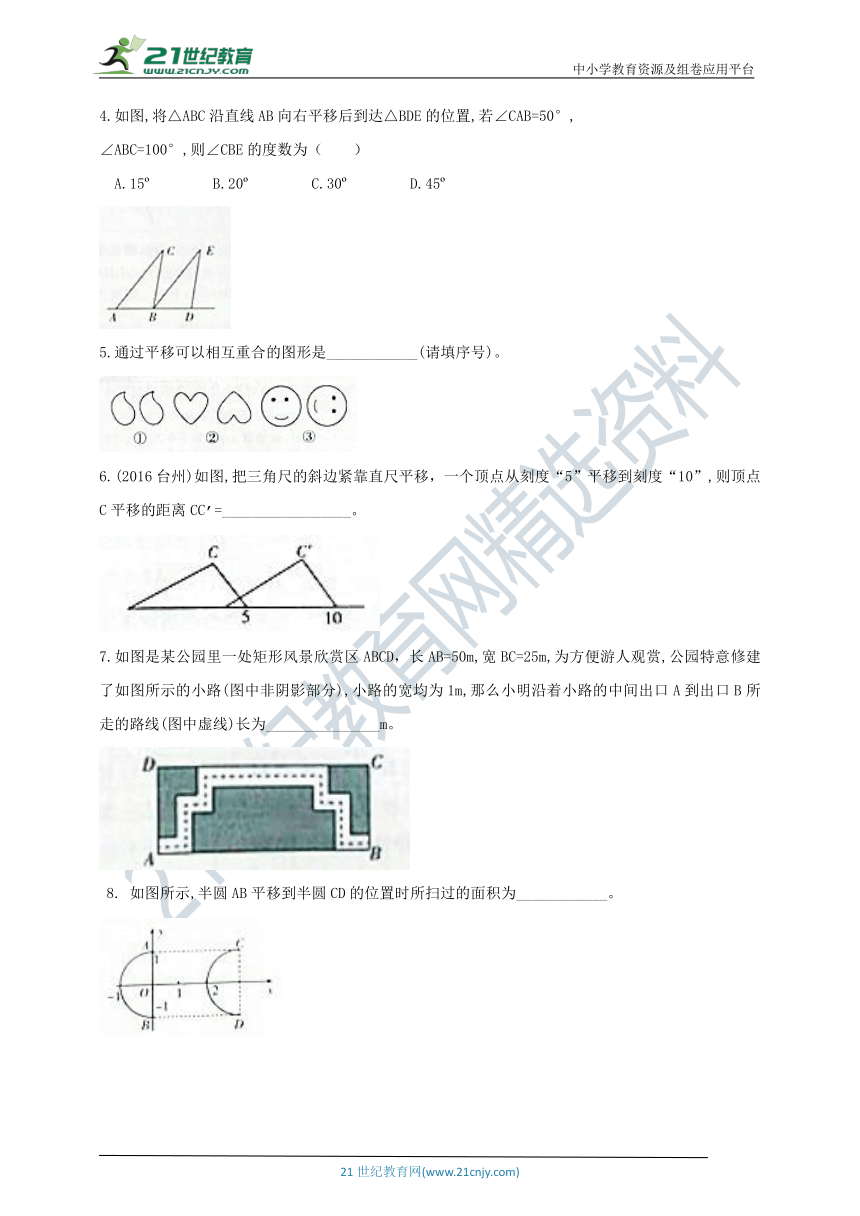
4.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,
∠ABC=100°,则∠CBE的度数为( )
A.15o B.20o C.30o D.45o
5.通过平移可以相互重合的图形是____________(请填序号)。
6.(2016台州)如图,把三角尺的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC’=_________________。
7.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50m,宽BC=25m,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为_______________m。
如图所示,半圆AB平移到半圆CD的位置时所扫过的面积为____________。
9.某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3m,其剖面如图所示,请你
计算一下:
(1)铺此楼梯,需要购买地毯的长是多少?
(2)需购买的地毯面积是多少?
素养锤炼
在长方形地块上建造公共绿地(图中阴影部分),其余的部分是小路.根据图中的设计方案,利用你所学习的有关图形运动的知识,解决下列问题:
(1)用含有x的代数式表示出公共绿地的面积;
(2)当x=1时,计算出绿地的面积。
参考答案及解析
自主预习
1.方向 距离 2.平行 相等 平行 相等 相等
课堂巩固
1.D 2.C 3.② 4.C 5.110
6.解:由平移的性质知,BE=6,DE=AB=10,∴OE=DE-DO=10-5=5,
∴S四边形ODFC=S梯形ABEO=(AB+OE)·BE=(10+5)×6=45。
课后提升
1.C 2.B 3.B 4.C 5.① 6. 5 7.98 8.6
9.解:(1)2.4+1.2=3.6(m)
答:地毯总长为3.6m.
(2)3.6×3=10.8(m2)
答:需购买的地毯面积是10.8m2。
素养锤炼
解:(1)由题意得,通过平移,绿地部分可以拼成一个矩形,它的长为50-2x、宽为30-x.
∴面积为(50-2x)(30-x)=2x2-110x+1500,故公共绿地的面积为2x2-110x+1500;
(2)当x=1时,绿地的面积=2-110+1500=1392。
1 图形的平移
第1课时 平移的性质
自主预习
1.平移:在平面内,将一个图形沿某个_____________移动一定的_____________,图形的这种变化称为平移。
2.平移的性质:一个图形和它经过平移所得的图形中,对应点所连的线段_______________(或在同一条直线上)且___________ ___;对应线段________ _______(或在同条直线上)且______ ______,对应角____________。
课堂巩固
知识点一:平移的定义
1.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤中哪一个图案可以通过平移图案①得到( )
A.② B.③ C.④ D.⑤
2.如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A.向右平移1格,向下平移3格
B.向右平移1格,向下平移4格
C.向右平移2格,向下平移4格
D.向右平移2格,向下平移3格
3.下面生活中的物体的运动情况可以看成平移的是_____________(填写序号即可)。
①摆动的钟摆;②在笔直的公路上行驶的汽车;③随风摆动的旗帜;④摇动的大绳;⑤汽车玻璃上雨刷的运动。
知识点二:平移的性质
4.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
6 B. 8 C. 10 D.12
5.如图,∠1=70°,直线a平移后得到直线b,则∠2 - ∠3 =_____________。
6.两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,如图,已知AB=10,DO=5,平移的距离为6,试求阴影部分的面积。
课后提升
1.下列选项中能由左图平移得到的是( )
2.在平移过程中,对应线段:①互相平行且相等:②互相垂直且相等;③互相平行(或在同一条直线上)且相等.其中正确的个数为( )
A.0 B.1 C.2 D.3
3.下列图形中,周长最长的是( )
C D
4.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,
∠ABC=100°,则∠CBE的度数为( )
A.15o B.20o C.30o D.45o
5.通过平移可以相互重合的图形是____________(请填序号)。
6.(2016台州)如图,把三角尺的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC’=_________________。
7.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50m,宽BC=25m,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为_______________m。
如图所示,半圆AB平移到半圆CD的位置时所扫过的面积为____________。
9.某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3m,其剖面如图所示,请你
计算一下:
(1)铺此楼梯,需要购买地毯的长是多少?
(2)需购买的地毯面积是多少?
素养锤炼
在长方形地块上建造公共绿地(图中阴影部分),其余的部分是小路.根据图中的设计方案,利用你所学习的有关图形运动的知识,解决下列问题:
(1)用含有x的代数式表示出公共绿地的面积;
(2)当x=1时,计算出绿地的面积。
参考答案及解析
自主预习
1.方向 距离 2.平行 相等 平行 相等 相等
课堂巩固
1.D 2.C 3.② 4.C 5.110
6.解:由平移的性质知,BE=6,DE=AB=10,∴OE=DE-DO=10-5=5,
∴S四边形ODFC=S梯形ABEO=(AB+OE)·BE=(10+5)×6=45。
课后提升
1.C 2.B 3.B 4.C 5.① 6. 5 7.98 8.6
9.解:(1)2.4+1.2=3.6(m)
答:地毯总长为3.6m.
(2)3.6×3=10.8(m2)
答:需购买的地毯面积是10.8m2。
素养锤炼
解:(1)由题意得,通过平移,绿地部分可以拼成一个矩形,它的长为50-2x、宽为30-x.
∴面积为(50-2x)(30-x)=2x2-110x+1500,故公共绿地的面积为2x2-110x+1500;
(2)当x=1时,绿地的面积=2-110+1500=1392。
