北师大版九年级数学上册第五章第2节视图课件(共41张PPT)
文档属性
| 名称 | 北师大版九年级数学上册第五章第2节视图课件(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-03 00:00:00 | ||
图片预览








文档简介
投影
平行投影
中心投影
正投影
斜投影
请观察下面三个投影,它们有什么相同与不同的地方?你能试着给正投影下定义吗?
三视图
三视图的形成
物体向投影面投影所得到的图形称为视图。
如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。
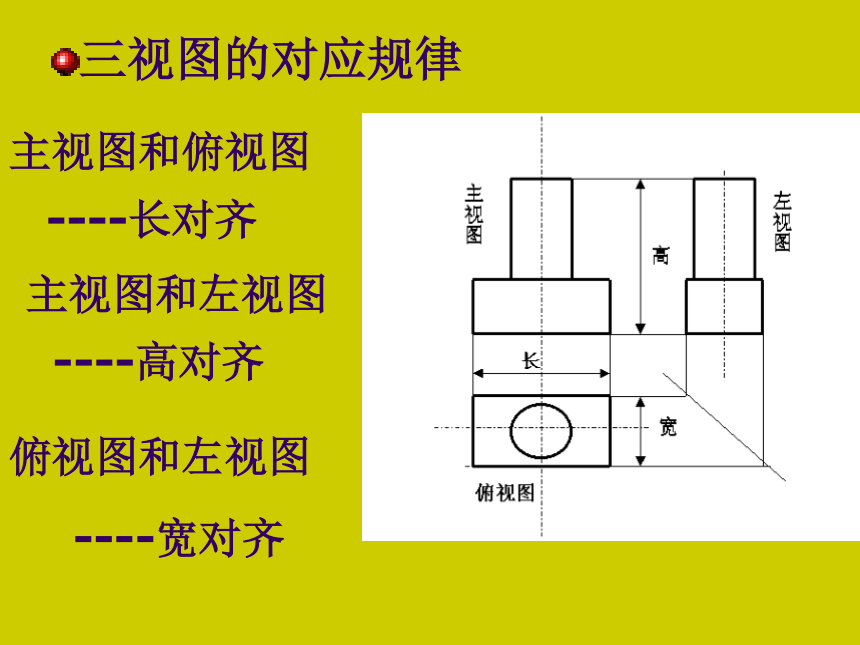
三视图的对应规律
俯视图和左视图
主视图和俯视图
主视图和左视图
----长对齐
----高对齐
----宽对齐
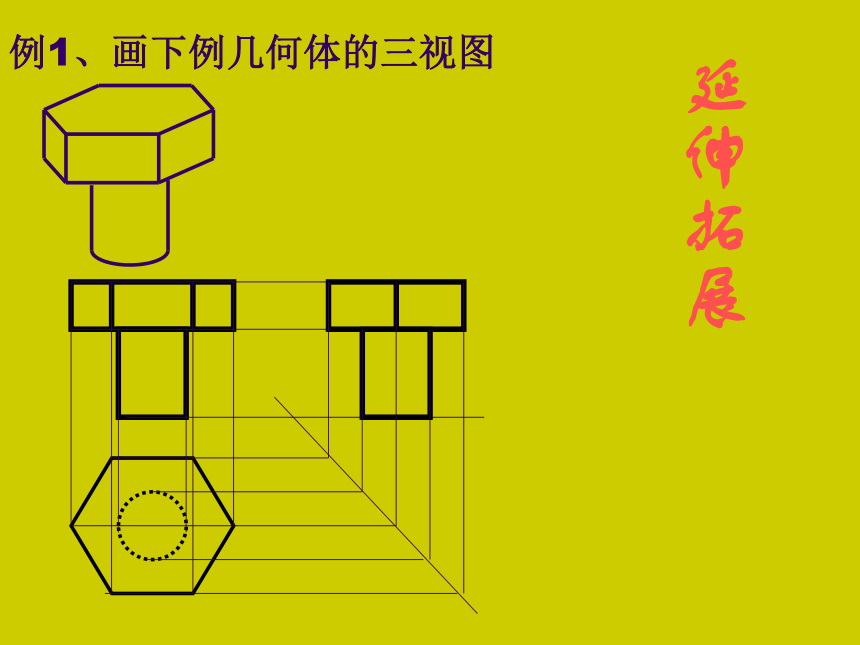
例1、画下例几何体的三视图
延伸拓展
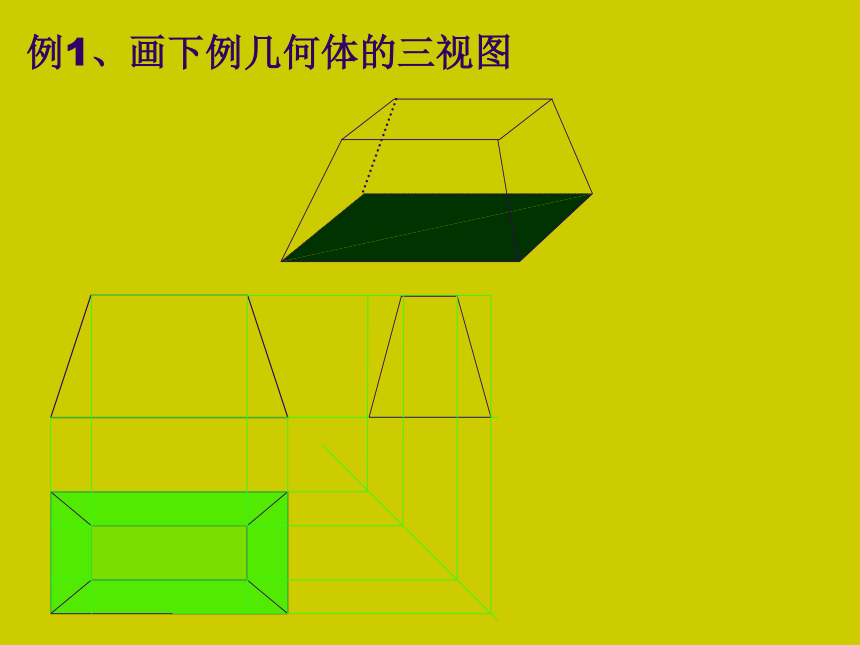
例1、画下例几何体的三视图
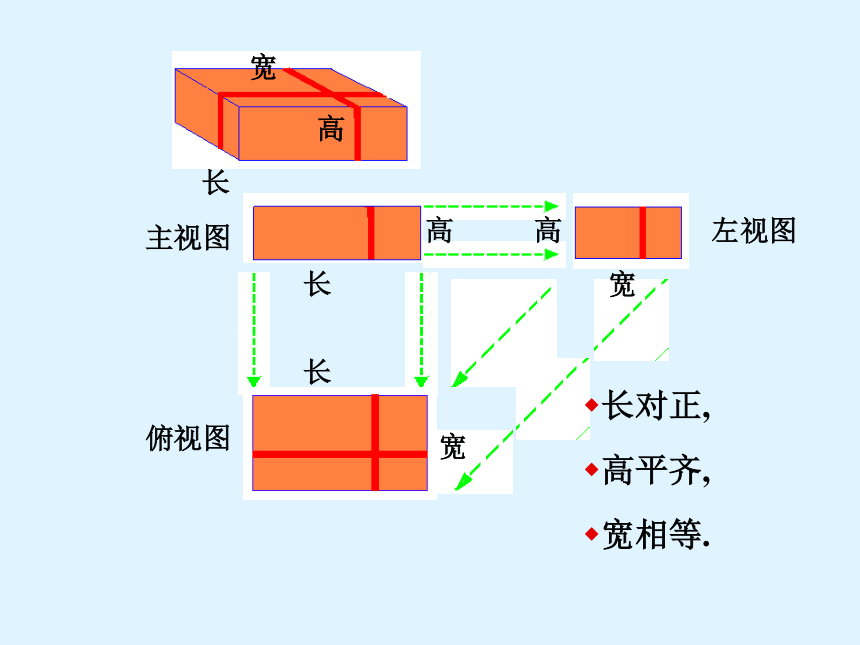
长对正,
高平齐,
宽相等.
回味无穷
三视图
主视图——从正面看到的图
左视图——从左面实物的三视图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
你能想象出下面各几何体的主视图,左视图,俯视图吗?
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
三视图
主视图
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
主视图
左视图
俯视图
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
根据如图右边的椅子的视图,工人就能制造出符合设计要求的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广泛的应用.
下面所给的三视图表示什么几何体?
直四棱柱
下面所给的三视图表示什么几何体?
直五棱柱
下面所给的三视图表示什么几何体?
圆锥
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
三棱锥
下面是一个物体的三视图,试说出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
俯视图
左视图
探究
根据三视图摆出它的立体图形
主视图
左视图
俯视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
主视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭救法(你可以用实物模型动手试一试)?你能用三视图表示你探究的结果吗?
图3-25
用小方块搭一个几何体,使得它的主视图和俯视图如图所示:
请你摆一摆,你会发现些什么?
做一做:由几个相同的小立方块搭成的几何体的俯视图如图所示。方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图。
⒉由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
由三视图描述几何体(或实物原型),一般先根据各视图想像从各个方向看到的几何体形状, 然后综合起来确定几何体(或实物原型)的形状, 再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢?
已知一个几何体的三视图如图3-23所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2)
图3-23
图3-24
1.某两个物体的三视图如图所示.请分别说出它们的形状.
正四棱锥
直三棱柱
2.由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
3.一个几何体的三个视图都是全等的正方形, 则这个几何体是______.
4.一个几何体的三视图都是半径相等的圆,则这个几何体是_______.
5.一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.
6.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(第5题)
(第6题)
立方体
球
直五棱柱,底面是五边形
直三棱柱
用小立方块搭一个几何体,使得它的主视图入土所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试。
动手实践
画三视图是培养空间想象力的一个重要途径.
在挑战自我的平台(由物体画三视图,反过来由三视图想象实物的形状)充分展现自我才华.
平行投影
中心投影
正投影
斜投影
请观察下面三个投影,它们有什么相同与不同的地方?你能试着给正投影下定义吗?
三视图
三视图的形成
物体向投影面投影所得到的图形称为视图。
如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。
三视图的对应规律
俯视图和左视图
主视图和俯视图
主视图和左视图
----长对齐
----高对齐
----宽对齐
例1、画下例几何体的三视图
延伸拓展
例1、画下例几何体的三视图
长对正,
高平齐,
宽相等.
回味无穷
三视图
主视图——从正面看到的图
左视图——从左面实物的三视图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
挑战“自我”,提高画三视图的能力.
你能想象出下面各几何体的主视图,左视图,俯视图吗?
实物的三视图
正三棱柱 四棱柱
你能画出它们主视图,左视图,俯视图吗?
三视图
主视图
俯视图
左视图
老师提示:
在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画三视图要认真准确,特别是宽相等.
主视图
左视图
俯视图
“做一做”
已知俯视图,画出它的主视图,左视图.
下图是底面为等腰直角三角形和等腰梯形的
三棱柱,四棱柱的俯视图,尝试画出它的主视图
和左视图,并与同伴交流.
根据如图右边的椅子的视图,工人就能制造出符合设计要求的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广泛的应用.
下面所给的三视图表示什么几何体?
直四棱柱
下面所给的三视图表示什么几何体?
直五棱柱
下面所给的三视图表示什么几何体?
圆锥
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
三棱锥
下面是一个物体的三视图,试说出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
下列是一个物体的三视图,请描述出它的形状
主视图
俯视图
左视图
探究
根据三视图摆出它的立体图形
主视图
左视图
俯视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
主视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭救法(你可以用实物模型动手试一试)?你能用三视图表示你探究的结果吗?
图3-25
用小方块搭一个几何体,使得它的主视图和俯视图如图所示:
请你摆一摆,你会发现些什么?
做一做:由几个相同的小立方块搭成的几何体的俯视图如图所示。方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图。
⒉由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
由三视图描述几何体(或实物原型),一般先根据各视图想像从各个方向看到的几何体形状, 然后综合起来确定几何体(或实物原型)的形状, 再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢?
已知一个几何体的三视图如图3-23所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2)
图3-23
图3-24
1.某两个物体的三视图如图所示.请分别说出它们的形状.
正四棱锥
直三棱柱
2.由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
3.一个几何体的三个视图都是全等的正方形, 则这个几何体是______.
4.一个几何体的三视图都是半径相等的圆,则这个几何体是_______.
5.一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.
6.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(第5题)
(第6题)
立方体
球
直五棱柱,底面是五边形
直三棱柱
用小立方块搭一个几何体,使得它的主视图入土所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试。
动手实践
画三视图是培养空间想象力的一个重要途径.
在挑战自我的平台(由物体画三视图,反过来由三视图想象实物的形状)充分展现自我才华.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
