2018-2019学年九年级数学下册单元测试(二)圆(b卷)(含答案)
文档属性
| 名称 | 2018-2019学年九年级数学下册单元测试(二)圆(b卷)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 171.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-02 00:00:00 | ||
图片预览

文档简介
单元测试(二) 圆(B卷)
一、选择题(每小题3分,共30分)
1.下列说法正确的是(B)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(C)
A.点P在⊙O上 B.点P在⊙O内
C.点P在⊙O外 D.无法确定
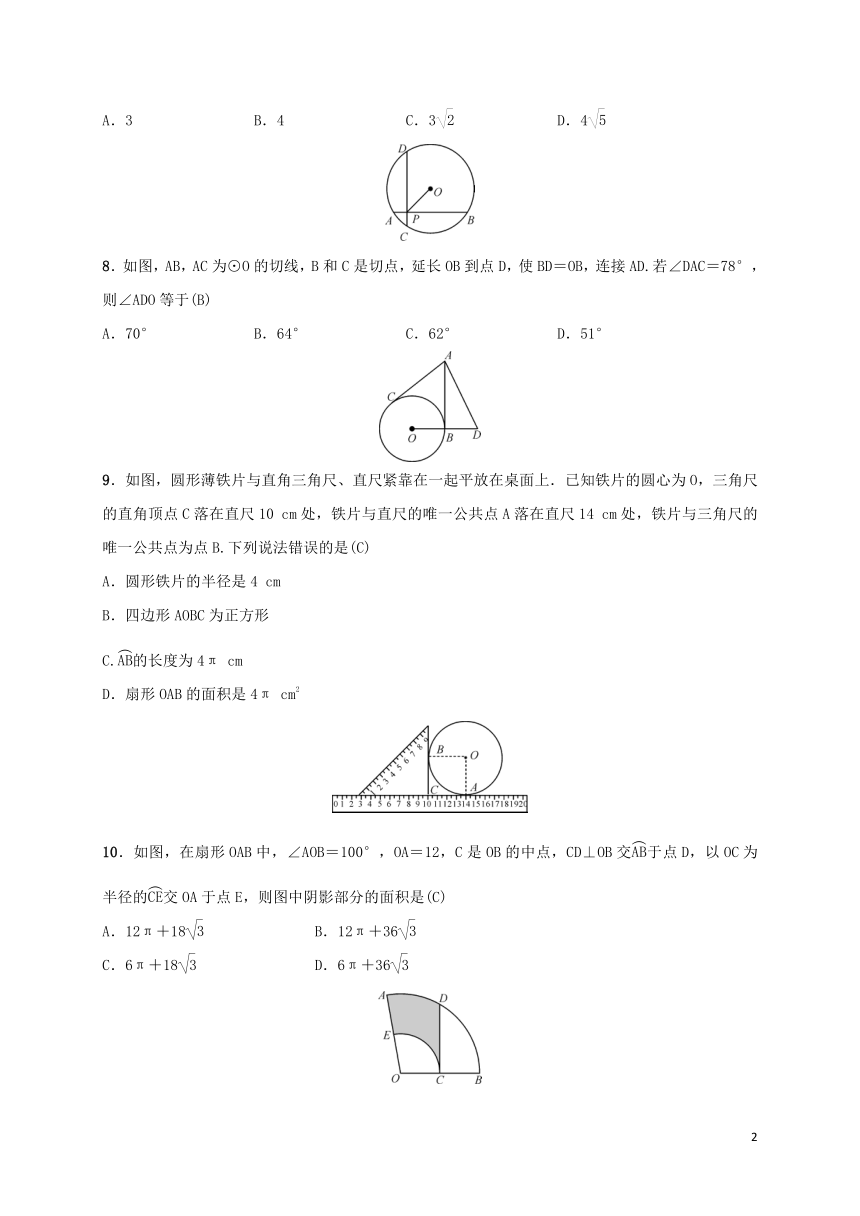
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(B)
A.70° B.60° C.50° D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(A)
A.r=R B.r=R C.r=R D.r=R
5.如图,AB是半圆的直径,AB=2,∠B=30°,则的长为(B)
A.π B.π C.π D.
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(C)
A.(2,-1) B.(2,2) C.(2,1) D.(3,1)
7.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为(C)
A.3 B.4 C.3 D.4
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.若∠DAC=78°,则∠ADO等于(B)
A.70° B.64° C.62° D.51°
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10 cm处,铁片与直尺的唯一公共点A落在直尺14 cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(C)
A.圆形铁片的半径是4 cm
B.四边形AOBC为正方形
C.的长度为4π cm
D.扇形OAB的面积是4π cm2
10.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是(C)
A.12π+18 B.12π+36
C.6π+18 D.6π+36
二、填空题(每小题4分,共24分)
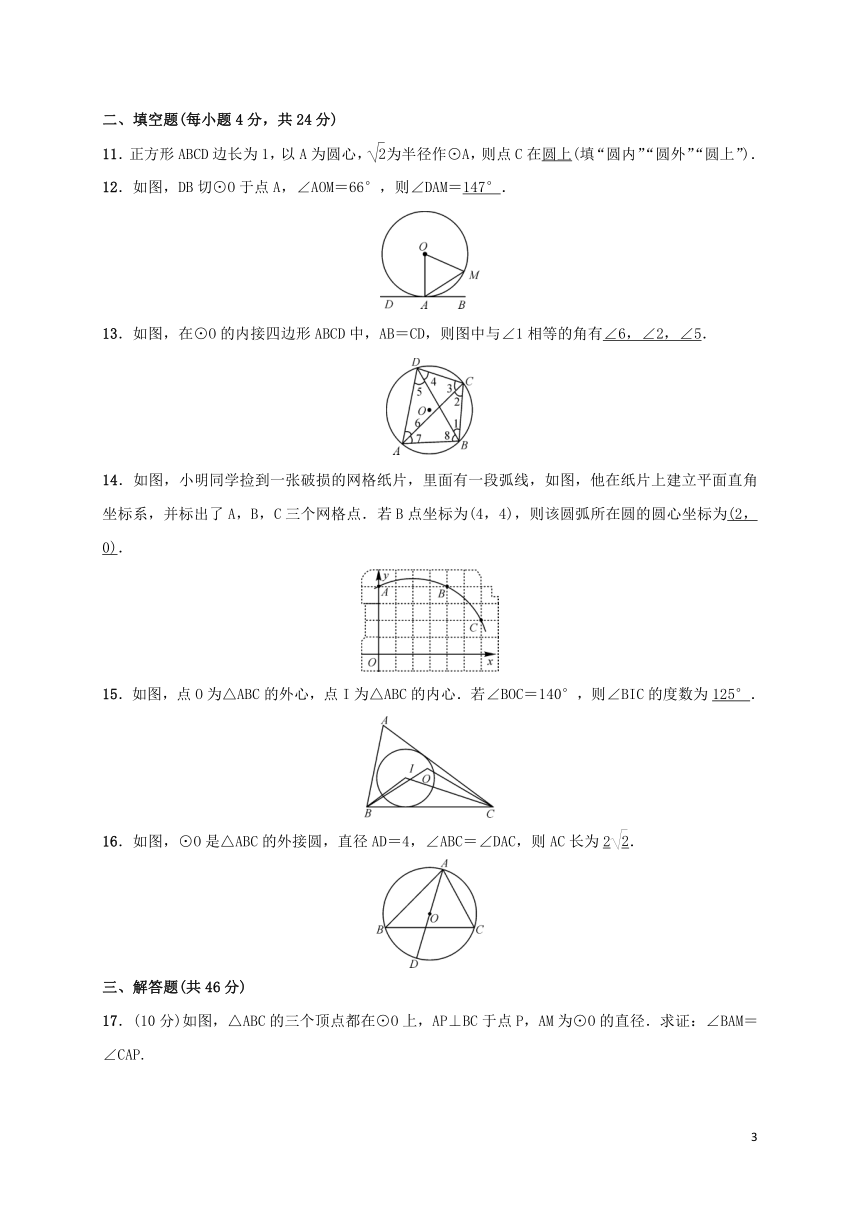
11.正方形ABCD边长为1,以A为圆心,为半径作⊙A,则点C在圆上(填“圆内”“圆外”“圆上”).
12.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=147°.
13.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有∠6,∠2,∠5.
14.如图,小明同学捡到一张破损的网格纸片,里面有一段弧线,如图,他在纸片上建立平面直角坐标系,并标出了A,B,C三个网格点.若B点坐标为(4,4),则该圆弧所在圆的圆心坐标为(2,0).
15.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为125°.
16.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为2.
三、解答题(共46分)
17.(10分)如图,△ABC的三个顶点都在⊙O上,AP⊥BC于点P,AM为⊙O的直径.求证:∠BAM=∠CAP.
证明:连接BM,
∵AP⊥BC于点P,AM为⊙O的直径,
∴∠BAM=90°-∠M,∠CAP=90°-∠C.
又∵∠M=∠C,
∴∠BAM=∠CAP.
18.(10分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
解:(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
19.(12分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)若BD=1,tan∠BAD=,求⊙O的半径.
解:(1)证明:连接OA.
∵AE为⊙O的切线,BD⊥AE,
∴∠DAO=∠EDB=90°.
∴DB∥AO.
∴∠DBA=∠BAO.
又∵OA=OB,∴∠ABC=∠BAO.
∴∠DBA=∠ABC.
(2)∵BD=1,tan∠BAD=,
∴AD=2.
∴AB==.
∴cos∠DBA=.
∵∠DBA=∠CBA,∴BC===5.
∴⊙O的半径为2.5.
20.(14分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∴∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.
∴=.∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴EB=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
一、选择题(每小题3分,共30分)
1.下列说法正确的是(B)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(C)
A.点P在⊙O上 B.点P在⊙O内
C.点P在⊙O外 D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(B)
A.70° B.60° C.50° D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(A)
A.r=R B.r=R C.r=R D.r=R
5.如图,AB是半圆的直径,AB=2,∠B=30°,则的长为(B)
A.π B.π C.π D.
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(C)
A.(2,-1) B.(2,2) C.(2,1) D.(3,1)
7.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为(C)
A.3 B.4 C.3 D.4
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.若∠DAC=78°,则∠ADO等于(B)
A.70° B.64° C.62° D.51°
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10 cm处,铁片与直尺的唯一公共点A落在直尺14 cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(C)
A.圆形铁片的半径是4 cm
B.四边形AOBC为正方形
C.的长度为4π cm
D.扇形OAB的面积是4π cm2
10.如图,在扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是(C)
A.12π+18 B.12π+36
C.6π+18 D.6π+36
二、填空题(每小题4分,共24分)
11.正方形ABCD边长为1,以A为圆心,为半径作⊙A,则点C在圆上(填“圆内”“圆外”“圆上”).
12.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=147°.
13.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有∠6,∠2,∠5.
14.如图,小明同学捡到一张破损的网格纸片,里面有一段弧线,如图,他在纸片上建立平面直角坐标系,并标出了A,B,C三个网格点.若B点坐标为(4,4),则该圆弧所在圆的圆心坐标为(2,0).
15.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为125°.
16.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为2.
三、解答题(共46分)
17.(10分)如图,△ABC的三个顶点都在⊙O上,AP⊥BC于点P,AM为⊙O的直径.求证:∠BAM=∠CAP.
证明:连接BM,
∵AP⊥BC于点P,AM为⊙O的直径,
∴∠BAM=90°-∠M,∠CAP=90°-∠C.
又∵∠M=∠C,
∴∠BAM=∠CAP.
18.(10分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
解:(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵=,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵=,∴∠AOE=60°.
∴∠EOC=60°.
∴的长为2π×(2+2)×=π.
19.(12分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)若BD=1,tan∠BAD=,求⊙O的半径.
解:(1)证明:连接OA.
∵AE为⊙O的切线,BD⊥AE,
∴∠DAO=∠EDB=90°.
∴DB∥AO.
∴∠DBA=∠BAO.
又∵OA=OB,∴∠ABC=∠BAO.
∴∠DBA=∠ABC.
(2)∵BD=1,tan∠BAD=,
∴AD=2.
∴AB==.
∴cos∠DBA=.
∵∠DBA=∠CBA,∴BC===5.
∴⊙O的半径为2.5.
20.(14分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∴∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.
∴=.∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴EB=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
